Conjunto preordenado
En matemática, especialmente en teoría del orden, preórdenes son ciertas clases de relaciones binarias que se relacionan con los conjuntos parcialmente ordenados. El nombre cuasiorden es también una expresión común para preórdenes. Muchas definiciones teóricas para los conjuntos parcialmente ordenados se pueden generalizar a preórdenes, pero el esfuerzo adicional de generalización raramente se necesita. Con todo hay campos de uso, tales como la definición de la convergencia vía redes en topología, donde los preórdenes no se pueden substituir por conjuntos parcialmente ordenados sin perder propiedades importantes.
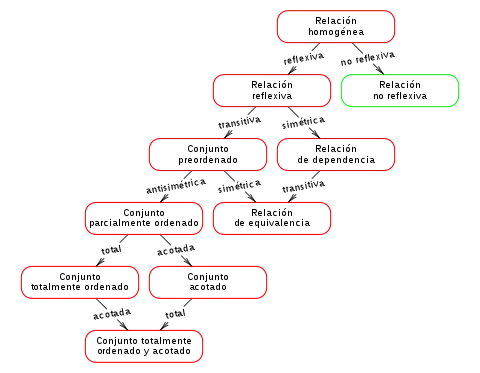
Definición formal
Considere algún conjunto P y una relación binaria R en P. Entonces R es un preorden, o un cuasiorden, si es reflexiva y transitiva, es decir, para todo a, b y c en P, tenemos que:
Es un conjunto preordenado, si cumple:
1.- La relación R es reflexiva si todo elemento a de P está relacionado consigo mismo.
2.- La relación R es transitiva si un elemento a está relacionado con otro b, y este b con otro c, entonces el elemento a esta también relacionado con el c.
Entonces en una relación binaria de preorden.
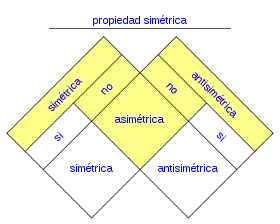
Si un preorden cumple también la propiedad simétrica para todo a, b de P, si a R b entonces b R a, (P, R) es una relación de equivalencia
Si un preorden cumple también la propiedad antisimétrica, es decir, a R b y b R a implica a = b, entonces (P, R) es un orden parcial.
Es importante diferenciar las siguientes tres propiedades:
- La relación R es simétrica si un elemento a está relacionado con otro b, entonces el b también está relacionado con el a.
Para todo a, b de P, si se cumple que a esta relacionada con b entonces b esta relacionada con a.
- La relación R es antisimétrica si un elemento a está relacionado con otro b, entonces el b no está relacionado con el a.
Para todo a, b de P, si se cumple que a esta relacionada con b entonces b no esta relacionada con a.
- La relación R es asimétrica si no cumple ninguna de las dos condiciones anteriores.
Ejemplo
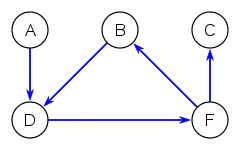

Un grafo dirigido, que tiene al menos un ciclo, es preordenado dado que cumple la propiedad reflexiva y transitiva, y no es ni simétrico ni antisimétrico.
Orden parcial asociado
Dado un preorden en un conjunto , se puede definir la relación de equivalencia para . El preorden genera una relación de orden en el conjunto cociente dada por para , que está bien definida ( denota la clase de para ).
También se puede hacer el proceso inverso: dada una partición de , un orden parcial en el ella determina un preorden en .