Red neuronal artificial
Las redes neuronales artificiales (también conocidas como sistemas conexionistas) son un modelo computacional evolucionado a partir de diversas aportaciones científicas que están registradas en la historia.[1] Consiste en un conjunto de unidades, llamadas neuronas artificiales, conectadas entre sí para transmitirse señales. La información de entrada atraviesa la red neuronal (donde se somete a diversas operaciones) produciendo unos valores de salida.
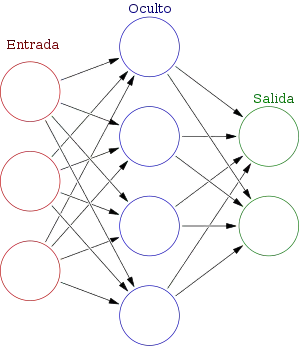
Cada neurona está conectada con otras a través de unos enlaces. En estos enlaces el valor de salida de la neurona anterior es multiplicado por un valor de peso. Estos pesos en los enlaces pueden incrementar o inhibir el estado de activación de las neuronas adyacentes. Del mismo modo, a la salida de la neurona, puede existir una función limitadora o umbral, que modifica el valor resultado o impone un límite que no se debe sobrepasar antes de propagarse a otra neurona. Esta función se conoce como función de activación.
Estos sistemas aprenden y se forman a sí mismos, en lugar de ser programados de forma explícita, y sobresalen en áreas donde la detección de soluciones o características es difícil de expresar con la programación convencional. Para realizar este aprendizaje automático, normalmente, se intenta minimizar una función de pérdida que evalúa la red en su total. Los valores de los pesos de las neuronas se van actualizando buscando reducir el valor de la función de pérdida. Este proceso se realiza mediante la propagación hacia atrás.
El objetivo de la red neuronal es resolver los problemas de la misma manera que el cerebro humano, aunque las redes neuronales son más abstractas. Las redes neuronales actuales suelen contener desde unos miles a unos pocos millones de unidades neuronales.
Nuevas investigaciones sobre el cerebro a menudo estimulan la creación de nuevos patrones en las redes neuronales. Un nuevo enfoque está utilizando conexiones que se extienden mucho más allá y capas de procesamiento de enlace en lugar de estar siempre localizado en las neuronas adyacentes. Otra investigación está estudiando los diferentes tipos de señal en el tiempo que los axones se propagan, como el aprendizaje profundo, interpola una mayor complejidad que un conjunto de variables booleanas que son simplemente encendido o apagado.
Las redes neuronales se han utilizado para resolver una amplia variedad de tareas, como la visión por computador y el reconocimiento de voz, que son difíciles de resolver usando la ordinaria programación basado en reglas. Históricamente, el uso de modelos de redes neuronales marcó un cambio de dirección a finales de los años ochenta de alto nivel, que se caracteriza por sistemas expertos con conocimiento incorporado en si-entonces las reglas, a bajo nivel de aprendizaje automático, caracterizado por el conocimiento incorporado en los parámetros de un modelo cognitivo con algún sistema dinámico.
Historia
Warren McCulloch y Walter Pitts [2] (1943) crearon un modelo informático para redes neuronales, que se llama lógica umbral, que se basa en las matemáticas y los algoritmos. Este modelo señaló el camino para que la investigación de redes neuronales se divida en dos enfoques distintos. Un enfoque se centró en los procesos biológicos en el cerebro y el otro se centró en la aplicación de redes neuronales para la inteligencia artificial.
Aprendizaje de Hebb
A finales de la década de 1940 el psicólogo Donald Hebb[3][4] creó una hipótesis de aprendizaje basado en el mecanismo de plasticidad neuronal que ahora se conoce como aprendizaje de Hebb. Aprendizaje de Hebb se considera que es un "típico" de aprendizaje no supervisado y sus variantes posteriores fueron los primeros modelos de la potenciación a largo plazo. Los investigadores empezaron a aplicar estas ideas a los modelos computacionales en 1948 con la sugerencia de Turing, que el córtex humano infantil es lo que llamaba "máquina desorganizada" (también conocido como "máquina Turing Tipo B").[5][6]
Farley y Wesley A. Clark[7] (1954) al principio utilizaron máquinas computacionales, que entonces se llamaban "calculadoras", para simular una red de Hebb en el MIT. Otras simulaciones de redes neuronales por computadora han sido creadas por Rochester, Holland, Habit y Duda (1956).[8]
Frank Rosenblatt[9][10] (1958) creó el perceptrón, un algoritmo de reconocimiento de patrones basado en una red de aprendizaje de computadora de dos capas, que utilizaba adición y sustracción simples. Con la notación matemática, Rosenblatt también describe circuitería que no está en el perceptrón básico, tal como el circuito de o-exclusiva, un circuito que no se pudo procesar por redes neuronales antes de la creación del algoritmo de propagación hacia atrás por Paul Werbos (1975).[11]
En 1959, un modelo biológico propuesto por dos laureados de los Premios Nobel, David H. Hubel y Torsten Wiesel, estaba basado en su descubrimiento de dos tipos de células en la corteza visual primaria: células simples y células complejas.[12]
El primer reporte sobre redes funcionales multicapas fue publicado en 1965 por Ivakhnenko y Lapa, y se conoce como el método de agrupamiento para el manejo de datos.[13][14][15]
La investigación de redes neuronales se estancó después de la publicación de la investigación de aprendizaje automático por Marvin Minsky y Seymour Papert (1969),[16] que descubrió dos cuestiones fundamentales con las máquinas computacionales que procesan las redes neuronales. La primera fue que los perceptrones básicos eran incapaces de procesar el circuito de o-exclusivo. La segunda cuestión importante era que los ordenadores no tenían suficiente poder de procesamiento para manejar eficazmente el gran tiempo de ejecución requerido por las grandes redes neuronales.
Propagación hacia atrás y el resurgimiento
Un avance clave posterior fue el algoritmo de propagación hacia atrás que resuelve eficazmente el problema de o-exclusivo, y en general el problema de la formación rápida de redes neuronales de múltiples capas (Werbos 1975). El proceso de propagación hacia atrás utiliza la diferencia entre el resultado producido y el resultado deseado para cambiar los "pesos" de las conexiones entre las neuronas artificiales.[11]
A mediados de la década de 1980, el procesamiento distribuido en paralelo se hizo popular con el nombre conexionismo. El libro de David E. Rumelhart y James McClelland (1986) proporcionan una exposición completa de la utilización de conexionismo en los ordenadores para simular procesos neuronales.[17]
Las redes neuronales, tal como se utilizan en la inteligencia artificial, han sido consideradas tradicionalmente como modelos simplificados de procesamiento neuronal en el cerebro, a pesar de que la relación entre este modelo y la arquitectura biológica del cerebro se debate; no está claro en qué medida las redes neuronales artificiales reflejan el funcionamiento cerebral.
Máquinas de soporte vectorial y otros métodos mucho más simples, tales como los clasificadores lineales, alcanzaron gradualmente popularidad en el aprendizaje automático. No obstante, el uso de redes neuronales ha cambiado algunos campos, tales como la predicción de las estructuras de las proteínas.[18][19]
En 1992,fue introducido el max-pooling (una forma de submuestreo, en la que se divide los datos en grupos de tamaños iguales, que no tienen elementos en común, y se transmite solamente el valor máximo de cada grupo)para ayudar con el reconocimiento de objetos tri-dimensionales.[20] [21] [22]
En 2010, el uso de max-pooling en la formación por propagación hacia atrás fue acelerado por los GPUs, y se demostró que ofrece mejor rendimiento que otros tipos de agrupamiento.[23]
El problema del desvanecimiento del gradiente afecta las redes neuronales prealimentadas de múltiples capas, que usan la propagación hacia atrás, y también los redes neuronales recurrentes (RNNs).[24][25] Aunque los errores se propagan de una capa a otra, disminuyen exponencialmente con el número de capas, y eso impide el ajuste hacia atrás de los pesos de las neuronas basado en esos errores. Las redes profundas se ven particularmente afectadas.
Para vencer este problema, Schmidhuber adoptaba una jerarquía multicapa de redes (1992) preformados, una capa a la vez, por aprendizaje no supervisado, y refinado por propagación hacia atrás.[26] Behnke (2003) contaba solamente con el signo del gradiente (Rprop)[27] tratándose de problemas tales como la reconstrucción de imágenes y la localización de caras.
Como retos anteriores en redes neuronales profundas de capacitación se resolvieron con métodos como preformación no supervisada y potencia de cálculo incrementada a través del uso de las GPU y la computación distribuida, las redes neuronales se desplegaron de nuevo a gran escala, sobre todo en problemas de procesamiento de imágenes y de reconocimiento visual. Esto se conoció como "aprendizaje profundo", aunque el aprendizaje profundo no es estrictamente sinónimo de redes neuronales profundas.
Diseños basados en hardware
Se crearon en CMOS dispositivos de cómputo para la simulación biofísica al igual que para la cómputo neuromórfico. Nanodispositivos[28] para análisis de componentes principales de escala muy grande y convolución pueden crear una clase nueva de cómputo neuronal, porque son fundamentalmente analógicos en vez de digitales (aunque las primeras implementaciones puedan utilizar dispositivos digitales).[29] Ciresan y sus cólegos (2010)[30] en el grupo de Schmidhuber mostraron que, a pesar del problema del desvanecimiento del gradiente, los GPUs hacen factible la propagación hacia atrás para las redes neuronales prealimentadas con múltiples capas.
Mejoras desde 2006
Se han creado dispositivos computacionales en el CMOS, tanto para la simulación biofísica como para computación neuromórfica. Los esfuerzos más recientes se muestran prometedores para la creación de nanodispositivos[31] para análisis de componentes principales de gran escala. Si tiene éxito, se crearía una nueva clase de computación neuronal, ya que depende de aprendizaje automático en lugar de la programación y porque es fundamentalmente analógico en lugar de digital a pesar de que las primeras instancias pueden ser de hecho con los dispositivos digitales CMOS.[32]
Entre 2009 y 2012, las redes neuronales recurrentes y redes neuronales profundas feedforward desarrollados en el grupo de investigación de Jürgen Schmidhuber en el laboratorio suizo de IA IDSIA han ganado ocho concursos internacionales de reconocimiento de patrones y aprendizaje automático. Por ejemplo, la memoria bidireccional y multidimensional de largo a corto plazo (LSTM) de Alex Graves ha ganado tres competiciones en el reconocimiento de escritura conectada en Conferencia Internacional sobre Análisis de documentos y Reconocimiento (ICDAR) del 2009, sin ningún conocimiento previo acerca de los tres idiomas diferentes que se pueden aprender.
Implementaciones de este método basadas en unidades de procesamiento gráfico rápidas, hechos por Dan Ciresan y sus colegas de IDSIA han ganado varios concursos de reconocimiento de patrones, incluyendo la Competición de Reconocimiento de Señales de Tráfico del 2011,[33] el desafío de ISBI 2012 de segmentación de estructuras neuronales en series de imágenes de Microscopía Electrónica,[34] y otros. Sus redes neuronales también fueron las primeras reconocedoras artificiales de patrones en lograr un rendimiento superior al humano en los puntos de referencia importantes, tales como el reconocimiento de señales de tráfico (IJCNN 2012) o el problema de clasificación de dígitos escritos a mano.
Arquitecturas profundas altamente no lineales similares a las del 1980 Neocognitrón por Kunihiko Fukushima y la "arquitectura estándar de la visión", inspirados en las células simples y complejas identificadas por David H. Hubel y Torsten Wiesel en la corteza visual, pueden también ser preformados por métodos no supervisados en el laboratorio de la universidad de Toronto. Un equipo de este laboratorio ganó un concurso en 2012 patrocinado por Merck para el diseño de software para ayudar a encontrar moléculas que podrían conducir a nuevos medicamentos.
Modelos
Los modelos de redes neuronales en la inteligencia artificial se refieren generalmente a las redes neuronales artificiales (RNA); estos son modelos matemáticos esencialmente simples que definen una función f:X→Y o una distribución más X o ambos X e Y. Pero a veces los modelos también están íntimamente asociadas con un algoritmo de aprendizaje en particular o regla de aprendizaje. Un uso común de la frase "modelo ANN" es en realidad la definición de una clase de tales funciones (donde los miembros de la clase se obtiene variando parámetros, los pesos de conexión, o específicos de la arquitectura, tales como el número de neuronas o su conectividad).
Función de red
La palabra red en el término "red neuronal artificial" se refiere a las interconexiones entre las neuronas en las diferentes capas de cada sistema. Un sistema ejemplar tiene tres capas. La primera capa tiene neuronas de entrada que envían datos a través de las sinapsis a la segunda capa de neuronas, y luego a través de más sinapsis a la tercera capa de neuronas de salida. Los sistemas más complejos tendrán más capas, algunos aumentando las de entrada y de salida de neuronas. Las sinapsis almacenan parámetros llamados "pesos" que manipulan los datos en los cálculos.
Un RNA se define típicamente por tres tipos de parámetros:
1. El patrón de interconexión entre las diferentes capas de neuronas
2. El proceso de aprendizaje para la actualización de los pesos de las interconexiones
3. La función de activación que convierte las entradas ponderadas de una neurona a su activación a la salida.
Matemáticamente, la función de red de una neurona se define como una composición de otras funciones . Este se representa como una estructura de red, con flechas que representan las dependencias entre variables. Un tipo ampliamente utilizado de la composición es la suma ponderada no lineal , donde, dónde k (denominado comúnmente como la función de activación[35]) es una función predefinida, como la tangente hiperbólica o función sigmoide . La característica importante de la función de activación es que proporciona una transición suave como valores de entrada de cambio, es decir, un pequeño cambio en la entrada produce un pequeño cambio en la producción. Será conveniente para la siguiente para referirse a una colección de funciones simplemente como un vector .
Esta cifra representa una descomposición de tales , Con las dependencias entre las variables indicadas por las flechas. Estos pueden ser interpretados de dos maneras.
La primera vista es la vista funcional: la entrada se transforma en un vector de 3 dimensiones , Que se transforma a continuación en un vector de 2 dimensiones , Que es finalmente transformado en . Este punto de vista se encuentra más comúnmente en el contexto de la optimización.
El segundo punto de vista es la vista probabilístico: la variable aleatoria depende de la variable aleatoria , Que depende de , Que depende de la variable aleatoria . Este punto de vista se encuentra más comúnmente en el contexto de modelos gráficos .
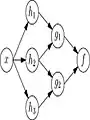
Los dos puntos de vista son en gran medida equivalente. En cualquier caso, para esta arquitectura de red en particular, los componentes de las capas individuales son independientes entre sí (por ejemplo, los componentes de son independientes entre sí, dada su aportación ). Esto permite, naturalmente, un grado de paralelismo en la ejecución.
Las redes como la anterior se llaman comúnmente alimentación hacia delante , porque su gráfica es un grafo dirigido acíclico . Las redes con ciclos se denominan comúnmente recurrentes . Tales redes se representan comúnmente de la manera mostrada en la parte superior de la figura, donde se muestra como dependiente sobre sí misma. Sin embargo, no se muestra una dependencia temporal implícita.
El aprendizaje
Lo que ha atraído el mayor interés en las redes neuronales es la posibilidad de aprendizaje. Dada una determinada tarea a resolver, y una clase de funciones , el aprendizaje consiste en utilizar un conjunto de observaciones para encontrar la cual resuelve la tarea de alguna forma óptima.
Esto implica la definición de una función de coste tal que, para la solución óptima . Es decir, ninguna solución tiene un costo menor que el costo de la solución óptima.
La función de coste es un concepto importante en el aprendizaje, ya que representa lo lejos que una solución particular se encuentra de la solución óptima al problema a resolver. Los algoritmos de aprendizaje buscan a través del espacio de soluciones para encontrar una función que tiene el menor costo posible.
Para aplicaciones en las que la solución es dependiente de algunos datos, el costo debe ser necesariamente una función de las observaciones, de lo contrario no estaríamos modelando todo lo relacionado con los datos. Con frecuencia se define como una estadística a la que se pueden realizar sólo aproximaciones. Como un simple ejemplo, considere el problema de encontrar el modelo , Lo que reduce al mínimo , Para pares de datos extraída de alguna distribución . En situaciones prácticas sólo tendríamos muestras de y, por tanto, para el ejemplo anterior, tendríamos solamente minimizar . Por lo tanto, el coste se reduce al mínimo a través de una muestra de los datos en lugar de toda la distribución de la generación de los datos.
Cuando alguna forma de aprendizaje automático en línea debe ser utilizada, donde el costo se reduce al mínimo parcialmente como se ve cada nuevo ejemplo. Mientras que la máquina de aprendizaje en línea se utiliza a menudo cuando se fija, es más útil en el caso en el que la distribución cambia lentamente con el tiempo. En los métodos de redes neuronales, alguna forma de aprendizaje en línea de la máquina se utiliza con frecuencia para conjuntos de datos finitos.
La elección de una función de coste
Si bien es posible definir alguna función de coste, con frecuencia un coste particular, se utilizará, ya sea porque tiene propiedades deseables (tales como convexidad) o porque surge de forma natural a partir de una formulación particular del problema (por ejemplo, en una formulación probabilística la probabilidad posterior del modelo puede ser utilizada como un costo inverso). En última instancia, la función de coste dependerá de la tarea deseada.
Paradigmas de aprendizaje
Hay tres grandes paradigmas de aprendizaje, cada uno correspondiente a una tarea de aprendizaje abstracto en particular. Estos son el aprendizaje supervisado ,el aprendizaje no supervisado y el aprendizaje por refuerzo.
El aprendizaje supervisado
En el aprendizaje supervisado, se nos da una serie de ejemplos de pares y el objetivo es encontrar una función en la clase permitido de funciones que corresponden con los ejemplos. En otras palabras, deseamos inferir el mapeo derivado de los datos; la función de coste está relacionado con la falta de coincidencia entre nuestro mapeo y los datos, y contiene implícitamente el conocimiento previo sobre el dominio del problema.[36]
Un coste de uso común es el error cuadrático medio, que trata de minimizar el error cuadrático medio entre las salidas de la red, y el valor objetivo sobre todos los pares ejemplares. Cuando uno trata de minimizar este coste utilizando descenso de gradiente para la clase de las redes neuronales llamadas perceptrones multicapas (MLP), se obtiene el común y bien conocido algoritmo de propagación hacia atrás para la formación de redes neuronales.
Tareas que caen dentro del paradigma de aprendizaje supervisado son el reconocimiento de patrones (también conocido como clasificación) y regresión (también conocido como aproximación de función). El paradigma de aprendizaje supervisado es aplicable también a los datos secuenciales (por ejemplo, reconocimiento del habla, del manuscrito, y de gestos). Esto se puede considerar como una forma de aprendizaje con un "maestro", en la forma de una función que proporciona información continua sobre la calidad de las soluciones obtenidas hasta el momento.
Aprendizaje no supervisado
En el aprendizaje no supervisado, algunos datos se da y la función de coste que se reduce al mínimo, que puede ser cualquier función de los datos y la salida de la red, .
La función de coste depende de la tarea (lo que estamos tratando de modelar) y nuestros a priori suposiciones implícitas (las propiedades de nuestro modelo, sus parámetros y las variables observadas).
Como un ejemplo trivial, considere el modelo donde es una constante y el costo . Minimizar este coste nos dará un valor de que es igual a la media de los datos. La función de coste puede ser mucho más complicado. Su forma depende de la aplicación: por ejemplo, en la compresión de que podría estar relacionado con la información mutua entre y , Mientras que en la modelización estadística, que podría estar relacionado con la probabilidad posterior del modelo dados los datos (tenga en cuenta que en estos dos ejemplos esas cantidades se maximizaría en lugar de reducirse al mínimo).
Tareas que caen dentro del paradigma de aprendizaje no supervisado están en generales de estimación de problemas; las aplicaciones incluyen el agrupamiento, la estimación de distribuciones estadísticas, la compresión de datos y el filtrado bayesiano de spam.
Aprendizaje por refuerzo
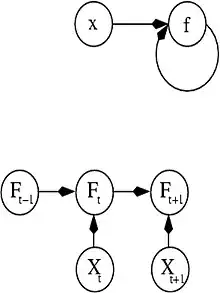
En el aprendizaje por refuerzo, los datos por lo general no se dan, pero generada por la interacción de un agente con el medio ambiente. En cada punto en el tiempo , El agente realiza una acción y el medio ambiente genera una observación y un costo instantáneo , De acuerdo con algunas dinámicas (por lo general desconocidos). El objetivo es descubrir una política para la selección de las acciones que minimiza una cierta medida de un costo a largo plazo, por ejemplo, el coste acumulativo esperado. La dinámica del medio ambiente y el coste a largo plazo para cada política general son desconocidos, pero pueden ser estimados.
Más formalmente el medio ambiente se modela como un proceso de decisión de Markov (MDP) con los estados y acciones con las siguientes distribuciones de probabilidad: la distribución de costos instantánea ,La distribución de observación y la transición Mientras que una política se define como la distribución condicional sobre las acciones dadas las observaciones. Tomados en conjunto, los dos entonces definen una cadena de Márkov (MC). El objetivo es descubrir la política (es decir, el MC) que minimice el costo.
RNAs se utilizan con frecuencia en el aprendizaje de refuerzo como parte del algoritmo general.[37][38] La programación dinámica se ha unido a las RNA (dando la programación neurodinámica) por Bertsekas y Tsitsiklis[39] y se aplicó problemas no lineales a la multi-dimensionales, tales como los implicados en enrutamiento de vehículos , gestión de los recursos naturales[40][41] o la medicina[42] debido a la capacidad de RNAs para mitigar las pérdidas de precisión incluso cuando la reducción de la densidad de la red de discretización para aproximar numéricamente la solución de los problemas de control originales.
Tareas que caen dentro del paradigma de aprendizaje por refuerzo son problemas de control, juegos y otras secuenciales tareas.
Tipo de entrada
Finalmente las RNAs también se pueden clasificar según sean capaces de procesar información de distinto tipo en:
- Redes analógicas: procesan datos de entrada con valores continuos y, habitualmente, acotados. Ejemplos de este tipo de redes son: Hopfield, Kohonen y las redes de aprendizaje competitivo.
- Redes discretas: procesan datos de entrada de naturaleza discreta; habitualmente valores lógicos booleanos. Ejemplos de este segundo tipo de redes son: las máquinas de Boltzmann y Cauchy, y la red discreta de Hopfield.
Algoritmos de aprendizaje
La formación de un modelo de red neuronal en esencia significa seleccionar un modelo de la serie de modelos permitidos (o, en un bayesiano marco, la determinación de una distribución en el conjunto de modelos permitidos) que minimiza el criterio de costo. Hay numerosos algoritmos disponibles para la formación de los modelos de redes neuronales; la mayoría de ellos puede ser vista como una aplicación directa de la teoría de optimización y la estimación estadística.
La mayoría de los algoritmos utilizados en las redes neuronales artificiales de formación emplean alguna forma de descenso de gradiente, utilizando propagación hacia atrás para calcular los gradientes reales. Esto se hace simplemente tomando la derivada de la función de coste con respecto a los parámetros de la red y a continuación, cambiando los parámetros en una dirección relacionada al gradiente. Los algoritmos de formación de propagación hacia atrás generalmente se clasifican en tres categorías:
Descenso del gradiente (con tasa variable de aprendizaje y momentum, retropropagación elástica (Rprop));
- cuasi-Newton ( Broyden-Fletcher-Goldfarb-Shannon, Método de la secante );
- Levenberg-Marquardt y gradiente conjugado (actualización Fletcher-Reeves, actualizaación Polak-Ribiere, Powell-Beale reinicio, gradiente conjugado escalado).[43]
Métodos evolutivos,[44] de programación de la expresión génica,[45] de recocido simulado,[46] de esperanza-maximización, los métodos no paramétricos y la optimización por enjambre de partículas[47] son algunos otros métodos para la formación de redes neuronales.
Algoritmo recursivo convergente de aprendizaje
Este es un método de aprendizaje específicamente desegnado para redes neuronales controladores de articulación (CMAC por sus siglas en inglés) de modelo cerebelosa. En 2004, un algoritmo recursivo de mínimos cuadrados estaba introducido para formar en línea redes neuronales CMAC. [48] Este algoritmo puede convergir en un solo paso, y actualizar todos los pesos en un solo paso con cualquier dato nuevo de entrada. Al principio, este algoritmo tenía complejidad computacional de O(N3). Basado en factorización QR, este algoritmo recursivo de aprendizaje había sido simplificado para hacerlo O(N).[49]
El empleo de redes neuronales artificiales
Tal vez la mayor ventaja de las RNA es su capacidad de ser utilizado como un mecanismo de función de aproximación arbitraria que "aprende" a partir de datos observados. Sin embargo, su uso no es tan sencillo, y una relativamente buena comprensión de la teoría subyacente es esencial.
- Elección de modelo
- Esto dependerá de la representación de datos y la aplicación. Excesivamente complejos modelos tienden a conducir a problemas en el aprendizaje.
- Algoritmo de aprendizaje
- Existen numerosas soluciones de compromiso entre los algoritmos de aprendizaje. Casi cualquier algoritmo va a funcionar bien con los hiperparámetros correctos para la formación de un conjunto específico de datos fijos. Sin embargo, la selección y el ajuste de un algoritmo para la formación en datos no previstos requieren una cantidad significativa de experimentación.
- Robustez
- Si se seleccionan apropiadamente el modelo, la función de coste y el algoritmo de aprendizaje, la RNA resultante puede ser extremadamente robusta.
Con la aplicación correcta, las RNA pueden ser utilizadas de forma natural en el aprendizaje online y aplicaciones de grandes conjuntos de datos. Su aplicación sencilla y la existencia de dependencias en su mayoría locales expuestos en la estructura permiten implementaciones rápidas y paralelas en el hardware.
Aplicaciones
RNA las hacen bastante apropiadas para aplicaciones en las que no se dispone a priori de un modelo identificable que pueda ser programado, pero se dispone de un conjunto básico de ejemplos de entrada (previamente clasificados o no). Asimismo, son altamente robustas tanto al ruido como a la disfunción de elementos concretos y son fácilmente paralelizables.
Esto incluye problemas de clasificación y reconocimiento de patrones de voz, imágenes, señales, etc. Asimismo se han utilizado para encontrar patrones de fraude económico, hacer predicciones en el mercado financiero, hacer predicciones de tiempo atmosférico, etc.
También se pueden utilizar cuando no existen modelos matemáticos precisos o algoritmos con complejidad razonable, por ejemplo la red de Kohonen ha sido aplicada con un éxito más que razonable al clásico problema del viajante (un problema para el que no se conoce solución algorítmica de complejidad polinómica).
Otro tipo especial de redes neuronales artificiales se ha aplicado en conjunción con los algoritmos genéticos (AG) para crear controladores para robots. La disciplina que trata la evolución de redes neuronales mediante algoritmos genéticos se denomina Robótica Evolutiva. En este tipo de aplicación el genoma del AG lo constituyen los parámetros de la red (topología, algoritmo de aprendizaje, funciones de activación, etc.) y la adecuación de la red viene dada por la adecuación del comportamiento exhibido por el robot controlado (normalmente una simulación de dicho comportamiento).
Aplicaciones de la vida real
Las tareas se aplican a las redes neuronales artificiales tienden a caer dentro de las siguientes categorías generales:
- Aproximación de funciones, o el análisis de regresión, incluyendo la predicción de series temporales, funciónes de aptitud y el modelado.
- Clasificación, incluyendo el reconocimiento de patrones y la secuencia de reconocimiento, detección y de la toma de decisiones secuenciales.
- Procesamiento de datos, incluyendo el filtrado, el agrupamiento, la separación ciega de las señales y compresión.
- Robótica, incluyendo la dirección de manipuladores y prótesis.
- Ingeniería de control, incluyendo control numérico por computadora.
Las áreas de aplicación incluyen la identificación de sistemas y el control (control del vehículo, predicción de trayectorias,[50] el control de procesos, manejo de recursos naturales), la química cuántica, juegos y la toma de decisiones (backgammon, ajedrez, póquer ), el reconocimiento de patrones (sistemas radar, reconocimiento facial, clasificación de señales,[51] reconocimiento de objetos y más), de reconocimiento de secuencia (gesto, voz, reconocimiento de texto escrito a mano), diagnóstico médico , aplicaciones económico-financieras (por ejemplo, sistemas automatizados para el comercio en varios sectores de actividad), minería de datos (o descubrimiento de conocimiento en bases de datos, "KDD"), la visualización, traducción automática, diferenciando entre informes deseados y no deseados en redes sociales,[52] prevención de spam (correo basura) de correo electrónico.
Las redes neuronales artificiales se han utilizado también para el diagnóstico de varios tipos de cáncer. Un sistema de detección de cáncer de pulmón híbrido basado ANN llamado HLND mejora la precisión del diagnóstico y la velocidad de la radiología cáncer de pulmón. Estas redes también se han utilizado para diagnosticar el cáncer de próstata. Los diagnósticos se pueden utilizar para hacer modelos específicos tomados de un gran grupo de pacientes en comparación con la información de un paciente dado. Los modelos no dependen de suposiciones acerca de las correlaciones de diferentes variables. El cáncer color rectal también se ha previsto el uso de las redes neuronales. Las redes neuronales podrían predecir el resultado de un paciente con cáncer color rectal con más precisión que los métodos clínicos actuales. Después de la formación, las redes podrían predecir múltiples resultados de los pacientes de instituciones relacionadas.
Las redes neuronales y la neurociencia
La Neurociencia Teórica y computacional son el ámbito en que se trata del análisis teórico y el modelado computacional de sistemas neuronales biológicos. Dado que los sistemas neurales están íntimamente relacionados con los procesos cognitivos y de comportamiento, el campo está muy relacionado con el modelado cognitivo y conductual.
El objetivo del campo es la creación de modelos de sistemas neuronales biológicas con el fin de comprender cómo funcionan los sistemas biológicos. Para ganar este entendimiento, los neurólogos se esfuerzan por hacer un vínculo entre los procesos biológicos observados (datos), biológicamente plausibles mecanismos para el procesamiento neuronal y aprendizaje ( redes neuronales biológicas modelos) y la teoría (la teoría del aprendizaje estadístico y la teoría de la información).
Tipos de modelos
Muchos modelos se utilizan en el campo, que se define en diferentes niveles de abstracción y el modelado de diferentes aspectos de los sistemas neurales. Se extienden desde modelos del comportamiento a corto plazo de las neuronas individuales, tras los modelos del surgimiento de la dinámica de los circuitos neuronales de la interacción entre las neuronas individuales hasta, finalmente, los modelos del surgimiento del comportamiento de los módulos neuronales abstractos que representan subsistemas completas. Estos incluyen modelos de plasticidad de largo y corto plazo, y de los sistemas neuronales y sus relaciones con el aprendizaje y la memoria de la neurona individual a nivel del sistema.
Las redes con memoria
La integración de los componentes de memoria externa con redes neuronales artificiales tiene una larga historia que se remonta a las primeras investigaciones en las representaciones distribuidas y mapas de auto-organización . Por ejemplo, en memoria distribuida dispersa los patrones codificados por las redes neuronales se utilizan como direcciones de memoria para la memoria de contenido direccionable, con "neuronas" que sirven esencialmente como dirección codificadores y decodificadores .
Más recientemente aprendizaje profundo ha demostrado ser útil en hashing semántica , donde un profundo modelo gráfico de los vectores de palabra de recuento de se obtiene a partir de un gran conjunto de documentos. Los documentos se asignan a las direcciones de memoria de tal manera que los documentos semánticamente similares se encuentran en direcciones cercanas. Documentos similares a un documento de consulta a continuación, se pueden encontrar simplemente accediendo a todas las direcciones que difieren por solo unos pocos bits de la dirección del documento de consulta.
Redes de memoria es otra extensión de las redes neuronales que incorporan la memoria a largo plazo que fue desarrollado por Facebook investigación. [53] La memoria a largo plazo puede ser leído y escrito para, con el objetivo de utilizarlo para la predicción. Estos modelos se han aplicado en el contexto de la búsqueda de respuestas (QA), donde la memoria a largo plazo que de hecho actúa como un (dinámico) base de conocimientos, y la salida es una respuesta textual.
Máquinas de Turing neuronales desarrollados por Google DeepMind permiten ampliar las capacidades de las redes neuronales profundas mediante el acoplamiento a los recursos de memoria externos, que pueden interactuar con los procesos atencionales. El sistema combinado es análogo a una máquina de Turing pero es diferenciable de extremo a extremo, lo que le permite ser formado de manera eficiente con descenso del gradiente. Los resultados preliminares demuestran que las máquinas de Turing neuronales puede deducir algoritmos simples, tales como copiar, clasificar, y recuerdo asociativo a partir de ejemplos de entrada y salida.
Computadoras neuronales diferenciables (DNC) son una extensión de las máquinas de Turing neuronal, también de DeepMind. Se han realizado fuera de las máquinas de Turing neuronales, la memoria de largo a corto plazo los sistemas y redes de la memoria en las tareas de procesamiento de secuencia.
Software de red neuronal
Software de la red neuronal se utiliza para simular, investigación , desarrollo y aplicación de redes neuronales artificiales, redes neuronales biológicas y, en algunos casos, una gama más amplia de sistemas adaptativos.
Tipos de redes neuronales artificiales
Tipos de redes neuronales artificiales varían de aquellos con sólo una o dos capas de lógica única dirección, para muchos bucles complejos multi-direccionales de entrada de realimentación y capas. En general, estos sistemas utilizan algoritmos en su programación para determinar el control y la organización de sus funciones. La mayoría de los sistemas utilizan "pesos" para cambiar los parámetros del rendimiento y las diferentes conexiones con las neuronas. Las redes neuronales artificiales pueden ser autónomas y aprender mediante el aporte de "maestros" externos o incluso auto-enseñanza de las reglas escritas de entrada. Redes neuronales estilo Cubo Neural primera por primera vez por Gianna Giavelli proporcionan un espacio dinámico en el que las redes se recombinan dinámicamente información y enlaces a través de miles de millones de nodos independientes que utilizan la adaptación neuronal darwinismo , una técnica desarrollada por Gerald Edelman , que permite sistemas más modeladas biológicamente.
Potencia del cálculo
El perceptrón multicapa es un aproximado de la función universal, como lo demuestra el teorema de aproximación universal. Sin embargo, la prueba no es constructivo sobre el número de neuronas es necesario, la topología de red, la configuración de los pesos y los parámetros de aprendizaje.
El trabajo de Hava Siegelmann y Eduardo D. Sontag ha proporcionado una prueba de que una arquitectura específica recurrente con los pesos valorados racionales (en oposición a la precisión total número real -valued pesos) tiene toda la potencia de una máquina universal de Turing [59]utilizando un número finito de las neuronas y las conexiones lineales estándar. Además, se ha demostrado que el uso de valores irracionales para resultados pesos en una máquina con super-Turing poder.
Capacidad
Los modelos de redes neuronales artificiales tienen una propiedad denominada "capacidad", que corresponde aproximadamente a su capacidad para modelar cualquier función dada. Se relaciona con la cantidad de información que puede ser almacenada en la red y a la noción de complejidad.
Convergencia
Nada se puede decir en general sobre la convergencia ya que depende de una serie de factores. En primer lugar, pueden existir muchos mínimos locales. Esto depende de la función de coste y el modelo. En segundo lugar, el método de optimización utilizado no puede ser garantizado a converger cuando lejos de un mínimo local. En tercer lugar, para una cantidad muy grande de datos o parámetros, algunos métodos se vuelven poco práctico. En general, se ha encontrado que las garantías teóricas sobre la convergencia son una guía fiable para la aplicación práctica.
Generalización y estadísticas
En aplicaciones donde el objetivo es crear un sistema que generaliza bien en los ejemplos que no se ven, ha surgido el problema de la formación excesiva. Esto surge en los sistemas complicados o sobre especificadas cuando la capacidad de la red supera significativamente los parámetros libres necesarios. Hay dos escuelas de pensamiento para evitar este problema: La primera es utilizar la validación cruzada técnicas similares y para comprobar la presencia de un exceso de formación y de manera óptima seleccione hiper- tales que se minimice el error de generalización. La segunda es utilizar algún tipo de regularización . Este es un concepto que surge de manera natural en un marco probabilístico (Bayesiano), donde la regularización puede realizarse mediante la selección de una probabilidad a priori más grande sobre los modelos más simples; sino también en la teoría estadística de aprendizaje, donde el objetivo es reducir al mínimo más de dos cantidades: el "riesgo empírico" y el "riesgo estructural ', que corresponde aproximadamente al error sobre el conjunto de formación y el error de predicción en los datos que no se ven debido a sobreajuste. Redes neuronales supervisadas que utilicen un error cuadrático medio (MSE) función de coste se pueden utilizar métodos estadísticos formales para determinar la confianza del modelo formado. El MSE en un conjunto de validación se puede utilizar como una estimación de la varianza. Este valor puede ser utilizado para calcular el intervalo de confianza de la salida de la red, suponiendo una distribución normal . Un análisis de confianza realizado de esta manera es estadísticamente válida siempre que la salida de distribución de probabilidad sigue siendo el mismo y la red no es modificada.
Mediante la asignación de una función de activación softmax , una generalización de la función logística , en la capa de salida de la red neuronal (o un componente softmax en una red neuronal basada en componentes) para las variables categóricas de destino, las salidas se pueden interpretar como las probabilidades. Esto es muy útil en la clasificación, ya que da una medida de la seguridad en las clasificaciones.
La función de activación softmax es:
La crítica
Cosas de capacitación
Una crítica común de las redes neuronales, en particular en la robótica, es que requieren una gran diversidad de formación para el funcionamiento del mundo real. Esto no es sorprendente, ya que cualquier máquina de aprendizaje necesita suficientes ejemplos representativos con el fin de capturar la estructura subyacente que le permite generalizar a nuevos casos. Dean A. Powerless, en su investigación presentada en el documento "Formación basada en el conocimiento de redes neuronales artificiales para la conducción autónoma del robot", utiliza una red neuronal para formar a un vehículo robótico para conducir en múltiples tipos de carreteras (de un solo carril, varios carriles, suciedad, etc.). Una gran cantidad de su investigación está dedicada a (1) la extrapolación de múltiples escenarios de formación a partir de una sola experiencia de formación, y (2) la preservación de la diversidad de formación pasada para que el sistema no se convierta en sobre formación (si, por ejemplo, se presenta con una serie de giros a la derecha - no debe aprender a girar siempre a la derecha). Estos problemas son comunes en las redes neuronales que debe decidir de entre una amplia variedad de respuestas, pero se pueden tratar de varias maneras, por ejemplo por revolver al azar los ejemplos de formación, mediante el uso de un algoritmo de optimización numérica que no toma demasiado grandes pasos cuando el cambio de las conexiones de red siguiendo un ejemplo, o mediante la agrupación de ejemplos en los llamados mini-lotes.
Cuestiones teóricas
AK Dewdney , un científico matemático e informática de la Universidad de Ontario Occidental y ex columnista de Scientific American, escribió en 1997, "A pesar de que las redes neurales hacen resolver algunos problemas de juguete, su poder de computación son tan limitados que me sorprende que nadie los toma en serio como una herramienta general de resolución de problemas". No existe una red neuronal nunca se ha demostrado que resuelve los problemas computacionalmente difíciles, tales como la N-Queens problema, el problema del viajante de comercio, o el problema de factorizar enteros grandes.
Aparte de su utilidad, una objeción fundamental a las redes neuronales artificiales es que no logran reflejar cómo funcionan las neuronas reales. Propagación hacia atrás está en el corazón de las redes neuronales artificiales y la mayoría no sólo no hay evidencia de ningún mecanismo de este tipo de redes neuronales naturales,[54] parece contradecir el principio fundamental de las neuronas reales que la información sólo puede fluir hacia adelante a lo largo del axón. Como la información está codificada por las neuronas reales aún no se conoce. Lo que se sabe es que las neuronas sensoriales disparan potenciales de acción con mayor frecuencia con la activación del sensor y las células musculares tiran más fuertemente cuando sus neuronas motoras asociadas reciben los potenciales de acción con más frecuencia.[55] Aparte del caso más simple de solo transmisión de información de una neurona a un sensor de la neurona motora casi nada se conoce de los principios generales subyacentes de cómo se maneja la información por las redes neuronales reales.
El propósito de las redes neuronales artificiales no es necesariamente replicar la función neural real sino inspirarse en redes neuronales naturales como acercamiento a una computación, inherentemente paralela, que proporcione soluciones a problemas que hasta ahora han sido intratables. Por tanto, una afirmación central de las redes neuronales artificiales es que encarna algún principio general nuevo y potente para el procesamiento de la información. Por desgracia, estos principios generales están mal definidos y que a menudo se afirma que son emergentes de la red neuronal en sí. Esto permite la asociación estadística sencilla (la función básica de las redes neuronales artificiales), que se describe como el aprendizaje o el reconocimiento. Como resultado, las redes neuronales artificiales tienen, según Dewdney, un "algo para nada la calidad, que imparte un aura peculiar de la pereza y una clara falta de curiosidad acerca de lo bien que estos sistemas de computación son Ninguna mano humana (o la mente) interviene; soluciones. Se encuentran como por arte de magia, y nadie, al parecer, ha aprendido nada”.[56]
Los problemas de hardware
Para implementar software de redes neuronales grandes y eficaces deben emplearse considerables recursos de procesamiento y almacenamiento. Mientras que el cerebro ha adaptado su hardware a la tarea de procesamiento de señales a través de un Grafo de las neuronas, simular incluso una forma simplificada en la arquitectura von Neumann puede obligar a un diseñador de la red neural a utilizar muchos millones de filas de bases de datos para sus conexiones, lo que puede consumir grandes cantidades de espacio de memoria RAM y disco duro. Además, el diseñador de sistemas de redes neurales a menudo necesitará utilizar para simular la transmisión de señales a través de muchas de estas conexiones y sus neuronas asociadas una increíble cantidad de potencia de procesamiento y tiempo de CPU.
Jürgen Schmidhuber toma nota de que el resurgimiento de las redes neuronales en el siglo siglo XXI, y su éxito renovado en tareas de reconocimiento de imagen es atribuible en gran medida a los avances en el hardware: de 1991 a 2015, el poder de computación, especialmente en lo entregado por GPGPUs (en las GPU ), ha aumentado alrededor de un millón de veces, por lo que el algoritmo de retropropagación estándar viable para las redes de formación que son varias capas más profundas que antes (pero añade que esto no resuelve los problemas algorítmicos tales como el problema del desvanecimiento de gradientes "de una manera fundamental"). El uso de la GPU en lugar de CPUs ordinarios puede traer los tiempos de formación para algunas redes por debajo de los meses a meros días.
Potencia de cálculo sigue creciendo más o menos de acuerdo con la Ley de Moore , que puede proporcionar recursos suficientes para llevar a cabo nuevas tareas. Ingeniería neuromorphic aborda la dificultad de hardware directamente, mediante la construcción de chips de no-von Neumann con circuitos diseñados para implementar redes neuronales desde el principio. Google también ha diseñado un chip optimizado para el procesamiento de red neural llamado Unidad de Procesamiento Tensor o TPU.
Contraejemplos prácticas a las críticas
Argumentos en contra de la posición de Dewdney son que las redes neuronales se han utilizado con éxito para resolver muchas tareas complejas y diversas, que van desde aviones que vuelan de forma autónoma para la detección de fraude de tarjetas de crédito.
Escritor de tecnología Roger Bridgman ha comentado las declaraciones de DEWDNEY sobre redes neuronales:
Las redes neuronales, por ejemplo, están en el muelle no sólo porque han sido promocionado al alto cielo, (lo que tiene, no?), sino también porque se puede crear una red de éxito sin la comprensión de cómo funcionaba: el montón de números que captura su comportamiento sería con toda probabilidad "una, mesa ilegible opaca... sin valor como recurso científico".
A pesar de su enfática declaración de que la ciencia no es la tecnología, parece Dewdney aquí para ridiculizar a las redes neuronales como mala ciencia cuando la mayoría de los ideando ellos están tratando de ser buenos ingenieros. Una tabla puede leer que una máquina útil podía leer todavía sería bien vale la pena tener.
Si bien es cierto que el análisis de lo que se ha aprendido por una red neuronal artificial es difícil, es mucho más fácil de hacerlo que analizar lo que se ha aprendido por una red neuronal biológica. Por otra parte, los investigadores involucrados en la exploración de algoritmos de aprendizaje para redes neuronales están descubriendo gradualmente principios genéricos que permiten que una máquina de aprendizaje tenga éxito. Por ejemplo, Bengio y LeCun (2007) escribió un artículo sobre el aprendizaje locales vs. No locales, así como poco profundas frente a la arquitectura de profundidad.
Enfoques híbridos
Algunas otras críticas que provienen de los defensores de los modelos híbridos (combinación de redes neuronales y enfoques simbólicos), que creen que el intermix de estos dos enfoques puede capturar mejor los mecanismos de la mente humana.
Conclusión
Aunque en algunas facultades de informática se sigue instruyendo en redes neuronales artificiales, éstas no disponen de un rigor científico claro, y están consideradas como una pseudociencia por la mayoría de científicos e ingenieros.
Las clases y tipos de RNAs
- Red Neural dinámico
- Red neuronal feedforward (FNN)
- Red neuronal recurrente (RNN)
- Red de Hopfield
- Máquina de Boltzmann
- Redes recurrentes simples
- Red estatal de eco
- Memoria a largo plazo corto
- Bidireccional RNN
- Jerárquica RNN
- Redes neuronales estocásticas
- Mapas autoorganizados de Kohnen
- Autoencoder
- Red neuronal probabilística (PNN)
- Red neuronal de retardo de tiempo (TDNN)
- Red de realimentación reguladora (RFNN)
- Estática red neuronal
- Neocognitrón
- Neurona de McCulloch-Pitts
- Red de función de base radial (RBF)
- Aprender cuantificación vectorial
- perceptrón
- Modelo Adaline
- Red neuronal de convolución (CNN)
- redes neuronales modulares
- Comité de las máquinas (COM)
- Red neuronal asociativa (ASNN)
- Memoria Red
- Google / Google DeepMind
- Facebook / MemNN
- Memoria asociativa holográfica
- One-shot memoria asociativa
- Máquina de Turing neuronal
- Teoría de la resonancia adaptativa
- la memoria temporal jerárquica
- Otros tipos de redes
- Redes neuronales formadas instantáneamente (ITNN)
- Red neuronal de impulsos (SNN)
- Impulsión codificados Redes Neuronales (PCNN)
- En cascada redes neuronales
- Redes Neuro-Fuzzy
- Creciente de gas neural (GNG)
- Redes patrón productoras de composición
- Red de contrapropagación
- Red neuronal oscilante
- Red neural híbrida
- Red neuronal física
- Red neuronal óptica
- Red neuronal residual
Ejemplos
Quake II Neuralbot
Un bot es un programa que simula a un jugador humano. El Neuralbot es un bot para el juego Quake II que utiliza una red neuronal artificial para decidir su comportamiento y un algoritmo genético para el aprendizaje. Es muy fácil probarlo para ver su evolución. Más información aquí
Clasificador No Sesgado de Proteínas
Es un programa que combina diversas técnicas computacionales con el objetivo de clasificar familias de proteínas. Un posible método consiste en utilizar métricas adaptativas como por ejemplo: mapas autoorganizados y algoritmos genéticos.
El problema de clasificación no sesgada basada en la expresión de las proteínas en aminoácidos puede reducirse, conceptualmente, a lo siguiente:
- La identificación de grupos de proteínas que compartan características comunes.
- La determinación de las razones estructurales por las cuales las proteínas en cuestión se agrupan de la manera indicada.
- Evitar la idea de establecer criterios de clasificación (“sesgados”) fundamentados en ideas preconcebidas para lograr su clasificación. En este sentido, hay dos asuntos que considerar:
- Cómo lograr la caracterización de las proteínas de manera no sesgada
- Cómo lograr lo anterior sin apelar a medidas de agrupamiento que, a su vez, impliquen algún tipo de sesgo sobre dicho agrupamiento.
Las RNA han sido aplicadas a un número en aumento de problemas en la vida real y de considerable complejidad, donde su mayor ventaja es en la solución de problemas que son bastante complejos para la tecnología actual, tratándose de problemas que no tienen una solución algorítmica o cuya solución algorítmica es demasiado compleja para ser encontrada.
En general, debido a que son parecidas a las del cerebro humano, las RNA son bien nombradas ya que son buenas para resolver problemas que el humano puede resolver pero las computadoras no. Estos problemas incluyen el reconocimiento de patrones y la predicción del tiempo. De cualquier forma, el humano tiene capacidad para el reconocimiento de patrones, pero la capacidad de las redes neuronales no se ve afectada por la fatiga, condiciones de trabajo, estado emocional, y compensaciones.
Se conocen cinco aplicaciones tecnológicas extendidas:
- Reconocimiento de textos manuscritos
- Reconocimiento del habla
- Simulación de centrales de producción de energía
- Detección de explosivos
- Identificación de blancos de radares
Galería
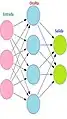
 Una sola capa de red neural artificial feedforward. Flechas procedentes de x2 se omiten para mayor claridad. Hay P entradas a esta red y salidas q. En este sistema, el valor de la salida q-ésima, y_qse calcula como y_q=K*(∑(x_i*w_iq )-b_q)
Una sola capa de red neural artificial feedforward. Flechas procedentes de x2 se omiten para mayor claridad. Hay P entradas a esta red y salidas q. En este sistema, el valor de la salida q-ésima, y_qse calcula como y_q=K*(∑(x_i*w_iq )-b_q)
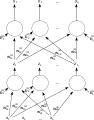 Una red neuronal artificial feedforward de dos capas.
Una red neuronal artificial feedforward de dos capas.
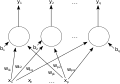
 Una red artificial de alimentación directa de una sola capa neuronal con 4 entradas, 6 ocultos y 2 salidas. Las salidas de estado y dirección determinada posición de la rueda basan los valores de control
Una red artificial de alimentación directa de una sola capa neuronal con 4 entradas, 6 ocultos y 2 salidas. Las salidas de estado y dirección determinada posición de la rueda basan los valores de control Una red artificial de alimentación directa de dos capas neuronales con 8 entradas, 2x8 ocultos y 2 salidas. Estado determinada posición, dirección y otro ambiente de valores. Los valores de control basados en salidas empujador.
Una red artificial de alimentación directa de dos capas neuronales con 8 entradas, 2x8 ocultos y 2 salidas. Estado determinada posición, dirección y otro ambiente de valores. Los valores de control basados en salidas empujador.
 Indefinido
Indefinido Indefinido
Indefinido
Herramientas de software
Existen muchas herramientas de software que implementan redes neuronales artificiales, tanto libres como comerciales como, por ejemplo:
Véase también
- Inteligencia artificial
- Dinámica de sistemas
- Sistema complejo
- Sistema dinámico
- Robótica evolutiva
- Conformación de haces (beamforming)
- Cerebro artificial
- Redes neuronales convolucionales
- Reservoir computing
- Perceptrón multicapa
- Deep Dream
- Ablación (inteligencia artificial)
- Confabulación (redes neuronales)
Referencias
- [url=http://www.itnuevolaredo.edu.mx/takeyas/apuntes/Inteligencia%20Artificial/Apuntes/tareas_alumnos/RNA/Redes%20Neuronales2.pdf «historia de las redes neurales»].
- McCulloch, Warren; Walter Pitts (1943). «A Logical Calculus of Ideas Immanent in Nervous Activity». Bulletin of Mathematical Biophysics 5 (4): 115-133. doi:10.1007/BF02478259.
- Figueroba, Alex. «Ley de Hebb: la base neuropsicológica del aprendizaje». Psicología y mente. Consultado el 24 de octubre de 2018.
- Hebb, Donald (1949). The Organization of Behavior [La Organización del Comportamiento]. Nueva York: Wiley. ISBN 978-1-135-63190-1.
- Republicación del artículode Turing de 1948: Turing, A.M. (1992). Collected works of AM Turing — Mechanical Intelligence. [Obras colectivas de AM Turing — Inteligencia mecánica] (en inglés). Elsevier Science Publishers.
- Webster, C.S. (2012). Alan Turing's unorganized machines and artificial neural networks: his remarkable early work and future possibilities [Las máquinas desorganizadas y redes de neuronas artificiales de Alan Turing: su notable trabajo inicial y posibilidades futuras] (en inglés publicación=Evolutionary Intelligence) (5). pp. 35-43. Webster CS. Alan Turing's unorganized machines and artificial neural networks: his remarkable early work and future possibilities. Evolutionary Intelligence 2012: 5; 35-43.
- Farley, B.G.; W.A. Clark (1954). «Simulation of Self-Organizing Systems by Digital Computer» [Simulación de Sistemas Autoorganizadoras por Computadora Digital]. IRE Transactions on Information Theory 4 (4): 76-84. doi:10.1109/TIT.1954.1057468.
- Rochester, N.; J.H. Holland; L.H. Habit; W.L. Duda (1956). «Tests on a cell assembly theory of the action of the brain, using a large digital computer» ["Pruebas de una teoría de la acción del cerebro por asamblea de células, usando una computadora digital grande]. IRE Transactions on Information Theory 2 (3): 80-93. doi:10.1109/TIT.1956.1056810.
- Matich, Damián Jorge (2001). «Redes Neuronales: Conceptos Básicos y Aplicaciones.» (PDF). Buenos Aires, Argentina. p. 6. Consultado el 26 de octubre de 2018.
- Rosenblatt, F. (1958). «The Perceptron: A Probabilistic Model For Information Storage And Organization In The Brain». Psychological Review 65 (6): 386-408. PMID 13602029. doi:10.1037/h0042519.
- Werbos, P.J. (1975). Beyond Regression: New Tools for Prediction and Analysis in the Behavioral Sciences. Harvard University.
- Hubel, David H.; Wiesel, Torsten (2005). Brain and visual perception: the story of a 25-year collaboration [Cerebro y percepción visual: la historia de una colaboración de 25 años]. Oxford University Press US. p. 106. ISBN 978-0-19-517618-6.
- Schmidhuber, J. (2015). «Deep Learning in Neural Networks: An Overview». Neural Networks 61: 85-117. PMID 25462637. arXiv:1404.7828. doi:10.1016/j.neunet.2014.09.003.
- Ivakhnenko, A. G. (1973). Cybernetic Predicting Devices. CCM Information Corporation.
- Ivakhnenko, A. G.; Grigorʹevich Lapa, Valentín (1967). Cybernetics and forecasting techniques. American Elsevier Pub. Co.
- Minsky, Marvin; Papert, Seymour (1969). Perceptrons: An Introduction to Computational Geometry. MIT Press. ISBN 0-262-63022-2.
- Rumelhart, D.E; McClelland, James (1986). Parallel Distributed Processing: Explorations in the Microstructure of Cognition. Cambridge: MIT Press. ISBN 978-0-262-63110-5.
- Qian, N.; Sejnowski, T.J. (1988). «Predicting the secondary structure of globular proteins using neural network models.». Journal of Molecular Biology 202: 865-884. Qian1988.
- Rost, B.; Sander, C. (1993). «Prediction of protein secondary structure at better than 70% accuracy». Journal of Molecular Biology 232: 584-599. Rost1993.
- Weng, J.; Ahuja, N.; Huang, T. S. (1992). «Cresceptron: a self-organizing neural network which grows adaptively». Proc. International Joint Conference on Neural Networks (Baltimore, Maryland) 1: 576-581.
- Weng, J.; Ahuja, N.; Huang, T.S. (1993). «Learning recognition and segmentation of 3-D objects from 2-D images». Proc. 4th International Conf. Computer Vision (Berlin, Alemania): 121-128.
- Weng, J.; Ahuja, N.; Huang, T.S. (1997). «Learning recognition and segmentation using the Cresceptron». International Journal of Computer Vision 25 (2): 105-139.
- Scherer, Dominik; Müller, Andreas C.; Behnke, Sven (2010). «Evaluation of Pooling Operations in Convolutional Architectures for Object Recognition». 20th International Conference Artificial Neural Networks (ICANN): 92-101. doi:10.1007/978-3-642-15825-4_10.
- S. Hochreiter., "Untersuchungen zu dynamischen neuronalen Netzen," Diploma thesis. Institut f. Informatik, Technische Univ. Munich. Advisor: J. Schmidhuber, 1991.
- Hochreiter, S.; et al. (15 de enero de 2001). «Gradient flow in recurrent nets: the difficulty of learning long-term dependencies». En Kolen, John F.; Kremer, Stefan C., eds. A Field Guide to Dynamical Recurrent Networks. John Wiley & Sons. ISBN 978-0-7803-5369-5.
- J. Schmidhuber., "Learning complex, extended sequences using the principle of history compression," Neural Computation, 4, pp. 234–242, 1992.
- Behnke, Sven (2003). Hierarchical Neural Networks for Image Interpretation.. Lecture Notes in Computer Science 2766. Springer.
- Yang, J. J.; Pickett, M. D.; Li, X. M.; Ohlberg, D. A. A.; Stewart, D. R.; Williams, R. S. (2008). «Memristive switching mechanism for metal/oxide/metal nanodevice». Nat. Nanotechnol. 3: 429-433. doi:10.1038/nnano.2008.160.
- Strukov, D. B.; Snider, G. S.; Stewart, D. R.; Williams, R. S. (2008). «The missing memristor found». Nature 453 (7191): 80-83. Bibcode:2008Natur.453...80S. PMID 18451858. doi:10.1038/nature06932.
- Cireşan, Dan Claudiu; Meier, Ueli; Gambardella, Luca María; Schmidhuber, Jürgen (21 de septiembre de 2010). «Deep, Big, Simple Neural Nets for Handwritten Digit Recognition». Neural Computation 22 (12): 3207-3220. ISSN 0899-7667. doi:10.1162/neco_a_00052.
- Yang, J. J.; Pickett, M. D.; Li, X. M.; Ohlberg, D. A. A.; Stewart, D. R.; Williams, R. S. (2008). «Memristive switching mechanism for metal/oxide/metal nanodevices». Nat. Nanotechnol. 3 (7): 429-433. doi:10.1038/nnano.2008.160.
- Strukov, D. B.; Snider, G. S.; Stewart, D. R.; Williams, R. S. (2008). «The missing memristor found». Nature 453 (7191): 80-83. Bibcode:2008Natur.453...80S. PMID 18451858. doi:10.1038/nature06932.
- Cireşan, Dan; Meier, Ueli; Masci, Jonathan; Schmidhuber, Jürgen (Agosto de 2012). «Multi-column deep neural network for traffic sign classification». Neural Networks. Selected Papers from IJCNN 2011 32: 333-338. doi:10.1016/j.neunet.2012.02.023.
- Ciresan, Dan; Giusti, Alessandro; Gambardella, Luca M.; Schmidhuber, Juergen (2012). Pereira, F.; Burges, C. J. C.; Bottou, L. et al., eds. Advances in Neural Information Processing Systems 25. Curran Associates, Inc. pp. 2843-2851.
- «The Machine Learning Dictionary». Archivado desde el original el 26 de agosto de 2018. Consultado el 19 de septiembre de 2018.
- Ojha, Varun Kumar; Abraham, Ajith; Snášel, Václav (1 de abril de 2017). «Metaheuristic design of feedforward neural networks: A review of two decades of research». Engineering Applications of Artificial Intelligence 60: 97-116. doi:10.1016/j.engappai.2017.01.013.
- Dominic, S.; Das, R.; Whitley, D.; Anderson, C. (July 1991). «Genetic reinforcement learning for neural networks». IJCNN-91-Seattle International Joint Conference on Neural Networks (Seattle, Washington, USA: IEEE). ISBN 0-7803-0164-1. doi:10.1109/IJCNN.1991.155315.
- Hoskins, J.C.; Himmelblau, D.M. (1992). «Process control via artificial neural networks and reinforcement learning». Computers & Chemical Engineering 16 (4): 241-251. doi:10.1016/0098-1354(92)80045-B.
- Bertsekas, D.P.; Tsitsiklis, J.N. (1996). Neuro-dynamic programming. Athena Scientific. p. 512. ISBN 1-886529-10-8.
- de Rigo, D.; Rizzoli, A. E.; Soncini-Sessa, R.; Weber, E.; Zenesi, P. (2001). «Neuro-dynamic programming for the efficient management of reservoir networks». Proceedings of MODSIM 2001, International Congress on Modelling and Simulation (Canberra, Australia: Modelling and Simulation Society of Australia and New Zealand). ISBN 0-867405252. doi:10.5281/zenodo.7481. Consultado el 29 de julio de 2012.
- Damas, M.; Salmeron, M.; Díaz, A.; Ortega, J.; Prieto, A.; Olivares, G. (2000). «Genetic algorithms and neuro-dynamic programming: application to water supply networks». Proceedings of 2000 Congress on Evolutionary Computation (La Jolla, California, USA: IEEE). ISBN 0-7803-6375-2. doi:10.1109/CEC.2000.870269.
- Deng, Geng; Ferris, M.C. (2008). «Neuro-dynamic programming for fractionated radiotherapy planning». Springer Optimization and Its Applications. Springer Optimization and Its Applications 12: 47-70. ISBN 978-0-387-73298-5. doi:10.1007/978-0-387-73299-2_3.
- M. Forouzanfar; H. R. Dajani; V. Z. Groza; M. Bolic; S. Rajan (July 2010). Comparison of Feed-Forward Neural Network Training Algorithms for Oscillometric Blood Pressure Estimation. Arad, Romania: IEEE.
- de Rigo, D.; Castelletti, A.; Rizzoli, A. E.; Soncini-Sessa, R.; Weber, E. (January 2005). «A selective improvement technique for fastening Neuro-Dynamic Programming in Water Resources Network Management». En Pavel Zítek, ed. Proceedings of the 16th IFAC World Congress – IFAC-PapersOnLine (Prague, Czech Republic: IFAC) 16. ISBN 978-3-902661-75-3. doi:10.3182/20050703-6-CZ-1902.02172. Consultado el 30 de diciembre de 2011.
- Ferreira, C. (2006). «Designing Neural Networks Using Gene Expression Programming». In A. Abraham, B. de Baets, M. Köppen, and B. Nickolay, eds., Applied Soft Computing Technologies: The Challenge of Complexity, pages 517–536, Springer-Verlag.
- Da, Y.; Xiurun, G. (July 2005). «An improved PSO-based ANN with simulated annealing technique». En T. Villmann, ed. New Aspects in Neurocomputing: 11th European Symposium on Artificial Neural Networks (Elsevier). doi:10.1016/j.neucom.2004.07.002.
- Wu, J.; Chen, E. (May 2009). Wang, H., Shen, Y., Huang, T., Zeng, Z., ed. A Novel Nonparametric Regression Ensemble for Rainfall Forecasting Using Particle Swarm Optimization Technique Coupled with Artificial Neural Network. Springer. ISBN 978-3-642-01215-0. doi:10.1007/978-3-642-01513-7-6.
- Ting Qin, et al. "A learning algorithm of CMAC based on RLS." Neural Processing Letters 19.1 (2004): 49–61.
- Ting Qin, et al. "Continuous CMAC-QRLS and its systolic array." Neural Processing Letters 22.1 (2005): 1–16.
- Zissis, Dimitrios (October 2015). «A cloud based architecture capable of perceiving and predicting multiple vessel behaviour». Applied Soft Computing 35: 652-661. doi:10.1016/j.asoc.2015.07.002.
- Sengupta, Nandini; Sahidullah, Md; Saha, Goutam (August 2016). «Lung sound classification using cepstral-based statistical features». Computers in Biology and Medicine 75 (1): 118-129. doi:10.1016/j.compbiomed.2016.05.013.
- Schechner, Sam (15 de junio de 2017). «Facebook Boosts A.I. to Block Terrorist Propaganda». Wall Street Journal (en inglés estadounidense). ISSN 0099-9660. Consultado el 16 de junio de 2017.
- https://nmas1.org/news/2018/06/22/fb-musica-ra-tecnologia
- Crick, Francis (1989). «The recent excitement about neural networks». Nature 337 (6203): 129-132. Bibcode:1989Natur.337..129C. PMID 2911347. doi:10.1038/337129a0.
- Adrian, Edward D. (1926). «The impulses produced by sensory nerve endings». The Journal of Physiology 61 (1): 49-72. PMC 1514809. PMID 16993776. doi:10.1113/jphysiol.1926.sp002273.
- Dewdney, A. K. (1 de abril de 1997). Yes, we have no neutrons: an eye-opening tour through the twists and turns of bad science. Wiley. p. 82. ISBN 978-0-471-10806-1.
Enlaces externos
 Wikimedia Commons alberga una galería multimedia sobre Red neuronal artificial.
Wikimedia Commons alberga una galería multimedia sobre Red neuronal artificial.- Tutorial de la Universidad Politécnica de Madrid (español)
- Introducción a las redes de neuronas artificiales (español)
- Artículos sobre redes neuronales artificiales (inglés)
- Sitio web sobre redes neuronales artificiales, ejemplos y aplicaciones (español)
- Introducción a las Redes Neuronales y sus Modelos (español)
- Sistema nervioso artificial
- ¿Qué son las redes neuronales?(español)
- neural-network repositorio en GitHub (PHP)
- Entiende como funcionan las redes neuronales en menos de 10 minutos (español)