Signo de integración
El símbolo ∫ se usa para denotar una integral en matemáticas. La notación fue introducida por el matemático y filósofo alemán Gottfried Leibniz (1646-1716) a finales del siglo XVII, en sus cuadernos el 21 de noviembre de 1675, aunque oficialmente aparece en una primera impresión publica en el Acta Eruditium llamada el El Calculus en 1684, este informe se desestimó porque presentaba algunos errores, sin embargo, estuvo presente el nacimiento del símbolo de la integral, como proceso de antiderivación. El símbolo se basó en el carácter ſ (S larga), y se escogió debido a que una integral es el límite de una suma de partes de áreas entre una función y el eje de las abscisas.
El Símbolo ∫ es U+222B en Unicode, \int en LaTeX. En HTML, se escribe ∫ en (hexadecimal), ∫ (decimal) y ∫.
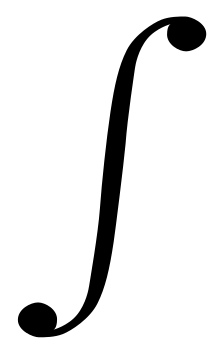
El paquete de caracteres de la página de código 437 de IBM PC original tenía un par de caracteres ⌠ y ⌡ (códigos 244 y 245, respectivamente) para construir el símbolo. Estos fueron remplazados en las subsecuentes páginas de código de MS-DOS, pero siguen existiendo en Unicode (U+2320 y U+2321, respectivamente) por compatibilidad.
El símbolo ∫ es bastante similar, pero no debe confundirse con símbolo (ʃ) llamado esh.
Símbolos relacionados son ∬ (integral doble, U+222C), ∭ (integral triple, U+222D), ∮ (integral de contorno, U+222E), ∯ (integral de superficie, U+222F), y ∰ (integral de volumen, U+2230).
Referencias
- Stewart, James (2003). «Integrals». Single Variable Calculus: Early Transcendentals (5.ª edición). Belmont, CA: Brooks/Cole. pp. 381. ISBN 0-534-39330-6. Consultado el 26 de junio de 2006.
- Bernoulli, Johann (1924). «Differential Calculus». Die Differential rechnung aus dem Jahre 1691/1692 (Vol 1 edición). Universidad Lepzig, Alemania, Otswald's klassiker der exakten Wissenschaften; N211: Akademische verlagsgesellschaft. p. 56. ISSN 0232-3419.