Équation de Pell-Fermat

L'histoire de l'équation de Pell-Fermat est particulièrement riche et ancienne. On[3] cite parfois le problème des bœufs d'Hélios attribué à Archimède[4] comme premier exemple d'équation de Pell-Fermat. Il n'est cependant pas certain qu'Archimède en soit l'auteur et que la relation avec ladite équation ait été faite. En revanche, Diophante d'Alexandrie, un mathématicien vivant probablement au III^e siècle parle explicitement d'une équation de cette nature, dans son livre intitulé Arithmetica. Avec les notations du paragraphe Définitions, il étudie le cas où n est égal à 1 et m à 1, –1 ou 12 ainsi que le cas où n et m sont égaux à 9[5]. Dès avant notre ère, les Grecs connaissaient l'existence de l'égalité suivante[6] :

${\displaystyle 577^{2}-2\cdot 408^{2}=1.}$

Le mathématicien indien Brahmagupta (598-668) semble être le premier à travailler profondément sur la question, il étudie le cas où m = 1. En 628, il établit une égalité permettant, à l'aide de deux solutions de l'équation, d'en construire une troisième[7]. Ainsi, en combinant deux fois la même solution, il en obtient une nouvelle et ainsi de suite, ce qui donne un nombre de solutions aussi grand que désiré. Cette méthode lui permet d'aller plus loin. À l'aide d'un couple (x, y) d'entiers tel que x² –ny² soit égal à ±2, Brahmagupta construit une solution. Puis à l'aide d'un algorithme guère plus complexe, il obtient un résultat analogue si x² – ny² est égal à ±4. Par tâtonnements, il parvient à trouver des solutions dans de nombreuses configurations. Son outil principal est l'algorithme d'Euclide, généralement nommé par les Indiens le pulvérisateur car il casse les nombres en morceaux de plus en plus petits[8].

L'étape suivante est franchie par Bhāskara II, un mathématicien indien du XII^e siècle. Il enrichit la palette de techniques de Brahmagupta, et présente une méthode complète, nommée chakravala. Elle correspond à un algorithme astucieux permettant de déterminer une solution primitive, c'est-à-dire une solution qui génère toutes les autres[9]. Il n'est pas dans l'usage des mathématiciens indiens de cette époque de rechercher une preuve autre qu'expérimentale. Quant à l'exhaustivité de l'ensemble des solutions trouvées, la question n'est pas non plus abordée.

Joseph-Louis Lagrange démontre l'existence d'une infinité de solutions si m = ±1 et montre que l'algorithme des fractions continues permet de les obtenir toutes.

La popularité de cette équation provient d'un défi que Pierre de Fermat lance à Bernard Frénicle de Bessy en février 1657 (à la suite d'un autre défi plus célèbre datant du 3 janvier de la même année) ; il lui pose plusieurs questions dont celle d'une solution à l'équation de Pell-Fermat, déjà trouvée par Brahmagupta et Bhāskara II, elle correspond au cas n = 61 et m = 1 (il propose également le cas n = 109)[10]. Une communication épistolaire s'ensuit, finalement publiée par John Wallis[11], entre Kenelm Digby, William Brouncker et Wallis pour l'Angleterre, Frans van Schooten pour la Belgique et Bernard Frénicle de Bessy pour la France[12]. Elle nous indique que Brouncker découvre une méthode équivalente à celle des Indiens, sans néanmoins apporter plus de preuves que ses prédécesseurs. Frénicle de Bessy calcule l'intégralité des solutions pour n inférieur ou égal à 150, mais ses travaux sont perdus. Il défie Brouncker avec une valeur de 313 pour n. Brouncker propose une solution primitive, et précise qu'il ne lui a pas fallu plus « d'une heure ou deux » pour trouver. La réponse est la suivante :

${\displaystyle x=32\,188\,120\,829\,134\,849\quad {\text{et}}\quad y=1\,819\,380\,158\,564\,160.}$

Wallis démontre rigoureusement les résultats de Brahmagupta, c'est-à-dire la raison qui permet de trouver une solution si la valeur atteinte est 2 ou 4 en valeur absolue. En 1658, Johann Heinrich Rahn publie un livre d'algèbre, contenant un exemple d'équation maintenant dite de Pell-Fermat[13], relu et traduit en anglais par John Pell (1611-1685). C'est la seule contribution connue du mathématicien sur l'équation portant maintenant son nom.

Plusieurs mathématiciens affirment qu'il existe une solution pour toute valeur de n (à condition de choisir m égal à 1)[14], Fermat affirme de plus que le nombre de solutions est infini. En revanche aucune preuve de cette époque n'est connue.

Leonhard Euler (1707-1783) reprend les travaux de Brouncker et ceux de Wallis, proposant le formalisme de la fraction continue, équivalent à l'algorithme développé par Bhāskara II^{[Information douteuse]}. Seule la fin est différente ; une fois trouvée une valeur égale à ±2 ou ±4 en valeur absolue, il est en effet plus rapide d'utiliser le lemme de Brahmagupta. Euler attribue à tort les travaux passés à Pell[6]. Joseph-Louis Lagrange (1736-1813) reprend les travaux d'Euler et ajoute les deux preuves manquantes. Il démontre que pour toute valeur de n il existe une infinité de solutions et que toutes ces solutions sont générées par celle issue de l'algorithme des fractions continues[15]. Durant toute cette époque, l'Europe est inconsciente des travaux de leurs prédécesseurs indiens.

Richard Dedekind formalise le concept d'anneau portant maintenant son nom et élucide les propriétés permettant de résoudre l'équation de Pell-Fermat.

La méthode chakravala ou celle des fractions continues ont apporté tout ce qu'elles pouvaient sur cette équation, ce qui revient à traiter le cas du paramètre m égal à ±1. Le cas général demande de nouvelles idées et un siècle est encore nécessaire pour en venir à bout. Une approche fondatrice est l'œuvre de Carl Friedrich Gauss (1777-1855). Il travaille[16] sur des structures munies d'une addition et d'une multiplication, mais qui ne sont pas celles de l'anneau des entiers. Une de ces structures est celle des entiers de Gauss, c'est-à-dire des nombres de la forme a + ib où a et b sont des entiers et i l'unité imaginaire des nombres complexes. Un tel monde possède une division euclidienne, ce qui permet d'établir le théorème de Bachet-Bézout, le lemme d'Euclide ainsi que le théorème fondamental de l'arithmétique. Un tel anneau possède des nombres premiers de Gauss, et une approche similaire à celle de l'arithmétique dans Z est possible. Cette approche est maintenant le cadre d'une théorie appelée arithmétique modulaire. Une démarche de cette nature permet de venir à bout d'une équation diophantienne semblable à celle de Pell-Fermat, traité par le théorème des deux carrés de Fermat. Si i est remplacé, par exemple par le nombre d'or, égal à (1 + √5)/2, on obtient une structure un peu similaire, aussi euclidienne, correspondant à l'équation de Pell-Fermat pour le paramètre n égal à 5, et il est possible d'y traiter l'équation pour toute valeur du paramètre n, à condition de disposer de la loi de réciprocité quadratique, démontrée par Gauss. Cette loi correspond encore à une équation diophantienne un peu similaire.

Les travaux de Gauss apportent deux progrès : ils offrent un bon cadre pour étudier l'équation de Pell-Fermat et ils permettent de la résoudre intégralement dans le cas où ce cadre est euclidien. Il existe cependant de nombreux cas où le caractère euclidien est absent. Ce cadre, euclidien ou non, porte le nom d'anneau d'entiers algébriques et pour la résolution de l'équation de Pell-Fermat, une petite partie est utile, ceux formés par des entiers quadratiques. Johann Peter Gustav Lejeune Dirichlet (1805-1859) étudie et explicite leur groupe des unités dans le cas général. Ce groupe correspond exactement aux solutions de l'équation de Pell-Fermat pour m = ±1, fournissant une preuve différente de celle de Lagrange, et qui se généralise à tous les anneaux d'entiers algébriques et non pas uniquement quadratiques[17]. Si ce résultat fait progresser la théorie des nombres, il ne permet pas de débloquer la question de l'équation de Pell-Fermat dans le cas général, car il ne concerne que les solutions pour le paramètre m égal à ±1.

Si les techniques de Gauss fonctionnent, c'est grâce à l'équivalent des nombres premiers et au théorème fondamental de l'arithmétique, que l'on trouve dans tout anneau euclidien. Des anneaux disposant de propriétés ou d'axiomes plus faibles ont un équivalent, on les appelle les anneaux factoriels. Dans le cas général, un anneau d'entiers algébriques n'est ni euclidien ni factoriel. Richard Dedekind (1831-1916), à la suite des travaux de Ernst Kummer (1810-1893), trouve la bonne approche. Il met en évidence les axiomes que vérifient les bons anneaux d'entiers algébriques, lesquels portent maintenant le nom d'anneaux de Dedekind. À l'aide de cette nouvelle structure, il établit un équivalent du théorème fondamental de l'arithmétique[18]. Un deuxième théorème, traitant du groupe des classes d'idéaux permet de trouver toutes les solutions de l'équation de Pell-Fermat et pour toutes valeurs de n[19].

Dans son ouvrage Amusements in Mathematics paru en 1917, Henry Dudeney pose l'énigme de la bataille d'Hastings : combien étaient les hommes de Harold, groupés en 61 carrés identiques et n'en formant plus qu'un seul lorsque leur chef les a rejoints[20] ?

La réponse à cette énigme est tout à fait irréaliste (3 119 882 982 860 264 400 hommes).

Il est possible que cette énigme ait paru dans un magazine plusieurs années avant la publication du recueil puisque Martin Gardner signale que Sam Loyd, mort en 1911, l'a modifiée (13 carrés au lieu de 61) afin de rendre la réponse plus réaliste (421 200 hommes)[21].

Cette méthode part initialement d'une utilisation judicieuse de la formule suivante, nommée identité de Brahmagupta :

${\displaystyle \forall a_{1},b_{1},a_{2},b_{2}\in \mathbb {Z} \quad (a_{1}^{2}-nb_{1}^{2})(a_{2}^{2}-nb_{2}^{2})=(a_{1}a_{2}+nb_{1}b_{2})^{2}-n(a_{1}b_{2}+b_{1}a_{2})^{2}.}$

Ainsi, si (a₁, b₁) et (a₂, b₂) forment deux couples de solutions, l'identité précédente montre que (a₁a₂ + nb₁b₂, a₁b₂ + b₁a₂) est encore une solution. Il est judicieux d'équiper l'ensemble Z² des couples d'entiers d'une loi de composition interne * :

${\displaystyle \forall (a_{1},b_{1})(a_{2},b_{2})\in \mathbb {Z} ^{2}\quad (a_{1},b_{1})*(a_{2},b_{2})=(a_{1}a_{2}+nb_{1}b_{2},a_{1}b_{2}+b_{1}a_{2}).}$

L'ensemble Z² muni de cette loi interne est un monoïde commutatif, c'est-à-dire que la loi est associative et possède un élément neutre — le couple (1, 0) — et qu'elle est commutative. D'après l'identité de Brahmagupta, le sous-ensemble G des solutions de l'équation pour m = ±1 est stable pour la loi * et chaque élément (a, b) de G possède un symétrique dans G : le couple (a, –b) ou (–a, b), selon que a² – nb² est égal à 1 ou à –1. Ainsi, (G, *) forme un groupe abélien.

L'étude de ce groupe permet la mise au point d'une méthode efficace de résolution pour les valeurs de m égales à ±1. Par exemple, si α est un élément de G, solution pour la valeur m = –1, α² est une solution pour la valeur m = 1. Celle du monoïde (Z², *) permet de relier ces solutions à celles pour d'autres valeurs de m. Par exemple si α est solution pour la valeur m = ± 2 alors α²/2 est une solution pour la valeur m = 1. Enfin, si α est solution pour la valeur m = ± 4 alors α³/8 est — moyennant certaines hypothèses pour que ses deux composantes soient entières — une solution pour la valeur m = ± 1.

L'article détaillé propose une méthode exhaustive permettant de trouver une solution dans tous les cas, à partir des propriétés de la multiplication *. Il montre aussi comment cette méthode permet d'élucider la structure du groupe des solutions.

Une manière commode de voir ce groupe est d'identifier le couple (a, b) avec le nombre réel a + √nb. Cet ensemble forme un anneau, noté Z[√n]. Le groupe G s'identifie au groupe des unités de Z[√n], c'est-à-dire au groupe des éléments inversibles de l'anneau. Pour cette raison, une solution de l'équation s'écrit souvent a + √nb. Une identité remarquable montre la relation :

${\displaystyle a^{2}-nb^{2}=(a+b{\sqrt {n}})(a-b{\sqrt {n}}).}$

Les solutions de l'équation de Pell-Fermat pour m = ±1 se trouvent toutes sur une des branches des deux hyperboles.

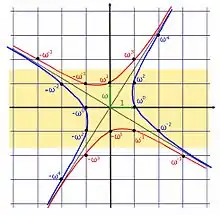
Résoudre l'équation x² – ny² = ±1 revient finalement à expliciter les éléments du groupe des unités de l'anneau Z[√n]. Ce groupe G est isomorphe au produit direct du groupe cyclique à deux éléments Z/2Z et de Z. Il existe toujours un élément α du groupe qui engendre toutes les autres, ce qui justifie la définition d'unité fondamentale, c'est-à-dire un élément α de G tel que :

${\displaystyle \forall \beta \in G\quad \exists e\in \{0,1\},\;\exists k\in \mathbb {Z} \quad {\text{tels que}}\quad \beta =(-1)^{e}\alpha ^{k}.}$

L'existence d'une unité fondamentale pour toute valeur de n positif et non carré est démontrée dans l'article détaillé. On parle parfois aussi de racine primitive.

Soient α une unité fondamentale et a et b les deux entiers tels que : α = a + √nb. Le groupe G contient exactement quatre unités fondamentales : a + √nb, a – √nb, –a + √nb et –a – √nb.

Cette propriété est une conséquence directe du théorème de structure énoncé en début de paragraphe. La figure de droite illustre le cas où n est égal à 5. L'anneau Z[√5] est un sous-anneau de l'anneau des entiers de Q(√5). Les différents éléments de G se trouvent sur quatre branches d'hyperboles. Il existe deux droites asymptotes, d'équation x = ± √ny.

Une solution de l'équation de Pell-Fermat est une bonne approximation fractionnaire de la racine carrée. Dans le cas général, une fraction de type p/q approxime un irrationnel avec une précision de 1/q ou 1/(2q)^[pas clair]. Une solution de l'équation de Pell-Fermat est plus précise. En effet, si (a, b) est une solution :

${\displaystyle \left|a^{2}-nb^{2}\right|=1\quad {\text{et}}\quad \left|{\frac {a}{b}}-{\sqrt {n}}\right|\left|{\frac {a}{b}}+{\sqrt {n}}\right|={\frac {1}{b^{2}}}.}$

Comme √n > 1 et a/b ≥ 1, on obtient l'approximation suivante :

${\displaystyle \left|{\frac {a}{b}}-{\sqrt {n}}\right|<{\frac {1}{2b^{2}}}}$.

On en déduit que a et b sont le numérateur et le dénominateur d'une réduite de la fraction continue de √n, c'est-à-dire que (pour un certain entier k) :

${\displaystyle {\frac {a}{b}}=[f_{0},f_{1},f_{2},\dots ,f_{k}],\quad {\text{avec}}\quad {\sqrt {n}}=[f_{0},f_{1},f_{2},\dots ,f_{k},\dots ].}$

Le développement en fraction continue de la racine carrée d’un entier non carré est périodique à partir du rang 1, c'est-à-dire qu'il est de la forme

${\displaystyle {\sqrt {n}}=[f_{0},f_{1},f_{2},\cdots ,f_{p-1},f_{p},f_{1},f_{2},\cdots ,f_{p-1},f_{p},f_{1},\cdots ]=[f_{0},{\overline {f_{1},f_{2},\cdots ,f_{p}}}]}$.

La première réduite solution de l'équation de Pell est celle d'indice p – 1. Par exemple, si n est égal à 29, on trouve f₀ = 5, ce qui correspond à la partie entière de la racine carrée, puis la période (2, 1, 1, 2, 10). La solution correspond à la fraction continue

${\displaystyle [5,2,1,1,2]={\frac {70}{13}}\quad {\rm {et}}\quad 70^{2}-29\cdot 13^{2}=4900-4901=-1}$.

Cette approche permet de démontrer simplement l'existence d'une unité fondamentale.

Si (a, b) satisfait une équation de Pell du type x² – ny² = ±1, alors a + √nb est un élément du groupe des unités de l'anneau des entiers de l'extension quadratique Q(√n), puisque (a + √nb)(a – √nb) = ±1. Le groupe des unités ainsi que l'équation de Pell est étudié dans le cas n = 5 dans l'article « Anneau des entiers de Q(√5) ». Cette analyse montre la relation entre les équations de Pell et la théorie algébrique des nombres.

Si ${\displaystyle {\sqrt {n}}=[a_{0},{\overline {a_{1},a_{2},a_{3},\ldots ,a_{p-1},a_{p}}}]}$, alors l'équation de Pell x² – ny² = 1 admet, suivant la parité de p, la solution « minimale » ${\displaystyle (x_{1},y_{1})}$ suivante :

• quand p est pair, le couple ${\displaystyle (x_{1},y_{1})=(h_{p-1},k_{p-1})}$ où ${\displaystyle {\frac {h_{p-1}}{k_{p-1}}}}$ est la réduite de rang p – 1 de √n
• quand p est impair, le couple ${\displaystyle (x_{1},y_{1})=(h_{2p-1},k_{2p-1})\,}$ où ${\displaystyle {\frac {h_{2p-1}}{k_{2p-1}}}}$ est la réduite de rang 2p – 1 de √n

La réduite de rang r de √n étant la fraction irréductible ${\displaystyle {\frac {h_{r}}{k_{r}}}=[a_{0},a_{1},\ldots ,a_{r}].}$

Les autres solutions ${\displaystyle (x_{k},y_{k})}$ avec k ≥ 1 sont obtenues en identifiant ${\displaystyle x_{k}+y_{k}{\sqrt {n}}}$ au développement de ${\displaystyle (x_{1}+y_{1}{\sqrt {n}})^{k}.}$

En particulier, ${\displaystyle (x_{2},y_{2})=(x_{1}^{2}+ny_{1}^{2},\ 2x_{1}y_{1})\,}$, ${\displaystyle (x_{3},y_{3})=(x_{1}^{3}+3nx_{1}y_{1}^{2},\ 3x_{1}^{2}y_{1}+ny_{1}^{3})\,}$, etc.

La formule de récurrence étant : ${\displaystyle (x_{k+1},y_{k+1})=(x_{k}x_{1}+ny_{k}y_{1},\ x_{k}y_{1}+y_{k}x_{1}).}$

Il existe des solutions si et seulement si l'unité fondamentale α = a + √nb en fournit une, c'est-à-dire si a² – nb² = –1, et les autres sont alors les couples fournis par les puissances impaires de α — les ${\displaystyle (x_{k},y_{k})}$ vérifiant ${\displaystyle x_{k}+y_{k}{\sqrt {n}}=(a+b{\sqrt {n}})^{k}}$ avec k entier relatif impair — et leurs opposés.

Exemple : n = 2, 5

L'unité fondamentale de Z[√2] est ±1 ± √2. Le couple (1, 1) est solution de x² – 2y² = –1. Les développements${\displaystyle (1+{\sqrt {2}})^{3}=7+5{\sqrt {2}},\quad (1+{\sqrt {2}})^{5}=41+29{\sqrt {2}},\quad (1+{\sqrt {2}})^{7}=239+169{\sqrt {2}}}$fournissent les solutions (7, 5), (41, 29) et (239, 169).

L'unité fondamentale de Z[√5] est ±2 ± √5. Le couple (2, 1) est solution de x² – 5y² = –1. Les développements${\displaystyle (2+{\sqrt {5}})^{3}=38+17{\sqrt {5}},\quad (2+{\sqrt {5}})^{5}=682+305{\sqrt {5}},\quad (2+{\sqrt {5}})^{7}=12\,238+5\,473{\sqrt {5}}}$fournissent les solutions (38, 17), (682, 305) et (12 238, 5 473).

Si n est congru à 1 mod 4, l'anneau des entiers de Q(√n) est égal à ℤ[(1 + √n)/2] donc contient strictement ℤ[√n]. Mais même en élargissant à ce domaine la recherche d'éléments de norme –1, il n'en existe que si le développement de √n en fraction continue est de période impaire (ce qui n'est pas le cas, par exemple, pour √21 = [4, 1, 1, 2, 1, 1, 8] : l'unité fondamentale (5 + √21)/2 de ℤ[(1 + √21)/2] est de norme +1).

 : document utilisé comme source pour la rédaction de cet article.

• Serge Coquerand: L’équation de Pell-Fermat x2−dy2=1 revisitée - Le problème des bœufs d’Hélios. Publibook, 2015.
• (en) David A. Cox, Primes of the Form x² + ny², John Wiley & Sons, 2011 (1^re éd. 1989) (ISBN 978-1-11803100-1, lire en ligne)
• Roger Descombes, Éléments de théorie des nombres, PUF, 1986
• (en) Alexandre Junod, « An algorithm to solve a Pell equation », General Mathematics Notes, vol. 28, n^o 2,‎ 2015, p. 1-8 (lire en ligne)
• (en) Hendrik Lenstra, « Solving the Pell Equation », Notices Amer. Math. Soc., vol. 49, n^o 2,‎ 2002, p. 182-192 (lire en ligne)
• Pierre Samuel, Théorie algébrique des nombres [détail de l’édition]
• Jean Trignan, Introduction aux problèmes d'approximation : fractions continues, différences finies, Éditions du Choix, 1994 (ISBN 978-2-90902816-3)
• Joan Gómez y Urgellés et Abel Gerschenfeld (Trad.), L'invention du langage arithmétique : Diophante, Barcelone, RBA Coleccionables, 2019, 157 p. (ISBN 978-84-473-9894-2). 

Développement d’un réel en fractions continues par M. Couchouron de l'université de Rennes I

• Arithmétique et théorie des nombres