Analyse de similitudes

La recherche en sciences sociales passe généralement par le recours à des catégories sociales ou des « classes sociales » déjà construites et prédéfinies par les chercheurs, sur la base d'attributs partagés : les « jeunes », les « cadres », les « pays », les « chômeurs », les « femmes », etc. Avec l'analyse de similitude, ces catégories ne sont pas fixées a priori mais rendues visibles par un ou des procédés qui permettent de classifier et de regrouper les cas analysés, selon leurs relations effectives — qui fait quoi, qui parle à qui, où, sur quoi, avec qui, etc..

La similarité en analyse de réseaux se produit quand deux sommets (ou plus, selon la structure analysée) se retrouvent dans la même classe d'équivalence. Dit autrement, des entités sociales ou des positions sociales d'une même classe d'équivalence se confondent sur la base des relations qu'ils entretiennent avec les autres, comme par exemple, des médecins qui ont des patients en suivi[1].

Il existe trois approches fondamentales afin de produire une mesure de similarité au sein d'un réseau : l'équivalence structurale, l'équivalence automorphique, et l'équivalence régulière[2]. Ces trois notions d'équivalence sont hiérarchisées : tout ensemble en équivalence structurale est également en équivalence automorphique et en équivalence régulière, tout ensemble en équivalence automorphique est en équivalence régulière, mais toutes les équivalences régulières ne sont pas nécessairement automorphiques ou structurales, et toutes les équivalences automorphiques ne sont nécessairement structurales[3].

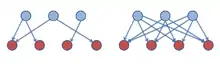
Deux sommets d'un réseau sont structurellement équivalents si leurs liens vers les autres sommets sont similaires.

Équivalence structurale

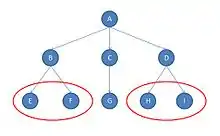
Dans l'image ci-proposée, aucun autre sommet (ou nœud) n'a exactement le même ensemble de liens que A qui appartient donc à une classe spécifique. Il en va de même pour les sommets B, C, D et G (chacun de ces sommets a son « ensemble » spécifique de liens vers d'autres sommets). Cependant, E et F, sont dans la même classe d'équivalence structurale, puisque tous les deux présentent le même schéma de liens (un lien vers B), ils sont dits en équivalence structurale. Il en va de même pour H et I, qui tous les deux présentent un lien vers D[3].

L'équivalence structurale est la plus forte forme de similarité. Dans la réalité, dans les réseaux sociaux l'équivalence pure est rare, et il est utile d'user de critères moins stricts afin de mesurer une équivalence approximative[4].

Un concept proche de celui de l'équivalence structurale est celui de l'équivalence institutionnelle : deux sommets (par exemple, deux entreprises) sont institutionnellement équivalentes si elles opèrent dans le même domaine institutionnel[5]. Alors que les sommets structurellement équivalents ont des schémas relationnels ou des positions de réseau identiques, l’équivalence institutionnelle reflète la similitude des influences institutionnelles que les sommets subissent dans les mêmes domaines et espaces, quelle que soit la similitude de leurs positions dans le réseau. Par exemple, deux banques de Chicago peuvent avoir des schémas de liens très différents (l’une peut être un sommet central et l’autre peut être en position périphérique), de sorte qu’elles ne sont pas des équivalents structuraux, mais parce qu’elles opèrent toutes deux sur le terrain de la finance et dans le même domaine défini géographiquement (Chicago), ils seront soumis aux mêmes influences institutionnelles[5].

Définition formelle par Karl Reitz et Douglas White (1989) : Soit ${\displaystyle X}$ un ensemble et ${\displaystyle R}$ une relation binaire dans ${\displaystyle X}$. ${\displaystyle E}$, relation d'équivalence, est une équivalence structurale, si et seulement si, pour tout ${\displaystyle a,b,c\in X}$ tel que ${\displaystyle a\neq c\neq b}$, ${\displaystyle a~E~b}$ implique[1] :

• ${\displaystyle a~R~b\Longleftrightarrow b~R~a}$, et
• ${\displaystyle a~R~c\Longleftrightarrow b~R~c}$, et
• ${\displaystyle c~R~a\Longleftrightarrow c~R~b}$, et
• ${\displaystyle a~R~a\Longleftrightarrow a~R~b}$

Formellement « Deux sommets sont automorphiquement équivalents si tous les sommets peuvent être renommés pour former un graphe isomorphique avec l'étiquette de ${\displaystyle U}$ et ${\displaystyle V}$ interchangés. Deux sommets équivalents automorphiquement partagent exactement les mêmes propriétés indépendantes de l'étiquette. »[7]

Plus intuitivement, des entités sociales sont en équivalence automorphique s'il est possible de permuter le graphe de façon que l'échange de deux entités n'ait aucun effet sur les distances entre les autres entités au sein du graphe.

Équivalence automorphique.

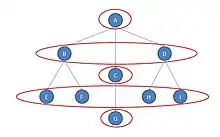
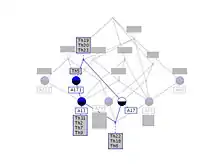
Dans l'image ci-contre, représentant une structure organisationnelle, A est au poste central, B, C et D répondent de A et agissent sur E, F et H, I ; G est isolé bien que répondant de C (et A). Bien que les acteurs B et D ne soient pas structurellement équivalents — ils ont le même répondant (A), mais pas les mêmes liens vers les autres —, ils semblent tout de même en équivalence. Les deux (B et D) répondent de A et sont en interaction avec deux entités (respectivement E F et H I). Si les sommets B et D étaient interchangés, ou encore, si on interchangeait E et H (ainsi que les autres combinaisons possibles) les distances entre les sommets dans le réseau resteraient exactement identiques. Il y a donc 5 classes d'équivalence automorphique dans ce graphe : ${\displaystyle \{A\}}$, ${\displaystyle \{B,D\}}$, ${\displaystyle \{C\}}$, ${\displaystyle \{E,F,H,I\}}$, et ${\displaystyle \{G\}}$. Il est à noter qu'une définition moins stricte de cette équivalence réduit le nombre de classes[3].

Définition formelle par Karl Reitz et Douglas White (1989) : Soit ${\displaystyle X}$ un ensemble, et ${\displaystyle R}$ une relation binaire dans ${\displaystyle X}$. ${\displaystyle E}$, relation d'équivalence, est une équivalence forte ou automorphique, si et seulement si, pour tout ${\displaystyle a,b,c,\in X}$, ${\displaystyle a~E~b}$ implique[1] :

• ${\displaystyle a~R~b\Longleftrightarrow b~R~a}$, et
• ${\displaystyle a~R~c\Longleftrightarrow b~R~c}$, et
• ${\displaystyle c~R~a\Longleftrightarrow c~R~b.}$

Formellement, « deux acteurs sont régulièrement équivalents s'ils sont également reliés à leurs équivalents ». En d'autres mots, des sommets régulièrement équivalents sont des sommets qui bien que ne partageant pas le même voisinage, partagent des voisinages qui sont eux-mêmes similaires[7].

Par exemple, deux mères sont équivalentes parce que chacune d'elles à un schéma de connexions relationnelles similaires avec son partenaire de couple, ses enfants, etc. Deux mères ne sont pas nécessairement liées au — ou à la — même partenaire, ni aux mêmes enfants, alors elles ne sont pas structuralement équivalentes. Et puisque que chaque mère peut avoir un nombre variable d'enfants et/ou de partenaires, elles ne sont pas non plus en équivalence automorphique. Mais elles sont similaires parce qu'elles ont le même type de relations avec d'autres ensembles d'entités sociales (elles aussi vues comme régulièrement équivalentes puisque similaires dans leurs types de liens vers l'entité "mère")[3].

Équivalence régulière

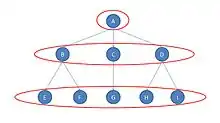
Dans le graphe présenté ci-contre, il y a trois classes d'équivalence régulière : ${\displaystyle \{A\}}$, ${\displaystyle \{B,C,D\}}$, ${\displaystyle \{E,F,G,H,I\}}$[3]

Définition formelle par Karl Reitz et Douglas White (1989) : Soit ${\displaystyle X}$ un ensemble, et ${\displaystyle R}$ une relation binaire dans ${\displaystyle X}$. ${\displaystyle E}$, relation d'équivalence, est une équivalence régulière, si et seulement si, pour tout ${\displaystyle a,b,c,\in X}$, ${\displaystyle a~E~b}$ implique[1] :

• ${\displaystyle a~R~c\Rightarrow \exists ~d\in X:b~R~d}$ et ${\displaystyle d~E~c}$, et
• ${\displaystyle c~R~a\Rightarrow \exists ~d\in X:d~R~b}$ et ${\displaystyle d~E~c}$

L'analyse de similitudes permet aux données de caractériser elles-mêmes leurs propres structures (comme par exemple, des cliques, des hiérarchies ou une équivalence), au lieu que chercheur détermine lui-même et a priori des catégories pour l'analyse, comme c'est généralement le cas en sciences sociales[1]. Ainsi, ce n'est pas le chercheur qui détermine les catégories sociales et qui en fait ou non partie, cela s'opère a posteriori des analyses de similitudes ; les cas soumis à l'analyse sont regroupés selon leurs attributs communs, ce qui permet de détecter des régularités (ou même des "irrégularités").

Interactions corrélatives

Sociologiquement, les "bleus" et les "rouges" sont deux identités sociales en interaction corrélative : où chacun des groupes jouent un rôle pour que l'interaction ait lieu : il pourrait s'agit du soin, de l'enseignement, ou du rapport de domination tel que décrit par Marx

En analyse de réseaux, les classes d'équivalence sont vues comme étant en interactions corrélatives ; "c’est-à-dire celles dans lesquelles les partenaires ne sont pas des individus semblables mis dans une situation particulière, mais des individus qui se définissent par le rôle qu’ils jouent dans l’interaction"[11]. Ensemble, ils produisent un fait social[11].

Les interactions corrélatives sont inégales d'un point de vue structurel, puisque les protagonistes ont des positions complémentaires dans l'interaction et la production du fait social : « Il s'agit d'une interaction qui dans son principe est dissymétrique »[1]. Cette notion permet de parler des rapports et des rôles sociaux[1].

Exemples d'interactions corrélatives :

• Soin : patient - médecin
• Enseignement : étudiant - enseignant
• Famille : enfant - parent
• Rapport de genre
• Rapport de classe
• Couple

Les méthodes d'analyse des similitudes relationnelles ne sont pas employées qu'en sciences sociales, c'est aussi un des procédés utilisés par la NSA[12], en forensique[13], en analyse automatique de large corpus, ou d'images[14], et aussi en biologie[15]^,[16]

• Théorie des réseaux

• Capital social

• Cohésion sociale
• Classe sociale
• Inégalité sociale
• Analyses de données
• Similarité (informatique)

• Alain Degenne et Pierre Vergès, « Introduction à l'analyse de similitude », Revue française de sociologie, vol. 14, n^o 4,‎ 1973, p. 471-511 (DOI 10.2307/3320247, lire en ligne).
• Bouriche Boumedine, « L'analyse de similitude », dans Jean-Claude Abric (dir.), Méthodes d'étude des représentations sociales, ERES, 2005, 296 p. (ISBN 9782749201238, présentation en ligne), p. 221-252.

• (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Similarity (network science) » (voir la liste des auteurs).

• Portail de la sociologie
• Portail des probabilités et de la statistique
• Portail des données
• Portail de l'informatique théorique