Chimiométrie
La chimiométrie est l'application d'outils mathématiques, en particulier statistiques, pour obtenir le maximum d'informations à partir de données chimiques[1],[2].
| Sous-classe de | |
|---|---|
| Pratiqué par |
Chemometrician (d) |
La chimiométrie est une discipline très appliquée. Son objectif est d'améliorer le contrôle et l'optimisation des procédés ainsi que la qualité des produits fabriqués. Son développement a été fortement accéléré par celui de la spectrométrie proche infrarouge dans les laboratoires de chimie analytique[3].
La chimiométrie se distingue des statistiques par le fait que :
- les statistiques requièrent que des hypothèses soient vérifiées a priori. Par exemple on vérifie l’indépendance et la distribution des variables avant de réaliser une régression linéaire ;
- la chimiométrie néglige ces précautions, car elles sont irréalisables sur les données qu’elle traite, mais procède à des vérifications a posteriori, sur la qualité des structures construites ou sur les performances des modèles.
La chimiométrie regroupe notamment[4] :
- les méthodes multivariées d'analyse de données ;
- les méthodes de régression multivariée ;
- Les méthodes de discrimination et de classification ;
- les méthodes de prétraitement du signal ;
- la validation des méthodes de mesure ;
- les plans d'expérience.
Les plans d'expériences ont pour objectif d'organiser mathématiquement les conditions expérimentales pour choisir les plus informatives, ce qui permet de minimiser le nombre d'expériences tout en maximisant l'information obtenue.
Données étudiées
L'une des grandes aires d'application de la chimiométrie est la spectroscopie infrarouge : proche et moyen infra-rouge (PIR/MIR)[5] sous différentes approches (multi/hyperspectral, spatial ou non). Mais d'autres données peuvent également être étudiées : spectroscopie RMN[6], spectroscopie de masse[7], spectroscopie Raman[8].
Les signaux traités par la chimiométrie ont généralement en commun que chaque variable (chaque intensité à une longueur d'onde données d'un spectre) est peu sensible vis à vis du phénomène étudié, mais l'ensemble des variables peut l'être. La chimiométrie, via des opérations d'algèbre linéaire, consiste alors à combiner les variables du signal, peu sensibles, pour créer de nouvelles variables appelées variables latentes, plus sensibles[9].
Méthodologie générale et bonnes pratiques
Notations
Les matrices seront représentées par des majuscules grasses, comme X. Les vecteurs, par des minuscules grasses, comme xj qui représente la j ième colonne de X, et les scalaires, par des minuscules italiques, comme n indiquant le nombre d'individus ou p indiquant le nombre de variables. Les données contenant les signaux décrits par p variables mesurées sur n individus seront rangées dans une matrice X de n lignes par p colonnes[10].
Apprentissage
Un grand nombre de méthodes chimiométriques ont pour but de réaliser un étalonnage (calibration en anglais), entre un signal x (par exemple un spectre) et des grandeurs à prédire y (par exemple une concentration et une densité), au moyen d'un apprentissage. En apprentissage, on cherche à construire un modèle mathématique à partir d'un ensemble d'échantillons sur lesquels on aura mesuré x et y, regroupés dans deux matrices, X et Y. Pour ce faire, les données sont classiquement séparées en 3 groupes : le jeu d'apprentissage (Xc, Yc), le jeu de validation (Xv, Yv) et le jeu de test (Xt, Yt)[11].
Il y a deux phases dans la construction d'un modèle.
- Une phase d'optimisation des (hyper-)paramètres du modèle (le prétraitement du signal, le nombre de plus proches voisins pour le kNN, le nombre de variables latentes dans une PLS, etc.). Un modèle est calculé sur Xc, Yc avec des valeurs de paramètres données et le modèle est ensuite testé sur Xv, Yv. Le résultat de ces tests permet de régler les paramètres du modèle.
- Une phase d'évaluation du modèle. Un modèle utilisant les paramètres déterminés à la phase d'optimisation est calculé sur (Xc+Xv, Yc+Yv) et testé sur Xt, Yt.
La phase 1 emprunte généralement une validation croisée, dans laquelle l'ensemble d'étalonnage et l'ensemble de validation sont tirés de manière répétée. Plusieurs types de validation croisée existent : random blocs, jack-knife, venitian blind, leave-one-out, répétée... Le leave-one-out n'est pas recommandé car il favorise le sur-apprentissage. La validation croisée répétée est préférable.
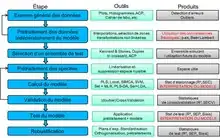
Pendant la construction du modèle, on doit attacher une grande importance à ne pas biaiser artificiellement ses critères de performances. Par exemple, tous les réplicats de mesures d'un même échantillon ne doivent jamais être séparés entre le jeu d'étalonnage et le jeu de validation, et le jeu test doit être le plus indépendant possible et représentatif de l'utilisation future du modèle.
Le schéma représente le logigramme typique de la construction d'un modèle d'étalonnage en chimiométrie.
Critères de performance et d'évaluation des modèles
Les critères employés pour l'évaluation de la performance : RMSEP, le R2 (et/ou le RPD qui est relié au R2).
Les critères employés pour l'évaluation de la qualité : coefficient de Durbin-Watson, le T2 d'Hoteling, le coefficient Q.
Techniques et méthodes employées
Pré-traitement des données
Avant d'être traitées par les méthodes d'exploration ou d'étalonnage, les données ont parfois besoin d'être pré-traitées, afin d'éliminer des signaux de fond indésirables, comme par exemple les effets des réflexions spéculaires en spectroscopie. Beaucoup de méthodes de prétraitement ont été imaginées et développées, tant pour gommer des altérations génériques, comme par exemple les effets multiplicatifs ou additifs[12], que pour résoudre des problèmes spécifiques à chaque technique analytique, comme par exemple la fluorescence en spectrométrie Raman[13].
Les prétraitements se classent en deux grandes catégories : les prétraitements basés sur des statistiques calculées sur les individus de la base de données (c’est-à-dire sur les colonnes de la matrice) et les prétraitements basés sur le traitement du signal de chaque individu (c’est-à-dire sur les lignes de la matrice).
Prétraitements basés sur les statistiques des colonnes
La chimiométrie repose essentiellement sur des calculs statistiques tels que la moyenne, la variance, la covariance, etc. Ces quantités caractérisent l'ensemble des individus sur lesquels le modèle sera construit. Par exemple, une PLS cherche à maximiser la covariance. Toutefois, les unités utilisées pour mesurer les variables peuvent avoir des échelles non comparables. De même, la distribution de certaines variables peut être très asymétrique, ce qui entraîne des biais dans les estimations des moments statistiques. Un certain nombre de prétraitements sont consacrés à la correction de ces distorsions. Les prétraitements basés sur les statistiques des colonnes sont calculés dans l'espace des individus et sont ensuite appliqués sur chaque individu testé par le modèle. Par conséquent ils ne doivent pas être effectués avant le fractionnement de l'ensemble étalonnage / test. Une attention particulière doit également être portée lors de la validation croisée. En effet, le prétraitement doit être "intégré" dans la boucle de validation croisée afin de le calculer et de l'appliquer à chaque itération de la validation croisée.
Les méthodes les plus courantes pour corriger la distribution des variables consistent à soustraire et/ou diviser chaque colonne par une statistique calculée sur cette colonne.
Centrage par colonne
Le centrage par colonne a pour but de définir l'origine par laquelle passe le modèle. Une description détaillée des différents modes de centrage se trouve dans Bro et Smilde[14]. Dans le plus courant, la moyenne de chaque colonne de données est soustraite de toutes les valeurs de cette colonne pour donner une matrice de données où la moyenne de chaque variable pré-traitée est nulle. Lorsque le modèle, calculé sur ces données pré-traitées, est appliqué à un nouvel individu, il faut appliquer à cet individu le même centrage que celui utilisé par le prétraitement, c'est-à-dire soustraire à cet individu la moyenne du jeu d'étalonnage.
Normalisation par colonne
La normalisation des colonnes a pour but d'équilibrer les poids statistiques de toutes les colonnes. Cela revient à rendre les colonnes a-dimensionnelles. Il existe différentes méthodes pour cela. La plus courante consiste à donner la même variance à toutes les colonnes, en les divisant par leur écart-type, après les avoir centrées. Cela signifie que la seule information qui reste est liée aux corrélations entre les variables. Cette opération est appelée également réduction ou autoscaling. D'autres statistiques que l'écart-type peuvent être utilisées, comme par exemple la racine carrée de l'écart-type, dans le Pareto Scaling.
Très rarement utilisé en spectrométrie proche infrarouge, l'autoscaling est très utile lorsque les signaux porteurs d'information sont faibles et non corrélés à d'autres signaux plus forts. Ces cas peuvent se produire par exemple avec des signaux de spectrométrie de masse.
Prétraitements basés sur le traitement du signal
Les méthodes de traitement du signal sont largement utilisées pour des applications spectroscopiques, afin de corriger les données spectrales des effets de taille et de se concentrer sur la forme du signal. Contrairement aux méthodes basées sur les statistiques des colonnes, les prétraitements basés sur le signal s'appliquent à chaque individu, indépendamment des autres. Ils peuvent donc en général être effectués avant le fractionnement des ensembles d'étalonnage et de test et ne nécessitent aucune précaution en ce qui concerne la validation croisée.
Correction des lignes de base
Les spectres peuvent contenir des signaux d'arrière-plan structurés qui sont généralement appelés lignes de base. Les lignes de base sont censées être des signaux continus et à basse fréquence qui s’ajoutent au signal mesuré. Il existe différents modèles de ligne de base : constante, linéaire, polynomiale, etc. qui ont donné lieu à différentes méthodes de correction. De plus, certains filtres de traitement du signal ont été adaptés au prétraitement des spectres chimiométriques. Il y a donc beaucoup de méthodes, le choix de la meilleure dépend fortement de l'application[15].
Les méthodes de correction de ligne de base les plus courantes sont :
- la soustraction d'une valeur à tout le spectre. Par exemple en soustrayant le minimum, le spectre pré-traité aura un minimum égal à 0. Cette méthode n'est pas conseillée, car elle utilise la valeur d'un seul point et a donc tendance à augmenter le bruit du spectre. De plus, cette méthode ne corrige que des lignes de base horizontales.
- la soustraction de la moyenne du spectre à tout le spectre. De la sorte, le spectre résultant a une moyenne nulle. Cette méthode est préférable à la précédente parce qu'elle propage moins de bruit, utilisant une valeur calculée à partir de tous les points. Par contre elle ne corrige que des lignes de base horizontales et produit des spectres avec des valeurs négatives, ce qui peut être gênant pour l'application de certaines méthodes.
- la soustraction d'une ligne calculée sur une partie du spectre. Si, par expertise, on sait qu'une zone du spectre devrait être nulle, ou qu'en deux points distants, le signal devrait être nul, alors il suffit de calculer l'équation de la droite passant par cette zone ou par les deux points et de la soustraire du spectre.
- le "detrending" permet d'enlever la tendance globale sous-jacente au spectre. Une régression est calculée entre les abscisses et le spectre, avec un modèle de type constant (degré 0), linéaire (degré 1), ou polynomial (degré ≥ 2). La courbe de tendance trouvée est enlevée du spectre. On remarquera que le detrend de degré 0 n'est rien d'autre que la soustraction de la moyenne. On remarquera également qu'un detrend de degré k est une projection orthogonale à l'espace des polynômes de degré k[16]. Detrend permet d'enlever des lignes de bases plus complexes qu'une simple droite, mais produit des valeurs négatives, ce qui peut être gênant pour l'application de certaines méthodes.
- La méthode ALS, pour Asymmetric Least Squares, identifie la ligne de base d'un spectre avec une régression des moindres carrés pénalisés. L'idée est de trouver le signal qui s'approche le mieux du spectre, au sens des moindres carrés, tout en ayant un aspect lisse, au sens d'un critère de fréquence. Cette méthode est particulièrement utile en spectrométrie Raman pour enlever les lignes de bases dues à la fluorescence.
Correction de l'échelle (scaling)
Un signal mesuré x peut être affecté par un effet multiplicatif, ce qui signifie que ax peut être mesuré au lieu de x, avec a ≠ 1. Dans le domaine de la chromatographie, l'effet multiplicatif peut être dû à la quantité de produit analysé. Dans le domaine de la RMN, la dilution du produit analysé est responsable de l'effet multiplicatif. Dans le domaine du PIR, l'effet multiplicatif peut être dû à la géométrie de l'appareil de mesure ou à la taille des particules du produit. L'effet multiplicatif est incompatible avec les outils de l'algèbre linéaire. En effet, tout traitement de x par l'algèbre linéaire aboutit à une ou plusieurs opérations matricielles comme, par exemple, t = xTP, où P est une matrice de loadings. Si x est multiplié par a, le résultat t sera également multiplié par a. En d'autres termes, les effets multiplicatifs passent à travers les modèles linéaires.
L'effet multiplicatif peut être traité en appliquant un logarithme au signal mesuré. Il faut pour cela qu'aucun autre effet tel qu'une ligne de base ne soit inclus dans le signal à traiter.
L'utilisation de la normalisation est plus courante. La normalisation consiste à diviser toutes les variables du signal x par une fonction d de x, de telle sorte que d(ax) = ad(x). Ainsi, chaque ax conduira au même signal corrigé z = ax/d(ax) = x/d(x), quelle que soit la valeur de a. Bien que des méthodes de normalisation spectrale soient appliquées à chaque spectre individuel, certaines d'entre elles nécessitent l'ensemble des données pour calculer les facteurs de correction ; dans ce cas, le prétraitement ne doit pas être effectué avant la définition des ensembles d'étalonnage et de test et une attention doit également être portée en effectuant une validation croisée. Il existe différentes méthodes de normalisation :
- La normalisation par le maximum consiste à diviser toutes les valeurs du spectre par son maximum. L'implémentation de cette normalisation est très simple. Mais elle est déconseillée car, en n'utilisant qu'une seule valeur pour estimer l'effet multiplicatif, elle propage du bruit sur le spectre.
- La normalisation par la gamme consiste à diviser toutes les valeurs du spectre par la différence de signal entre deux points spécifiques du spectre, ou par la différence entre le maximum et le minimum. Cette méthode présente l’avantage de ne pas baser l’évaluation de l’effet multiplicatif sur une seule valeur.
- La normalisation par la norme du spectre consiste à diviser toutes les valeurs du spectre par la moyenne quadratique de toutes les valeurs du spectre. Cette méthode présente l’avantage de baser l’évaluation de l’effet multiplicatif sur une statistique très stable et donc de ne pas augmenter le bruit.
- Lorsque l’effet multiplicatif est estimé en utilisant toutes les variables du signal, l’information portée par les pics (reliés à la chimie) se dilue sur l’ensemble du spectre[17]. Probalistic Quotient Normalization (PQN) a été développée pour répondre à ce problème. Elle consiste à :
- calculer le coefficient multiplicatif a entre chaque valeur du spectre à traiter et la valeur correspondante d'un spectre de référence.
- retenir la valeur la plus fréquente du coefficient multiplicateur
Correction combinée de la ligne de base et de l'échelle
Les méthodes combinant la réduction de ligne de base et la mise à l'échelle des spectres sont très utilisées. Ainsi :
- Standard Normal Variate (SNV) [18] enlève au spectre son intensité moyenne et le divise ensuite par son écart type. Cette méthode est également appelée, à juste titre, centrage réduction en ligne.
- Multiplicative Scatter Correction (MSC) [12] identifie l'effet additif et l'effet multiplicatif de chaque spectre, en comparaison à un spectre de référence, puis le corrige explicitement :
- calcul de et tels que
- correction de :
- Extended Multiplicative Signal Correction (EMSC) [19] procède comme MSC, mais avec des modèles de lignes de base plus complexe qu'une simple constante.
De la même manière que pour les méthodes de scaling, les méthodes SNV et MSC ont tendance à diluer les zones porteuses d'information, comme les pics chimiques, sur l'ensemble des spectres. Ce problème est connu sous le nom de fermeture (closure en anglais) [20]. Pour pallier ce problème, différentes méthodes alternatives ont été proposées [21],[22]. Elles reposent toutes sur l'idée d'estimer les effets additifs et multiplicatifs sur les parties des spectres affectées seulement par ces effets.
Analyse de données (EDA) : méthodes non supervisées
Les méthodes non-supervisées ont pour but d'explorer un jeu de données, en mettant en avant les sources principales de variabilité, et en définissant les groupes formés par les échantillons.
ACP
Spécificité de l'ACP dans le cadre de la SPIR est de représenter les loadings de chaque composantes principales sous forme de spectre.
Autres méthodes
CANDECOMP/PARAFAC (en)[style à revoir]
Non linéaires
PLS locale (LWPLS, local PLS), ANN, CNN, SVM
Linéaires
PLS-DA
Non linéaires
kNN, CAH, RF, SVM
Multivariate Curve Resolution - Asymmetric Least Squares (MCR-ALS)
SIMPLEX
Méthode traitement signal
ICA
Méthodes issues de la télédétection
SIMPLEX
Méthodes particulièrement adaptées aux spectres
CovSel, VIP, UVE
Détection de points atypiques dans le multi-varié
Utilisation du T2 et Q
Quelques exemples d'applications
Utilisation de la SPIR pour caractériser des matières complexes (plantes, aliments, déchets organiques, sols)
- Différentes caractéristiques sont prédites sur les céréales et graines : la teneur en protéines, composition en acides aminés ou acides gras (voir les dernières publications dans ce domaine ici).
- Différentes caractéristiques sont également prédites sur les sols[23] : matière organique, texture, minéraux, CEC, matière sèche, pH, contaminations (voir les dernières publications dans ce domaine ici).
- Le FlashBMP[24],[25] a été développé pour prédire le potentiel biochimique de méthane (BMP) sur divers déchets organiques destinés à la méthanisation (boues urbaines, déchets agro-alimentaire, déchets cantine). L'application nécessite aujourd'hui une étape de lyophilisation et broyage de la matière.
Références
- (en) Svante Wold, « Chemometrics; what do we mean with it, and what do we want from it? », Chemometrics and Intelligent Laboratory Systems, vol. 30, no 1, , p. 109–115 (ISSN 0169-7439, DOI 10.1016/0169-7439(95)00042-9, lire en ligne, consulté le )
- (en) Kim Esbensen et Paul Geladi, « The start and early history of chemometrics: Selected interviews. Part 2 », Journal of Chemometrics, vol. 4, no 6, , p. 389–412 (ISSN 0886-9383 et 1099-128X, DOI 10.1002/cem.1180040604, lire en ligne, consulté le )
- (en) H. M. Heise et R. Winzen, « Chemometrics in Near-Infrared Spectroscopy », dans Near-Infrared Spectroscopy, Wiley-VCH Verlag GmbH (ISBN 9783527612666, lire en ligne), p. 125–162
- (en) Comprehensive Chemometrics : chemical and biochemical data analysis, Amsterdam, Elsevier, (ISBN 978-0-444-52701-1, lire en ligne)
- http://math.agrocampus-ouest.fr/infoglueDeliverLive/digitalAssets/41740_Poly_Bertrand_2008.pdf
- https://tel.archives-ouvertes.fr/tel-01341959/document
- https://tel.archives-ouvertes.fr/tel-00685887/document
- https://serval.unil.ch/resource/serval:BIB_DD70B27E1A48.P003/REF.pdf
- https://agritrop.cirad.fr/567909/1/document_567909.pdf
- Carl Meyer, Matrix Analysis and Applied Linear Algebra, SIAM, , 718 p. (ISBN 978-0-89871-454-8, lire en ligne)
- B.G.M. Vandeginste, D.L. Massart, L.M.C. Buydens et S. De Jong, « Introduction to Part B », dans Data Handling in Science and Technology, Elsevier, (ISBN 978-0-444-82853-8, lire en ligne), p. 1–5
- Tomas Isaksson et Tormod Næs, « The Effect of Multiplicative Scatter Correction (MSC) and Linearity Improvement in NIR Spectroscopy », Applied Spectroscopy, vol. 42, no 7, , p. 1273–1284 (ISSN 0003-7028 et 1943-3530, DOI 10.1366/0003702884429869, lire en ligne, consulté le )
- Nils Kristian Afseth, Vegard Herman Segtnan et Jens Petter Wold, « Raman Spectra of Biological Samples: A Study of Preprocessing Methods », Applied Spectroscopy, vol. 60, no 12, , p. 1358–1367 (ISSN 0003-7028 et 1943-3530, DOI 10.1366/000370206779321454, lire en ligne, consulté le )
- Rasmus Bro et Age K. Smilde, « Centering and scaling in component analysis », Journal of Chemometrics, vol. 17, no 1, , p. 16–33 (ISSN 0886-9383 et 1099-128X, DOI 10.1002/cem.773, lire en ligne, consulté le )
- Kristian Hovde Liland, Trygve Almøy et Bjørn-Helge Mevik, « Optimal Choice of Baseline Correction for Multivariate Calibration of Spectra », Applied Spectroscopy, vol. 64, no 9, , p. 1007–1016 (ISSN 0003-7028 et 1943-3530, DOI 10.1366/000370210792434350, lire en ligne, consulté le )
- Jean-Claude Boulet et Jean-Michel Roger, « Pretreatments by means of orthogonal projections », Chemometrics and Intelligent Laboratory Systems, vol. 117, , p. 61–69 (ISSN 0169-7439, DOI 10.1016/j.chemolab.2012.02.002, lire en ligne, consulté le )
- Gilles Rabatel, Federico Marini, Beata Walczak et Jean‐Michel Roger, « VSN: Variable sorting for normalization », Journal of Chemometrics, (ISSN 0886-9383 et 1099-128X, DOI 10.1002/cem.3164, lire en ligne, consulté le )
- R. J. Barnes, M. S. Dhanoa et Susan J. Lister, « Standard Normal Variate Transformation and De-Trending of Near-Infrared Diffuse Reflectance Spectra », Applied Spectroscopy, vol. 43, no 5, , p. 772–777 (ISSN 0003-7028 et 1943-3530, DOI 10.1366/0003702894202201, lire en ligne, consulté le )
- Harald Martens et Edward Stark, « Extended multiplicative signal correction and spectral interference subtraction: New preprocessing methods for near infrared spectroscopy », Journal of Pharmaceutical and Biomedical Analysis, vol. 9, no 8, , p. 625–635 (ISSN 0731-7085, DOI 10.1016/0731-7085(91)80188-f, lire en ligne, consulté le )
- M. Bylesjö, O. Cloarec et M. Rantalainen, « Normalization and Closure », dans Comprehensive Chemometrics, Elsevier, (ISBN 978-0-444-52701-1, lire en ligne), p. 109–127
- Q Guo, W Wu et D.L Massart, « The robust normal variate transform for pattern recognition with near-infrared data », Analytica Chimica Acta, vol. 382, nos 1-2, , p. 87–103 (ISSN 0003-2670, DOI 10.1016/s0003-2670(98)00737-5, lire en ligne, consulté le )
- Gilles Rabatel, Federico Marini, Beata Walczak et Jean‐Michel Roger, « VSN: Variable sorting for normalization », Journal of Chemometrics, (ISSN 0886-9383 et 1099-128X, DOI 10.1002/cem.3164, lire en ligne, consulté le )
- Bo Stenberg, Raphael A. Viscarra Rossel, Abdul Mounem Mouazen et Johanna Wetterlind, « Chapter Five - Visible and Near Infrared Spectroscopy in Soil Science », dans Advances in Agronomy, vol. 107, Academic Press, (DOI 10.1016/s0065-2113(10)07005-7, lire en ligne), p. 163–215
- « Méthodes de Chimiométrie et Machine Learning / Ondalys », sur Ondalys (consulté le ).
- M. Lesteur, E. Latrille, V. Bellon Maurel et J. M. Roger, « First step towards a fast analytical method for the determination of Biochemical Methane Potential of solid wastes by near infrared spectroscopy », Bioresource Technology, vol. 102, no 3, , p. 2280–2288 (ISSN 0960-8524, DOI 10.1016/j.biortech.2010.10.044, lire en ligne, consulté le )
- Portail de la chimie