Demi-vie

En biologie, la demi-vie d'une enzyme correspond au temps nécessaire pour que l'enzyme perde la moitié de son activité spécifique pour cause de dénaturation et d'inactivation.

En pharmacologie, la demi-vie désigne par extension le temps nécessaire pour que la concentration d’une substance contenue dans un système biologique soit diminuée de la moitié de sa valeur initiale (par exemple la concentration d’un médicament dans le plasma sanguin).

Ce paramètre varie légèrement d'un individu à l'autre, selon le processus d'élimination et le fonctionnement relatif chez l'individu.

En pratique, on considère qu'un médicament n'a plus d'effet pharmacologique après cinq à sept demi-vies.

Pour une réaction chimique, la notion de demi-vie est appelée temps de demi-réaction.

Dans un cas simple, par exemple pour la réaction d'équation A → P, la définition donnée ci-dessus du temps de demi-vie s'applique parfaitement au temps de demi-réaction. En revanche, dans le cas général, cette définition est incorrecte comme le montrent les deux exemples suivants :

• cas de la réaction d'équation A + B → P avec, comme conditions initiales sur les quantités de matière, n(A) = 10 mol et n(B) = 1 mol. Quand le temps de demi-vie est atteint, la quantité restant de A n'est pas n(A)/2, qui vaudrait 5 mol, mais n(A) = 9,5 mol ;
• cas de la réaction équilibrée A = P de constante d'équilibre K = 0,25 avec la condition initiale n(A) = 10 mol et n(P) = 0 mol. A l'équilibre, n(A)_éq = 8 mol et n(P)_éq = 2 mol. Le temps de demi-réaction est le temps au bout duquel n(A) = 9 mol (et non le temps au bout duquel n(A) = 5 mol, situation qui n'arrivera jamais dans ce cas).

Ces deux exemples montrent qu'il faut une autre définition du temps de demi-réaction, que celle donnée pour le temps de demi-vie. La définition généralement donnée est : "Le temps de demi-réaction est le temps au bout duquel la moitié de l'avancement final est atteint". En termes moins scientifiques, c'est le temps au bout duquel la moitié de l'évolution possible est atteinte, ou encore, le temps pour lequel la moitié de ce qui doit se faire est fait.

L'IUPAC donne la définition suivante[1]

« For a given reaction the half life t1/2 of a reactant is the time required for its concentration to reach a value that is the arithmetic mean of its initial and final (equilibrium) values. »

Pour une réaction donnée, le temps de demi-réaction t1/2 d'un réactif est le temps pour lequel sa concentration atteint la valeur qui est la moyenne arithmétique entre sa concentration à l'état initial et celle à l'état final (à l'équilibre).

Le cas des réactions d'ordre 1 est intéressant car le temps de demi-réaction est indépendant des conditions initiales. La loi de vitesse (pour l'équation A → P) est

vitesse = -d[A] / dt = k[A] (ou k est la constante de vitesse)

Le temps de demi-réaction est τ_1/2 = ln(2) / k

Le fait que le temps de demi-réaction est indépendant de la concentration initiale est caractéristique de l'ordre 1.

Les réactions qui ne sont pas d'ordre 1 ont toutes un temps de demi-réaction qui dépend de la concentration initiale.

• Cas de l'ordre 2

Le temps de demi-réaction, dans le cas des cinétiques d'ordre 2, dont la loi de vitesse est de la forme

vitesse de réaction = k [A]²

le temps de demi-réaction est τ_1/2 = [A]₀ / k

• Cas de l'ordre 0

Le temps de demi-réaction, dans le cas des cinétiques d'ordre 0, dont la loi de vitesse est de la forme

vitesse de réaction = k

le temps de demi-réaction est τ_1/2 = [A]₀ / 2k

Le cas de certaines molécules qui présentent une faible stabilité et qui se décomposent, généralement en se transformant en d'autres espèces moléculaires, se traduit par l'équation A → P. Dans ce cas, la définition de la demi-vie est équivalente à la définition mettant en jeu l'avancement. Cette décomposition n'est pas instantanée mais fait décroître la quantité de molécules en fonction du temps, le temps de demi-réaction caractérise cette décroissance en indiquant la durée au bout de laquelle la quantité de molécules est diminuée de moitié. Cette demi-vie moléculaire dépend de la température.

En physique, la demi-vie (ou période) d'un isotope radioactif est le temps au bout duquel la moitié des noyaux de cet isotope initialement présents se sont désintégrés. S'il n'y a pas par ailleurs de création de tels noyaux (comme produits d'une réaction nucléaire ou de la désintégration d'autres radioisotopes), c'est aussi le temps au bout duquel le nombre de noyaux de l'isotope considéré a été divisé par deux.

Demi-vie (médiane) et durée de vie moyenne (espérance) d'une population ayant une décroissance exponentielle.

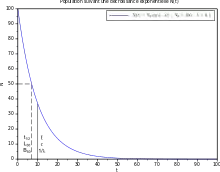
La désintégration d'une particule est « totalement aléatoire », c'est-à-dire que sa probabilité de désintégration est uniforme dans l'avenir, et ne dépend que de la durée de l'intervalle d'avenir considéré. Le taux de proportionnalité temporel est noté ${\displaystyle \lambda }$. La probabilité pour la particule de se désintégrer entre les instants futurs ${\displaystyle t}$ et ${\displaystyle t+\mathrm {d} t}$ vaut donc :

${\displaystyle \operatorname {Prob} ({\text{désintégration dans}}~[t~;~t+\mathrm {d} t])=\lambda \,\mathrm {d} t}$

C'est également la probabilité que la durée de vie ${\displaystyle T}$ d'une particule soit égale à ${\displaystyle t}$ (puisqu'elle existe à l'instant ${\displaystyle t}$ et n'existe plus à ${\displaystyle t+\mathrm {d} t}$) :

${\displaystyle \operatorname {Prob} (T\in [t~;~t+\mathrm {d} t[\,)=\lambda \,\mathrm {d} t}$

Ceci décrit également les systèmes présentant un taux de défaillance instantané constant, c'est-à-dire une défaillance sans faiblesse de jeunesse, ni usure, ni effet de mémoire, comme les composants électroniques.

À l'échelle d'une population de ${\displaystyle N}$ particules (ou systèmes), la loi de désintégration (ou de défaillance) s'écrit donc :

${\displaystyle {\mathrm {d} N(t) \over \mathrm {d} t}=-\lambda \,N(t)}$[alpha 2]

où :

${\displaystyle N(t)}$ est la population à l'instant ${\displaystyle t}$ ;

${\displaystyle \lambda }$ (lettre grecque lambda) est une constante homogène à l'inverse d'un temps (elle s'exprime en s⁻¹, a⁻¹, etc.) ; dans le contexte de la radioactivité on l'appelle constante de désintégration.

La résolution de cette équation différentielle fait apparaître une fonction exponentielle décroissante :

${\displaystyle N(t)=N_{0}\;\mathrm {e} ^{-\lambda t}}$ dans lequel ${\displaystyle N_{0}}$ est la concentration au temps initial.

La demi-vie (notée ${\displaystyle t_{1/2}}$) est définie comme étant l'instant tel que l'on ait :

${\displaystyle N(t_{1/2})={1 \over 2}N_{0}}$

On a donc :

${\displaystyle t_{1/2}={\ln(2) \over \lambda }}$

Si ${\displaystyle T}$ est la durée de vie d'une particule, on a également, par simple application de la définition des probabilités donnée ci-dessus :

${\displaystyle Prob(T\;\leqslant \;t_{1/2})=Prob(T\;\geqslant \;t_{1/2})={1 \over 2}}$

Remarque importante : La durée de vie moyenne de la particule - notée : ${\displaystyle T_{moy}}$ - n'est pas à confondre avec la demi-vie, notée : ${\displaystyle t_{1/2}}$

${\displaystyle T_{moy}={1 \over \lambda }={t_{1/2} \over \ln(2)}}$

Tous les systèmes ne suivent pas une loi exponentielle. En particulier, le taux de défaillance instantané n'a aucune raison d'être uniforme :

• il peut décroître, ce qui indique que le système devient plus robuste avec le temps ou bien que les systèmes présentant des défauts de jeunesse sont éliminés dans les premiers temps (voir Mortalité infantile, Mortalité juvénile et Rodage) ;
• il peut croître, ce qui indique un phénomène de vieillissement, d'usure ;
• il peut avoir une courbe « en baignoire », avec trois étapes dans la vie du système : décroissant, puis constant, puis croissant.

Dans tous les cas, la demi-vie t_1/2 reste égale à la médiane.

Durées de vie moyennes et demi-vies pour diverses lois statistiques continues

Loi	Fonction de survie R(t ) = N(t )/N0[alpha 3]	Durée de vie moyenne τ = t	Durée de demi-vie t1/2 = L50 = B50
Exponentielle	exp(-λt)	1/λ	ln(2)/λ
Normale	${\displaystyle 1-\Phi \left({\frac {t-\mu }{\sigma }}\right)}$	μ	μ
Log-normale	${\displaystyle 1-\Phi \left({\frac {\ln t-\mu }{\sigma }}\right)}$	exp(μ + σ2/2)	exp(μ)
Weibull	${\displaystyle \exp \left(-(t/\lambda )^{\beta }\right)}$	λΓ(1 + 1/β)	λln(2)1/β
Χ2	${\displaystyle {\frac {\gamma (k/2,t/2)}{\Gamma (k/2)}}}$	k	≈ k - 2/3
Logistique	${\displaystyle {\frac {1}{1+\exp \left({\frac {x-\mu }{s}}\right)}}}$	μ	μ
Log-logistique	${\displaystyle {\frac {\alpha ^{\beta }}{t^{\beta }+\alpha ^{\beta }}}}$	${\displaystyle {\frac {\alpha \pi }{\beta \sin(\pi /\beta )}}}$	α

• Période radioactive, Décroissance radioactive
• Période biologique
• Décroissance exponentielle
• Distribution exponentielle
• Temps de doublement, la notion contraire
• Température de demi-vie
• Loi de fiabilité

• (Histoire des sciences) L'article de Rutherford et Soddy (1903) mettant en évidence la demi-vie radioactive, site BibNum.

• Portail de la physique
• Portail de la chimie
• Portail de la protection des cultures