Ellipsographe
Un ellipsographe est un instrument mécanique permettant de tracer des ellipses d'un mouvement continu. Outre l'outil très simple qu'est la corde du jardinier, on distingue, parmi les ellipsographes, les systèmes articulés plans appelés trammels et les systèmes en dimension trois comme les compas. Nombreux sont les mathématiciens ayant donné leur nom à un ellipsographe exploitant une propriété particulière des ellipses.
Systèmes articulés
Ellipsographe d'Archimède
Selon Dominique Raynaud, l'attribution de cet ellipsographe à Archimède est sans fondement[1]. Il est parfois attribué à Proclus[2] car la propriété utilisée est citée par Proclus dans son commentaire d'Euclide[1]. Sa construction par le Marquis de L'Hôpital, en 1707[1], est attestée : le musée d'histoire des sciences de Florence en possède un exemplaire[3].
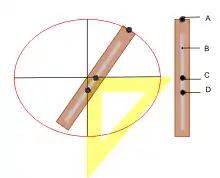
Cet ellipsographe s'appuie sur la propriété suivante : si on considère un segment [AD] de longueur a et un point C sur le segment [AD] tel que AC=b, le lieu des points A quand les points C et D se déplacent respectivement sur deux droites perpendiculaires est une ellipse de demi-axes a et b.
En effet, si on note θ l'angle , les coordonnées (x,y) du point A vérifient les conditions :
qui est l'équation paramétrée d'une ellipse.
Il n'est pas nécessaire que les axes soient perpendiculaires pour dessiner une ellipse[4].
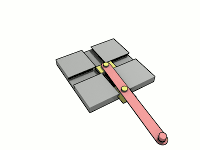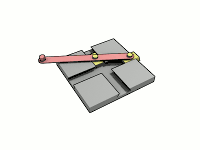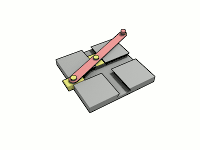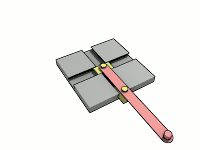
Gaston Tissandier propose une version simple d'un tel ellipsographe[5] : il suffit d'une simple équerre et d'une règle dans laquelle a été creusée une rainure (B), on munit la règle d'une pointe traceuse (A) et de deux vis coulissantes(C et D), on place les vis telles que AC=b et AD=a, puis on fait pivoter la règle de telle sorte que les vis restent toujours en contact avec les côtés de l'équerre, la pointe traceuse dessine alors l'ellipse de demi-axes a et b, après 4 placements de l'équerre.
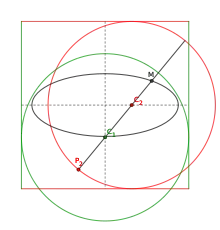
La réalisation pratique d'ellipses par cette méthode présente deux inconvénients:
- Le système de guidage des points C et D peut donner des imprécisions qui risquent de conduire à un tracé très approximatif
- Ce même système de guidage risque de faire blocage au crayon dans le tracé de l'ellipse, obligeant à tracer l'ellipse par morceaux, voire d'empêcher tout tracé dans le cas d'ellipses très étroites.
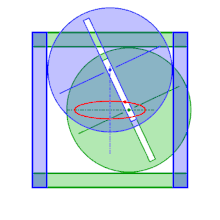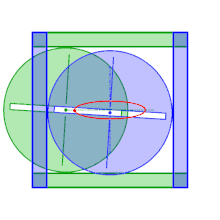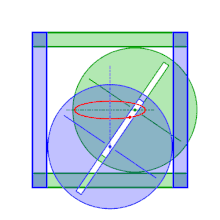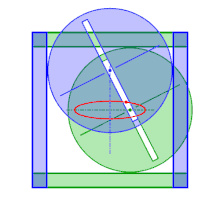
C'est pourquoi se sont construits, sur ce même principe, des ellipsographe où le maintien des point C et D sur les axes se fait de façon indirecte : les points en question deviennent les centres de cercles de même rayon guidés par un cadre extérieur. L'un des cercles est contraint par les deux côtés opposés d'un carré, tandis que l'autre cercle est contraint par les deux autres côtés. Le centre d'un des cercles évolue donc sur une médiane du carré pendant que l'autre évolue sur l'autre médiane. Les deux cercles partagent un même diamètre (rainuré) et sont fixés par des écrous pour que la distance entre les centres soit constante. Ainsi pour tracer une ellipse de demi-grands axes a et b (inférieurs au demi-côté du cadre), il suffit de placer le traceur à une distance du centre d'un des cercles de a, le second cercle est placé et fixé de telle sorte que la distance de son centre au traceur soit égale à b.
C'est sur ce modèle que sont construits l'elliptographe de Farey[6], l'Ellipsenzirkel de Karl Rohn (en)[7] et le HAFF-Ellipsograph[8].
Une autre technique pour fixer la position des points sur les axes du repère consiste à utiliser le théorème de La Hire (ou couple d'al-Tusi) en faisant rouler un cercle de rayon R à l'intérieur d'un cercle de rayon 2R. Alors tout point lié au petit cercle décrit une ellipse. Un tel modèle est exposé au musée des sciences et techniques de Munich.
Ellipsographes de van Schooten
Frans van Schooten, mathématicien néerlandais du XVIIe siècle consacre tout un livre à la construction des sections coniques, De Organica Conicarum Sectionum (1646). Il y reprend le principe exposé par Proclus pour le généraliser à tout point de la droite et en propose un système articulé. Il propose également deux autres mécanismes sous forme d'un antiparallélogramme et d'un losange.
Mécanisme d'Archimède
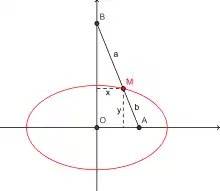
Le principe complète celui d'Archimède : si on considère un segment [AB] de longueur a+b et un point M sur le segment [AB] tels que AM=b, le lieu des points M quand les points A et B se déplacent respectivement sur deux droites perpendiculaires est une ellipse de demi-axes a et b.
En effet, si le point M a pour coordonnées (x,y), le théorème de Pythagore assure que
Soit encore
Or, d'après le théorème de Thalès,
Donc
C'est l'équation caractéristique de l'ellipse de centre O et de demi-axes a et b. Cela assure que le point M est bien sur cette ellipse.
Réciproque, si M est un point de l'ellipse, si on appelle B le point situé sur l'axe des ordonnées, dans le même quadrant que M, et tel que BM=a, et si A est le point d'intersection de (BM) et l'axe des abscisses, on montre aisément, par un raisonnement analogue au précédent que MA=b
L'ellipsographe de van Schooten[9] simplifie le processus en considérant un système articulé OIA dans lequel
. Le point O est fixe, le point A se déplace sur une droite et entraîne les points I et M[3].
Ellipsographe à antiparallélogramme
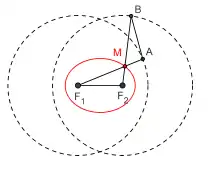
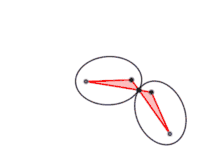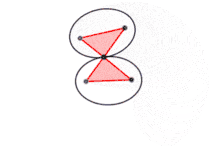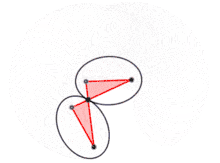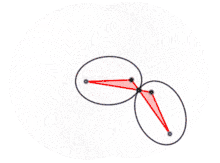
Cet ellipsographe, le second présenté par van Schooten[10], utilise un polygone articulé. Il s'agit d'un antiparallélogramme, c'est-à-dire un quadrilatère croisé F1ABF2 dont les côtés sont égaux deux à deux. Pour tracer l'ellipse de grand axe 2a et dont la distance entre les foyers est 2c, il suffit de prendre
On fixe les sommets F1 et F2 aux foyers de l'ellipse. Quand la branche F1A pivote autour de F1, la branche BF2 pivote autour de F2 et l'antiparallélogramme se déforme. Le point d'intersection M des deux branches parcourt alors l'ellipse recherchée. En effet, les propriétés de symétrie de l'antiparallélogramme assurent que
Or
donc
Ceci est la définition bifocale de l'ellipse, utilisée aussi dans la méthode du jardinier.
Ellipsographe à cercle directeur
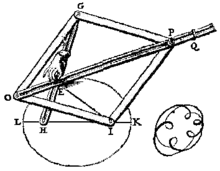
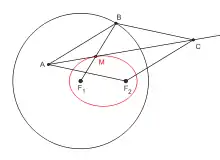
Cet ellipsographe utilise un losange articulé de taille quelconque ABCF2, muni d'une tige coulissante [AC) et d'une barre F1B de longueur 2a. Les points F1 et F2 sont fixés sur les foyers de l'ellipse que l'on cherche à tracer et la barre F1B pivote autour de F1 entraîne le losange qui se déforme. Les barres F1B et AC se rencontrent en M qui décrit l'ellipse de foyers F1 et F2 et de grand axe 2a.
En effet ce mécanisme permet de déterminer, pour chaque position de B sur le cercle directeur de l'ellipse, le centre du cercle passant par F2 et tangent au cercle directeur en B : ce centre se situe sur la médiatrice de [BF2] qui se trouve être la diagonale (AC), et sur le segment F1B. Le centre de ce cercle est bien le point M. Or on sait que l'ensemble de ces centres dessine l'ellipse recherchée (voir construction de l'ellipse par un cercle directeur).
Cet outil permet de plus de préciser en chaque point la position de la tangente à l'ellipse matérialisée ici par la droite (AC). En effet, la propriété de réflexivité de l'ellipse assure que la tangente est la bissectrice extérieure de l'angle F1MF2. Or la droite (AC), axe de symétrie du losange, est la bissectrice de l'angle BMF2 donc bissectrice extérieure de l'angle F1MF2.
Van Schooten montre comment cet instrument peut être utilisé pour le tracé des ellipses[11], mais aussi pour celui des hyperboles[12] et des paraboles[13].
Ellipsographe de Delaunay
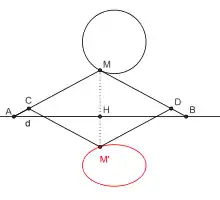
L'ellipsographe de Delaunay, décrit par Nikolai Delaunay (ru) en 1895[14], utilise un système articulé permettant de construire l'image d'une figure par une affinité, ou bien, ce qui est équivalent, l'image d'une figure par projection d'un plan dans un autre plan.
Dans la figure ci-contre les points A et B coulissent sur la droite (d). Les bras MA et MB ont même longueur et CMDM' est un losange articulé. Le point M' est alors l'image du point M dans l'affinité orthogonale d'axe (d) et de rapport
En effet, la droite (MM') coupe l'axe (d) orthogonalement en H et la présence de triangles semblables permet d'établir l'égalité de rapports suivante :
Soit encore
L'ellipse de demi-axes a et b étant l'image d'un cercle de rayon a par une affinité de rapport b/a, elle peut être construite par l'ellipsographe à condition que : lorsque le point M parcourt le cercle de rayon a, son image M' parcourt l'ellipse recherchée.
Ellipsographe de Kopp
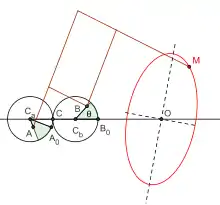
Cet ellipsographe de facture récente, breveté par Franz Otto Kopp en 1993[15], permet de dessiner mais aussi découper des ellipses[16]. Il est constitué de deux roues dentées de même rayon et d'un pantographe. Deux des points du pantographe (A et B) sont fixés sur les roues dentés, en des points légèrement excentrés. Le troisième point (M) dessine alors une ellipse quand une des roues dentées tourne, entraînant sa voisine.
La mise en évidence mathématique de cette propriété peut se faire aisément en utilisant la représentation paramétrique complexe de l'ellipse. Dans le repère de centre C et d'axe (d)=(CCb), les affixes des points A et B peuvent s'exprimer à l'aide de l'angle θ, des distances et , du rayon r des deux roues et du déphasage α entre les deux roues
Selon le principe du pantographe, il existe une constante k telle que AM=kAB, donc l'affixe de M est alors déterminée par
Si l'on se place maintenant dans le repère de centre O d'affixe (2k-1)r (c'est l'image du centre Cb dans l'homothétie de centre Ca et de rapport k) et d'axe (d') faisant avec (d) un angle α/2, le point M a pour affixe
qui est l'équation paramétrique de l'ellipse de centre O, d'axe (d') et de demi-axes
Pour tracer l'ellipse de demi-axes a et b il suffit de placer A et B tels que[17]
Ellipsographes multifonctionnels
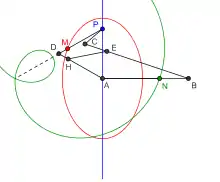
Quand A et B sont fixés, P décrit un segment et M une ellipse.
Quand D et P sont fixés, N décrit une portion de limaçon de Pascal
Les mathématiciens ont également cherché des instruments permettant de tracer de nombreuses courbes en sus des ellipses. Ainsi, en 1818, le mécanicien Joseph Clement reçoit la médaille d'or de la Royal Society of Arts[18] pour la construction d'un appareil qui, non seulement construit des ellipses utilisant un mécanisme analogue à celui d' Archimède ou de Van Schooten[19], mais aussi des cercles, des parallèles, des spirales, et les découpe en sections régulières[20].
Dans le cas de polygones articulés, ils ont cherché à diminuer le nombre de branches tout en augmentant le nombre de fonctionnalités. On peut à ce sujet citer l'ellipsographe décrit en 1879 par Gaston Darboux et construit par Breguet[21], s'inspirant d'un traceur de droite de Harry Hart[22]. Il s'agit d'un pentagone articulé avec contrainte permettant de tracer des perpendiculaires, des ellipses et des limaçons de Pascal[21].
Ellipse passant par 5 points
Il suffit de cinq points pour déterminer une conique. L'application du théorème de Pascal fournit une méthode pour construire la conique en question. Il énonce que, pour tout hexagone dont les sommets sont sur la conique, les points d'intersection des côtés opposés[23] sont alignés:
- Les 5 points connus de la conique permettent de construire un chemin polygonal formé des segments a1, a2, a3, a4;
- Les droites portant a1 et a4 se coupent en I;
- Un 6e point M de la conique permettrait de continuer la ligne polygonale par le segment a5 qui doit rencontrer a2 en un point J que l'on choisit arbitrairement sur la droite portant a2;
- Le segment a6 qui ferme la ligne polygonale doit rencontrer a3 en un point K aligné avec I et J. Le point K est donc à l'intersection de (IJ) et de la droite portant a3;
- le point M correspondant à J est au point de rencontre des droites A1K et A5J.
Ce principe peut être mis en œuvre dans un système articulé formé de 2 bras fixes et 3 bras coulissants et pivotants:
- On place des ventouses sur les 5 points de la conique déjà présents ainsi que sur le point I;
- Les deux bras fixes suivent les segments a2 et a3;
- deux des bras mobiles se rencontrent en J, point mobile sur le bras fixe portant a2, l'un des bras passe par I et l'autre par A5;
- Le bras passant par I rencontre le bras fixe portant a3 en K;
- On place en K un système coulissant et on insère dedans un bras qui va pivoter autour de A1;
- les bras passant par A1 et A5 se rencontrent en M où on place un traceur qui va parcourir l'ellipse.
On rencontre un système analogue, dans le cas où, parmi les cinq points définissant l'ellipse, il y a deux points doubles, dans un modèle de Friedrich Schilling (en)[24], exposé dans la collection des modèles et instruments mathématiques de l'université de Göttingen[25].
Compas à conique
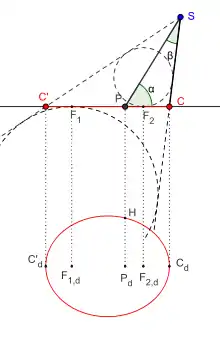
On peut également tracer une ellipse à l'aide d'un compas à conique. C'est un compas dont le bras SP comportant la pointe sèche P est de longueur constante d, le second bras SC est de longueur variable et est conçu pour que le point C reste toujours en contact avec le plan de traçage. L'axe SP conserve une direction constante : il est dans le plan perpendiculaire au plan de traçage et contenant l'axe focal de l'ellipse et conserve un angle constant α avec l'axe focal[26]. Les deux branches conservent un écartement fixe noté β. Lorsque la branche SC tourne autour de l'axe SP, la pointe C dessine dans le plan de traçage une ellipse qui représente l'intersection du cône d'axe SP et d'angle β avec le plan de traçage.
Il est relativement simple de déterminer les caractéristiques de l'ellipse tracée en fonction de d et des angles α et β. Les foyers sont constructibles géométriquement grâce au théorème de Dandelin. Il est en revanche plus complexe d'utiliser le compas à conique pour tracer une ellipse dont les caractéristiques sont fixées. On peut déterminer les angles α et β du compas en fonction de la longueur d du bras SP, du demi-axe a et du paramètre p (demi latus rectum) de l'ellipse[27].
La pointe P doit alors se placer à une distance du centre O de l'ellipse vérifiant
Les premiers compas à coniques, appelés compas parfaits, sont étudiés dès le Xe siècle par les mathématiciens de langue arabe Abū Sahl al-Qūhī, Al-Sijzi (première construction avérée), Ibn al-Haytham, Al-Biruni[28]...
Ceux-ci se sont également préoccupés de trouver comment placer la branche SP du compas pour tracer une ellipse donnée et définissent cette position à l'aide de deux contraintes concernant les points d'intersection de la perpendiculaire à SP passant par S avec l'axe focal (point X) et avec le plan médiateur de l'axe focal (point Y) : les sommets principaux de l'ellipse C et C' et les points S et Y doivent être cocycliques et le rapport XS/XY doit être égal à p/a[29].
Les premiers compas à coniques apparaissent en Europe au cours de la Renaissance (Albrecht Dürer, Léonard de Vinci)[30] au moment où se développe le dessin en perspective[31]. La recherche d'une paternité pour cette découverte est rendue difficile par la multiplicité des versions et la difficulté à déterminer leur filiation. Il semble toutefois que l'un des précurseurs dans l'utilisation d'un tel outil soit le mathématicien, architecte et orfèvre Lorenzo della Volpaia (1446-1512)[32]. S'agit-il d'une découverte indépendante ou bien de la relecture des mathématiciens de langue arabe en particulier concernant les astrolabes ? Les historiens sont partagés sur cette question. Les mêmes doutes apparaissent concernant leur usage : on ne sait pas si le tracé s'appuyait sur des formules mathématiques solides ou une construction géométrique rigoureuse, ou bien si son usage se faisait de manière empirique par ajustements successifs (redresser le compas ou rapprocher la pointe P du sommet principal le plus proche permet de réduire l'excentricité, ouvrir le compas agrandit l'ellipse)[27].
L'intérêt du compas par rapport au système articulé est qu'il permet de tracer des ellipses dont les paramètres peuvent varier continûment[1].
Notes et références
- Raynaud 2007, p. 8.
- Rouse Ball 1909, p. 275.
- Raynaud 2007, p. 9.
- van Schooten 1646, p. 35/55.
- Gaston Tissandier, Nouvelles recettes utiles et appareils pratiques, Masson, 1896, p 95.
- James Smith, The Mechanic or Compendium of pratical Inventions, Henry Fisher, , p. 52-IA1
- (de) Martin Schilling, Catalog mathematischer Modelle : für den höheren mathematischen Unterricht, Leipzig, Martin Schilling, (lire en ligne), Série XXXII p.88 (104) pour la description et le principe et p. 152 (166) pour l'illustration
- (en) « Miscellaneous Instruments », sur Mathematical Instruments, a private collection
- van Schooten 1646, p. 33/53.
- van Schooten 1646, p. 49;50/69;70.
- van Schooten 1646, p. 52/72.
- van Schooten 1646, p. 62/82.
- van Schooten 1646, p. 76/96.
- Delaunay 1895, p. 240.
- (de) Franz Otto Kopp, « Rotational Driven Gear », Brevet, (lire en ligne
 ), n° de patente :4343633A1.
), n° de patente :4343633A1. - Johannes Volmer, Gerhard Ehrlich, David Springett, Ovalturning, p.9.
- Voir E. W. Newton & J. Volmer, Elliptical Turning Association - An Ellipsograph, avec l=k - 1.
- Clement 1818, p. 133.
- Clement 1818, p. 177.
- Clement 1818, p. 134.
- Darboux 1879, p. 7-149.
- Darboux 1879, p. 2-144.
- Plus exactement, les points d'intersection - au sens projectif du terme - des droites portant les côtés opposés
- Schilling 1911, p.67 (83) pour la description et p.152 (166) pour l'illustration.
- « Model362 - Generation of a ellipse by Pascal's theorem », sur Göttingen Collection of mathematical models and instruments
- Pour une réalisation pratique voir, par exemple Le compas parfait présenté sur le site Macchinematematiche.org.
- Raynaud 2007, p. 16.
- Raynaud 2007, p. 27-28.
- Raynaud 2007, p. 17.
- Raynaud 2007, p. 21.
- Raynaud 2007, p. 39.
- Raynaud 2007, p. 23-24.
Bibliographie
- Dominique Raynaud, « Le tracé continu des sections coniques à le Renaissance : applications optico-perspectives, héritage de la tradition mathématique arabe », Arabic Sciences and Philosophy, no 17, , p. 239-345 (lire en ligne)
- N. Delaunay, « Sur quelques nouveaux mécanismes : projecteur, ellipsographe, ellipsoïdographe et hyperbolographe », Bulletin des sciences mathématiques, vol. 19, no 2, , p. 240-245 (lire en ligne)
- Gaston Darboux, « Sur un nouvel appareil à ligne droite de M. Hart », Bulletin des sciences mathématiques et astronomiques, vol. 3, no 1, , p. 144-155 (lire en ligne)
- (en) Joseph Clement, « Instrument for describing ellipses », Transactions of The Society Instituted at London for the Encouragement of Arts, Manufactures and Commerce, vol. 35-36, , p. 133-177
- W. W. Rouse Ball, Récréations mathématiques et problèmes des temps anciens et modernes, Hermann, (lire en ligne)
- (la) Frans van Schooten, De Organica Conicarum Sectionum In Plano Descriptione, Tractatus. Geometris, Opticis; Præsertim verò Gnomonicis et Mechanicis Utilis. Cui subnexa est Appendix, de Cubicarum Æquationum resolutione, (lire en ligne)
Liens externes
- (it) Coniche e conicografi sur le site Associazione macchine matematiche
- Animations sur divers ellipsographes sur le site Mélusine
- Animation d'ellipsographe et fichier Maple sur le site d'Alain Esculier
- Portail de la géométrie