Vecteur

Les bipoints (A, B), (C, D), (E, F) sont équipollents. Ils constituent trois représentants d'un même vecteur. En effet, les quadruplets de points ABFE et ABDC définissent deux parallélogrammes.

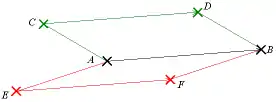
Un vecteur est représenté par un segment orienté (une flèche), ayant pour extrémités un point de départ et un point d'arrivée. L’emplacement dans le plan ou l'espace n’a pas d’importance, deux déplacements de deux points d'origine distincts peuvent correspondre au même vecteur, seuls comptent sa longueur, sa direction et son sens. Il est donc possible de le faire glisser librement dans le plan, parallèlement à lui-même. Si A et B sont deux points distincts, le vecteur ${\displaystyle {\overrightarrow {AB}}}$ possède trois éléments caractéristiques :

• sa direction (droite (AB)) ;
• son sens (il y a deux sens possibles de parcours de la droite (AB) : de A vers B ou de B vers A) ;
• sa norme (ou sa longueur, la longueur du segment [AB]).

Attention cependant à ne pas confondre sens et direction. En effet, dans le langage courant, lorsqu'on se trouve sur une route entre Paris et Versailles et que l'on dit que l'on va dans la direction de Versailles, on se rapproche de cette dernière ville. Mais dans le langage mathématique, la direction est portée par la route (direction Paris-Versailles) sans savoir si l'on va de Versailles vers Paris ou de Paris vers Versailles. Pour savoir vers quelle ville on se dirige, il faudra aussi donner le sens : le sens Paris-Versailles par exemple pour indiquer que l'on va de Paris vers Versailles.

Une définition formelle utilise au préalable la notion de bipoint. Il est défini comme un couple de points. L’ordre a une importance : le premier point est appelé origine. Deux bipoints (A, B) et (C, D) sont dits équipollents lorsque les segments [AD] et [BC] ont le même milieu. La relation d'équipollence constitue une relation d'équivalence sur les bipoints. Une classe d'équivalence contient tous les bipoints dont le deuxième membre est l'image du premier point par le déplacement.

La classe d'équivalence d'un bipoint (A, B) est appelée vecteur et est notée ${\displaystyle {\overrightarrow {AB}}}$. Le bipoint (A, B) en est un représentant. Réciproquement, tout vecteur admet plusieurs bipoints représentants, dont aucun n'est privilégié. Si une origine est choisie, il existe un unique bipoint représentant un vecteur donné.

Si les vecteurs peuvent être déplacés dans le plan, quant à eux, les points ne le sont pas. Ces derniers restent fixes. L'intérêt d'avoir un représentant d'un vecteur est d'obtenir, parmi les bipoints équipollents, un seul dont l'origine ou l'extrémité est fixée une fois pour toutes.

Ainsi deux bipoints (A, B) et (C, D) sont équipollents si et seulement s'ils représentent le même vecteur et on peut alors écrire l'égalité

${\displaystyle {\overrightarrow {AB}}={\overrightarrow {CD}}.}$

Tous les bipoints constitués de la répétition d'un même point : (A, A), sont équipollents entre eux, ils sont les représentants d'un vecteur qualifié de nul. Il est noté

${\displaystyle {\overrightarrow {AA}}={\overrightarrow {0}}}$.

Cet unique vecteur possède la propriété particulière d'avoir son origine et son extrémité confondues. Ce vecteur sera alors le seul à être représenté comme un point. Un vecteur représente un déplacement. Mais dans un vecteur nul, l'extrémité et l'origine étant confondues, il n'y a aucun déplacement. Cela veut donc dire que l'absence de déplacement est considérée comme un déplacement.

Les théories présentant les vecteurs comme une classe d'équivalence de bipoints les notent en général par une lettre surmontée d'une flèche[1].

La longueur d'un bipoint (A, B) est définie comme la longueur du segment sous-jacent. Deux bipoints équipollents ont la même longueur. Tous les représentants d'un vecteur ${\displaystyle {\vec {u}}}$ ont donc la même longueur, qui est appelée norme (ou module) du vecteur ${\displaystyle {\vec {u}}}$, et notée en général ${\displaystyle ||{\vec {u}}||}$ (on utilise aussi parfois simplement la ou les lettres désignant le vecteur sans la flèche, par exemple u ou AB). Un vecteur unitaire est un vecteur de norme 1. Le vecteur nul est de norme nulle, ${\displaystyle ||{\vec {0}}||=0}$.

L’angle que forment deux vecteurs ${\displaystyle {\vec {u}}}$ et ${\displaystyle {\vec {v}}}$ est noté ${\displaystyle ({\widehat {{\vec {u}},{\vec {v}}}})}$. Il est défini comme l'angle que font deux représentants de même origine. Ainsi si (A, B) est un représentant de ${\displaystyle {\vec {u}}}$ et (A, C) un représentant de ${\displaystyle {\vec {v}}}$, alors

${\displaystyle ({\widehat {{\vec {u}},{\vec {v}}}})={\widehat {BAC}}}$

Dans le plan orienté, il est possible de définir la notion d'angle orienté de deux vecteurs. Ce n'est pas le cas dans l'espace.

Des constructions géométriques permettent la définition de l'addition et de la multiplication par un scalaire. Le nom donné aux opérations est la conséquence de la similarité avec les opérations sur les nombres (commutativité, associativité et distributivité, présence d'un élément neutre et absorbant). Pour cette raison, non seulement les noms des opérations mais les notations sont similaires.

Si ${\displaystyle {\vec {u}}}$ et ${\displaystyle {\vec {v}}}$ sont deux vecteurs, soit un couple (A, B) de points représentant ${\displaystyle {\vec {u}}}$ et C le point tel que le couple (B, C) représente le vecteur ${\displaystyle {\vec {v}}}$. Alors un représentant du vecteur ${\displaystyle {\vec {u}}+{\vec {v}}}$ est le couple (A, C). Si ${\displaystyle {\vec {v}}}$ est le vecteur nul, alors les points B et C sont confondus, la somme est alors égale à ${\displaystyle {\vec {u}}}$ et le vecteur nul est bien l'élément neutre pour l'addition des vecteurs. Soit α un nombre, si ${\displaystyle {\vec {u}}}$ est le vecteur nul, alors ${\displaystyle \alpha {\vec {u}}}$ est aussi le vecteur nul, sinon il existe une unique droite contenant A et B, et un unique point C tels que la distance entre A et C soit égale à ${\displaystyle |\alpha |\;\cdot ||{\vec {u}}||}$ et le sens de (A, B) si α est positif, relativement au sens de ${\displaystyle {\vec {u}}}$, et l'inverse sinon.

Une fois équipée d'une structure d'espace vectoriel, les démonstrations de la géométrie euclidienne s’avèrent souvent simplifiées. Un exemple est donné par le théorème de Thalès.

David Hilbert propose une construction axiomatique de la géométrie euclidienne rigoureuse.

On ne trouve pas de vecteurs dans les Éléments d'Euclide, mais les notions de point ou de parallélogramme, de l'approche esquissée ci-dessus y sont bien présentes. Mais l'axiomatisation des Éléments n'est pas tout à fait satisfaisante, bien qu'elle ait été longtemps un modèle en la matière : certains axiomes restent implicites. David Hilbert a montré comment axiomatiser rigoureusement le plan ou l'espace affine de façon géométrique (voir les articles plan affine de Desargues et axiomes de Hilbert). En utilisant le parallélisme, il est alors possible de définir les translations et les homothéties, et en utilisant ces transformations, les vecteurs et les scalaires[2]. Cette approche est très générale : elle permet de traiter des cas utiles, où les scalaires ne sont pas forcément des réels, mais par exemple des complexes ou les éléments d'un ensemble fini de nombres[2]. Elle se généralise également en dimension quelconque, au moins finie[2].

Cependant le développement des mathématiques a élargi considérablement les domaines d'utilisation des vecteurs, et une approche plus algébrique est très largement utilisée. Elle est fondée sur deux ensembles : l'un contenant les scalaires, l'autre les vecteurs. Le deuxième est appelé espace vectoriel. Ces deux ensembles sont munis d'opérations et des axiomes sont vérifiés pour chacune des opérations. Cette construction différente pour formaliser le même concept de vecteur est celle qui est traitée dans l'article consacré aux espaces vectoriels. Elle est esquissée ci-dessous.

Dans un plan, deux vecteurs ${\displaystyle {\vec {a}}}$ et ${\displaystyle {\vec {b}}}$ non nuls et de directions différentes possèdent une propriété importante. Un vecteur ${\displaystyle {\vec {u}}}$ quelconque est somme d'un multiple de ${\displaystyle {\vec {a}}}$ et d'un multiple de ${\displaystyle {\vec {b}}}$. Cela signifie qu'il existe un unique couple de nombres, (u₁, u₂), tel que

${\displaystyle {\vec {u}}=u_{1}{\vec {a}}+u_{2}{\vec {b}}}$.

${\displaystyle {\vec {u}}}$ est alors qualifié de combinaison linéaire de ${\displaystyle {\vec {a}}}$ et ${\displaystyle {\vec {b}}}$. Comme tout vecteur du plan s'exprime de manière unique comme combinaison linéaire de ${\displaystyle {\vec {a}}}$ et ${\displaystyle {\vec {b}}}$, la famille ${\displaystyle ({\vec {a}},{\vec {b}})}$ est qualifiée de base du plan et u₁, u₂ sont appelés composantes[3] du vecteur ${\displaystyle {\vec {u}}}$ dans cette base. Cette définition correspond à celle d'un plan affine muni d'un repère. Une telle propriété est encore vraie dans l'espace. Cependant, deux vecteurs ne suffisent plus, toute base contient exactement trois vecteurs non nuls et dont les directions ne sont pas coplanaires (c'est-à-dire qu'il n'existe aucun plan contenant les trois directions). Si dans l'espace, les trois composantes d'un vecteur ${\displaystyle {\vec {u}}}$ sont u₁, u₂ et u₃, il est d'usage de noter :

${\displaystyle {\vec {u}}={\begin{pmatrix}u_{1}\\u_{2}\\u_{3}\end{pmatrix}}}$

pour indiquer les composantes du vecteur. Le tableau est appelé vecteur colonne et correspond à un cas particulier de matrice. Les opérations algébriques sur les vecteurs sont simples, avec une telle représentation. Additionner deux vecteurs revient à additionner chacune des composantes et la multiplication par un scalaire revient à multiplier chaque composante par le scalaire.

Dans un plan vectoriel, un vecteur s'identifie à un couple de scalaires, et dans l'espace à un triplet. Si les nombres choisis sont réels alors un plan (respectivement un espace) s'identifie à ℝ² (respectivement à ℝ³). Ici, ℝ désigne l'ensemble des nombres réels.

La logique précédente, appliquée pour une dimension égale à deux ou trois se généralise. Il est ainsi possible de considérer la structure ℝⁿ ou de manière plus générale Kⁿ avec K un ensemble de scalaires possédant de bonnes propriétés (précisément, K est un corps commutatif). Une telle structure possède une addition, et une multiplication par un scalaire définies comme au paragraphe précédent.

Il est possible de généraliser encore la définition d'un vecteur. Si un ensemble E possède une addition et une multiplication scalaire sur un corps commutatif et si ses opérations vérifient certaines propriétés, appelées axiomes et décrites dans l'article détaillé, alors E est appelé espace vectoriel et un élément de E vecteur.

De très nombreux exemples d'ensembles mathématiquement intéressants possèdent une telle structure. C’est le cas par exemple des espaces de polynômes, de fonctions vérifiant certaines propriétés de régularité, de matrices... Tous ces ensembles peuvent alors être étudiés avec les outils du calcul vectoriel et de l'algèbre linéaire.

La notion de dimension fournit le premier résultat de classification concernant les espaces vectoriels. Dans un espace vectoriel de dimension finie n, il est possible, moyennant le choix d'une base, de se ramener au calcul sur des vecteurs colonnes de taille n. Il existe également des espaces vectoriels de dimension infinie. L'ensemble des fonctions de ℝ dans ℝ est ainsi un espace vectoriel sur le corps des nombres réels, de dimension infinie. Vue sous cet angle, une telle fonction est un vecteur.

Si les deux constructions, algébrique et géométrique, sont équivalentes pour les structures vectorielles du plan et de l'espace usuel, la géométrie apporte en plus les notions de distance et d'angle.

La notion de produit scalaire permet de combler cette lacune. Un produit scalaire associe à deux vecteurs un réel. Si les deux vecteurs sont identiques le réel est positif. Il existe un produit scalaire tel que la norme du vecteur soit égale à la racine carrée du produit scalaire du vecteur avec lui-même. La géométrie euclidienne apparaît alors comme l'étude d'un espace affine comprenant un espace vectoriel de dimension deux ou trois sur le corps des réels, muni d'un produit scalaire : plan affine euclidien ou espace affine euclidien.

Une fois équipée d'un produit scalaire, il devient possible de définir sur l'espace vectoriel des transformations classiques de géométrie euclidienne comme la symétrie, la rotation ou la projection orthogonale. La transformation associée aux espaces vectoriels laisse toujours invariant le vecteur nul. Les rotations permettent de définir la notion d'angle pour les vecteurs. L'angle ${\displaystyle \scriptstyle ({\widehat {{\vec {u}},{\vec {v}}}})}$ est égal à ${\displaystyle \scriptstyle ({\widehat {{\vec {u'}},{\vec {v'}}}})}$ si et seulement s'il existe une rotation qui envoie ${\displaystyle \scriptstyle {\vec {u}}}$ sur ${\displaystyle \scriptstyle {\vec {u'}}}$ et ${\displaystyle \scriptstyle {\vec {v}}}$ sur ${\displaystyle \scriptstyle {\vec {v'}}}$. Cette définition, qui s'applique à une formalisation algébrique de la notion d'espace vectoriel, est équivalente à celle de la construction géométrique. Une telle approche simplifie parfois grandement les démonstrations, un exemple est le théorème de Pythagore.

L'approche algébrique permet de définir toutes les notions de la géométrie euclidienne, elle généralise cette géométrie à une dimension quelconque si les nombres sont réels. Dans le cas des nombres complexes une construction analogue, appelée espace hermitien, existe.

En effectuant le produit scalaire d'un vecteur ${\displaystyle x=x^{i}e_{i}}$ par le vecteur de base ${\displaystyle e_{j}}$, on obtient la composante covariante de ce vecteur

${\displaystyle x.e_{j}=(x^{i}e_{i}).e_{j}=x^{i}(e_{i}.e_{j})=x^{i}.g_{ij}=x_{j}}$

avec ${\displaystyle g_{ij}=e_{i}.e_{j}}$ , le tenseur métrique égal au produit scalaire des vecteurs de base (valant ${\displaystyle \delta _{ij}}$ lorsque la base est orthonormée).

Les composantes contravariantes sont les composantes du vecteur telles que ${\displaystyle x=x^{i}e_{i}}$

On note les composantes contravariantes par un indice supérieur, les composantes covariantes par un indice inférieur.

En multipliant les composantes contravariantes par le tenseur métrique, on obtient les composantes covariantes

${\displaystyle x^{i}g_{ij}=x_{j}}$

Dans un système orthonormé les composantes covariantes et contravariantes sont identiques

Géométriquement pour un système quelconque, en projetant un vecteur ${\displaystyle {\overline {OM}}}$ parallèlement aux axes, on obtient deux points M' et M'' dont les coordonnées par rapport aux vecteurs de base définissent les coordonnées contravariantes du vecteur ${\displaystyle {\overline {OM}}=x^{1}e_{1}+x^{2}e_{2}}$.

En projetant le même vecteur ${\displaystyle {\overline {OM}}}$ perpendiculairement, on obtient deux points m' et m'' dont les coordonnées par rapport aux vecteurs de base définissent les coordonnées covariantes du vecteur[4]

Représentation graphique d'un point dans le plan complexe. Les coordonnées cartésiennes correspondent à celle d'un point dans le repère d'origine 0 et de base les nombres 1 et i.

Une vaste partie des mathématiques utilise les vecteurs, en algèbre, en géométrie ou en analyse.

Un exemple archétypal en algèbre est la résolution d'un système d'équations linéaires. Un exemple de trois équations à trois inconnues correspond à la recherche des vecteurs de dimension trois, antécédents d'une application linéaire d'un vecteur donné. Le plan euclidien ℝ² peut aussi être identifié au plan complexe ℂ. La base canonique est composée de deux vecteurs unitaires : l'unité des réels et l'unité imaginaire.

Les vecteurs offrent un outil efficace pour la résolution de nombreux problèmes de géométrie. Ils sont utilisés pour la détermination de propriétés de parallélisme ou d'orthogonalité de droites, plan ou segments. À travers l'utilisation des coordonnées barycentriques, les vecteurs forment un outil adapté pour caractériser le centre d'une figure géométrique et permettent une démonstration simple du théorème de Leibniz, du théorème de Ceva comme de nombreux résultats sur la géométrie du triangles. Le produit scalaire, qui s'exprime particulièrement simplement dans une base orthonormée, offre de nombreuses possibilités. Il permet, par exemple, de mesurer la distance d'un point à une droite ou à un plan. Une telle base permet d'exprimer aussi simplement des transformations géométriques comme la projection orthogonale sur un plan ou une droite.

L'analyse n'est pas en reste. L'espace vectoriel ℝ², copie du plan euclidien est le cadre naturel de représentation du graphe d'une fonction. Les vecteurs permettent par exemple de déterminer la droite perpendiculaire à une courbe en vue de déterminer les foyers d'une conique. La représentation graphique offre une solution pour déterminer une approximation d'une racine d'une équation dans le cas où une résolution par une méthode algébrique n'est pas connue[5].

La trajectoire des planètes se modélise dans un langage vectoriel. Les travaux d'Isaac Newton sur cette question sont à l'origine du mot vecteur.

En présence d'un champ magnétique, des petites boussoles s'orientent, indiquant la direction et le sens des vecteurs du champ.

La physique est à l'origine du terme de vecteur, elle utilise toujours largement ce concept. La raison historique provient du fait qu'en physique classique l'espace qui nous entoure est bien modélisé comme espace affine (géométrie euclidienne) de dimension trois avec le temps (absolu) comme paramètre d'évolution. En physique, une addition de vecteurs ne peut avoir de sens que si leurs coordonnées respectives ont la même dimension.

La position d'un point est décrite par des coordonnées dans un repère, mais sa vitesse et son accélération sont des vecteurs. Pour établir la mécanique du point, c'est-à-dire l'étude des mouvements d'un point matériel, les vecteurs sont indispensables. La position d'un point se modélise par ses trois coordonnées (qui sont des nombres réels) dont chacune est une fonction du temps ; on peut aussi la décrire par le vecteur position allant de l'origine du repère au point : les composantes du vecteur sont alors identifiables aux coordonnées du point. Le vecteur vitesse est égal à la dérivée du vecteur position (c'est-à-dire : les composantes du vecteur vitesse sont les dérivées de celles du vecteur position), et c'est encore un vecteur. Il en est de même pour l'accélération, correspondant à la dérivée seconde.

Dans un référentiel galiléen, l'accélération d'un point est proportionnelle à la force qui lui est appliquée. Une force est équivalente à un vecteur. La trajectoire d'une planète est connue par la force qui lui est appliquée à chaque instant. Cette force est la conséquence de la gravitation, essentiellement due au Soleil. Ce phénomène est décrit par la donnée du champ gravitationnel. Ce champ associe un vecteur proportionnel à la force de la gravitation à chaque point de l'espace.

Cette modélisation s'accommode plus difficilement de la relativité restreinte du fait que les changements de référentiels n'y dépendent pas linéairement de la vitesse, et elle ne concerne pas la relativité générale qui n'utilise pas d'espace euclidien (sauf pour des approximations). En physique quantique les coordonnées ne peuvent être celles d'une particule qu'en tenant compte du principe d'incertitude, et les forces sont dues à des échanges de particules.

Les Éléments formalise une structure géométrique initialement utilisée pour décrire l'ancêtre de l'espace vectoriel.

La civilisation grecque développe la géométrie à un niveau inégalé à cette époque. L'un des fleurons est le traité nommé les Éléments d'Euclide, datant du III^e siècle av. J.-C.. Il contient la formalisation, très rigoureuse pour l'époque, d'une géométrie, encore maintenant appelée euclidienne. On y trouve les définitions d'une droite, d'un plan ou de notre espace physique de dimension trois permettant de modéliser des volumes. Les propriétés des distances, des angles, des mesures de surfaces et de volumes sont étudiées. Les théorèmes fondateurs, comme ceux appelés Thalès ou Pythagore, sont explicités et démontrés.

Les Neuf Chapitres sur l'art mathématique ont en Chine un rôle analogue aux Éléments d'Euclide en occident.

La Chine développe les premières idées algébriques à l'origine des vecteurs^{[réf. nécessaire]}. Un vieux texte, datant probablement du I^er siècle av. J.-C.[7] : les Neuf Chapitres sur l'art mathématique y consacre sa huitième partie. Elle s'intitule Fang cheng ou Disposition rectangulaire et traite d'un problème maintenant appelé système d'équations linéaires. Cette culture n'en reste pas là, Qin Jiushao (1202 - 1261) généralise cette étude à des nombres différents des entiers ou rationnels. Il utilise les congruences, inaugurant une démarche consistant à définir des vecteurs sur des ensembles de nombres exotiques. Il peut ainsi résoudre des problèmes liés au calendrier et aux alignements de planètes avec une très grande précision[8]. La méthode utilisée ne sera connue qu'au XIX^e siècle en Occident, sous le nom de pivot de Gauss. Ce résultat est suffisamment étonnant pour que Ulrich Libbrecht (en) précise que : « Nous ne devrions pas sous-estimer la percée révolutionnaire de Qin, en effet, depuis le théorème des restes chinois de Sun Zi, on passe sans intermédiaire à un algorithme plus avancé que la méthode de Gauss elle-même, et il n'y a pas la moindre indication d'une évolution graduelle[9]. »

L'aspect géométrique n'échappe pas aux mathématiciens chinois. Le dernier chapitre, le Gou gu comporte un équivalent du théorème de Thalès et de Pythagore[10].

Illustration extraite du traité de perspective De prospectiva pingendi de Piero della Francesca, un peintre de la Renaissance italienne.

L'existence d'un lien entre ce que l'on appelle maintenant l'algèbre et la géométrie est ancienne. Les Babyloniens connaissaient déjà la propriété algébrique de la diagonale d'un carré de côté de longueur un, à savoir que son carré est égal à deux. Ils savaient de plus calculer cette valeur avec une remarquable précision[11]. Ce lien est aussi connu des Grecs et des Chinois.

Il faut cependant attendre la civilisation islamique pour observer un progrès significatif. Leurs mathématiciens connaissaient les travaux des Grecs, particulièrement ceux d'Euclide[12]. Les notations utilisées laissent penser qu'ils avaient aussi accès à des travaux des premiers mathématiciens chinois[13]. Le progrès déterminant consiste à associer au plan géométrique des coordonnées. Omar Khayyam (1048 - 1131) cherche les solutions d'un problème purement algébrique : trouver les racines d'un polynôme du troisième degré. Un système de coordonnées lui permet de visualiser ces racines comme les abscisses des intersections d'une parabole et d'une hyperbole[14].

Le système des coordonnées est repris en Europe. La volonté de maîtriser la perspective pousse les peintres italiens à étudier les mathématiques. Filippo Brunelleschi (1377 - 1446) découvre les lois de la perspective, issues d'une projection centrale[15]. Ces résultats sont formalisés[16] par Leon Battista Alberti (1404 - 1472). Les théoriciens de la perspective disposent de multiples talents. Ainsi Piero della Francesca (vers 1412 - 1492), auteur d'un traité sur la question[17], est à la fois peintre et mathématicien. Giorgio Vasari (1511 - 1574) indique, à propos de ses talents de géomètre : « Il ne fut inférieur à personne de son époque et peut-être de tout temps[18] ».

René Descartes utilise l'optique pour développer le concept de repère cartésien. L'illustration provient de son traité : Les Dioptriques.

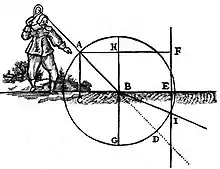
La physique est le moteur suivant de la convergence entre géométrie et algèbre. En 1604, Galileo Galilei (1564 - 1642) établit[19] la loi de la chute des corps. Les illustrations de ses notes montrent l'utilisation d'un repère. L'optique est la branche qui aboutit au progrès le plus marquant. Pierre de Fermat (1601 - 1665), qui connaissait les écrits de Galilée, et René Descartes (1596 - 1650) s'écrivent des lettres au sujet de la dioptrique (la manière dont la lumière se réfléchit sur un miroir) et à la réfraction (la déviation d'un rayon lumineux quand il change de milieu, par exemple en passant de l'air à l'eau)[20]. Ils arrivent à la conclusion qu'un repère est une méthode systématique permettant d'appréhender tous les problèmes de géométrie euclidienne. Ces résultats sont consignés dans un traité de Descartes[21]. Il écrit en introduction : « Comment le calcul d'arithmétique se rapporte aux opérations de géométrie ». Pour Descartes, « calcul d'arithmétique » signifie approximativement ce qui est maintenant appelé « algèbre ». Cette approche est particulièrement féconde pour l'étude d'une branche naissante des mathématiques : la géométrie analytique. Un exemple est donné par l'étude de la cycloïde. Cette courbe décrit la trajectoire d'un point de la surface d'une roue se déplaçant sans glissement sur un sol horizontal.

Isaac Newton (1643 - 1727) développe[22] la géométrie analytique et l'utilise en astronomie. Cette application est l'origine[23] de l'utilisation du terme vecteur. En 1704, un dictionnaire technique anglais indique :

« Une ligne dessinée depuis une planète, se déplaçant autour d'un centre ou du foyer d'une ellipse, jusqu'à ce centre ou ce foyer, est appelé Vecteur par quelques auteurs de la Nouvelle Astronomie, car cette ligne semble porter la planète autour du centre[24]. »

Ce terme apparaît en français sous la plume de Pierre-Simon de Laplace (1749 - 1827) dans l'expression rayon vecteur[25], encore dans un contexte astronomique. Il vient du latin vector provenant lui-même du verbe vehere qui veut dire transporter[26]. Pour les Romains, le mot vector désignait aussi bien le passager que le conducteur d'un bateau ou d’un chariot. Les mots français véhicule, voiture, mais aussi invective proviennent de cette même racine latine. Son origine est plus ancienne, elle provient de l'indo-européen *VAG, ou *VAGH et signifie chariot.

Ainsi, au XVII^e siècle, le contexte géométrique et algébrique du vecteur est présent. En revanche, aucune formalisation n'est proposée et le terme, s'il est utilisé, désigne encore une grandeur scalaire.

Giusto Bellavitis est un mathématicien italien auteur de la formalisation des vecteurs par la notion de bipoint et d'équipollence.

La première formalisation des vecteurs est le fruit d'un travail de plusieurs mathématiciens durant la première moitié du XIX^e siècle. Bernard Bolzano publie un livre élémentaire[27] contenant une construction axiomatique de la géométrie analogue à celle d'Euclide, fondée sur des points, droites et plans. Il adjoint les opérations algébriques d'addition et de multiplication. La géométrie projective, héritière du travail sur la perspective des peintres de la renaissance italienne, conduit Jean-Victor Poncelet et Michel Chasles à affiner[28]^,[29] les travaux de Bolzano. August Ferdinand Möbius apporte sa pierre à l'édifice en développant le système de coordonnées barycentriques[30]. Enfin, la formalisation encore actuellement enseignée, à partir des notions de bipoint et d'équipollence, est l'œuvre[31] de Giusto Bellavitis.

Une autre voie est explorée, purement algébrique. William Rowan Hamilton remarque que les nombres complexes représentent un plan euclidien. Il passe dix ans de sa vie[32] à chercher un équivalent en dimension trois, et finit par trouver le corps des quaternions, de dimension quatre en 1843. Il propose deux nouvelles définitions pour les mots « vecteur » et « scalaire ». Un vecteur est pour lui un élément d'un sous-ensemble des quarternions, de dimension trois. Il écrit :

« Un vecteur est donc […] une sorte de triplet naturel (suggéré par la géométrie) : et en conséquence nous verrons que les quaternions offrent une représentation symbolique simple de tout vecteur sous forme trinomiale (ix + jy + kz) ; ce qui ramène la conception et l'expression d'un tel vecteur à la forme la plus proche possible de celle obtenue avec les coordonnées cartésiennes et rectangulaires[33]. »

En 1878, dans Éléments de dynamique William Kingdon Clifford reprendra en la simplifiant la notion de quaternions. Il introduit en particulier le produit scalaire et le produit vectoriel de deux vecteurs. Cette approche permit d'utiliser les vecteurs d'une manière plus calculatoire.

Cette deuxième voie, qui donne pour la première fois une signification analogue aux formalisations modernes de la notion de vecteur, est ensuite précisée et enrichie. Elle consiste maintenant à définir un vecteur comme un élément d'un espace vectoriel.

Les applications linéaires d'un espace vectoriel dans un autre sont des fonctions respectant l'addition et la multiplication externe. Elles s'additionnent et se multiplient scalairement, et disposent donc des propriétés qui font d'elles des vecteurs. Il en est de même pour les matrices de format fixé, même si elles ne sont pas de type colonne : ces matrices forment toujours un espace vectoriel.

Les deux exemples précédents correspondent à des cas où la structure est enrichie par une multiplication interne. Elle porte le nom d'algèbre, ses éléments sont appelés souvent vecteurs et parfois points. Des exemples sont données par l'ensemble des polynômes à coefficients réels ou encore une algèbre de Lie.

Dans d'autres cas, la structure est appauvrie. Un module est une structure analogue telle que les scalaires différents de zéro ne sont plus toujours inversibles. Le terme de vecteur est néanmoins toujours utilisé.

Selon le point d'application des forces, le solide bascule ou non. L'objet mathématique associé est un vecteur glissant.

Les lois établissant les mouvements d'un point s'appliquent aussi dans le cas d'un solide, les calculs deviennent néanmoins plus complexes^{[pertinence contestée]}. Si les vecteurs restent omniprésents, le point d'application de la force possède son importance. Selon sa position, le solide tourne en plus du déplacement de son centre de gravité. Pour tenir compte de ce phénomène, de nouvelles définitions sont proposées. Un vecteur lié ou pointeur est un couple composé d'un vecteur et d'un point appelé point d'application. La rotation du solide est la conséquence d'une grandeur physique appelé moment. Elle ne dépend pas de la position du vecteur sur une droite donnée. Pour cette raison, un vecteur glissant est un couple composé d'un vecteur et d'une droite affine. Dans ce contexte, et pour éviter toute ambigüité, un vecteur au sens classique du terme est appelé vecteur libre[34].

Pour tenir compte à la fois de la rotation et du mouvement du centre de gravité, un être mathématique plus complexe est utilisé. Il porte le nom de torseur[35]. Il correspond à un vecteur de dimension six, trois composantes décrivent le déplacement du centre de gravité et les trois autres la rotation du solide. Les torseurs possèdent en plus une loi de composition spécifique. La physique utilise d'autres généralisations, on peut citer le tenseur ou le pseudovecteur.

Image vectorielle	Image matricielle

L'informatique utilise le terme de vecteur, à la fois pour des raisons géométriques et algébriques. Le codage d'une image sur un écran d'ordinateur utilise au choix deux techniques : matricielle et vectorielle. La première utilise des éléments graphiques définis point par point. À chaque pixel est associée la quantité de couleurs primaires correspondante. Si cette méthode est économique en matière de puissance de calcul, un agrandissement de la taille de l'image possède pour conséquence un effet d'escalier.

Un dessin vectoriel est une représentation composée d'objets géométriques (lignes, points, polygones, courbes…) ayant des attributs de forme, de position, de couleur, etc. À la différence de la technique précédente, il s'agit d'une méthode plus coûteuse en matière de puissance de calcul mais dans laquelle l'effet d'escalier n'existe pas[36].

La représentation des données en informatique, pour les fonctions de mémoire ou de calcul, se fonde sur des tableaux d'octets. Si un octet est identifié à un scalaire, ce qui se conçoit car deux octets s'additionnent et se multiplient, alors un tel tableau s'apparente à une famille de composantes vectorielles. Pour cette raison, un tel tableau est appelé vecteur. Par extension, le terme de vecteur désigne aussi des tableaux dont les composantes sont autre chose que des nombres, par exemple des pointeurs ou des structures informatiques quelconques[37].

En linguistique, les vecteurs sont utilisés pour quantifier le degré de similarité sémantique entre plusieurs mots. La proximité sémantique entre plusieurs mots est d'autant plus forte que la proximité spatiale entre vecteurs est élevée. Calculée à partir d'un indice compris entre 0 et 1 (0 = proximité nulle, 1 = proximité maximale), elle est obtenue à partir de l'angle ou de la longueur. La polysémie constitue une limite de cette approche : ainsi, le mot "vol" désigne à la fois un larcin et un déplacement dans l'air (et sera donc proche de mots en rapport avec l'une ou l'autre signification, ce qui rapprochera des mots sans rapport entre eux), ce qui peut se résoudre en prenant en compte le contexte linguistique[38]. Un autre facteur de pertinence de la représentation vectorielle est la fréquence du mot : moins le mot est employé et moins la représentation vectorielle sera pertinente, d'où une proposition de fixer un seuil de fréquence minimale[39] ^, [40].

• (en) Premières utilisations connues des termes mathématiques par J. Miller
• (en) John J. O'Connor et Edmund F. Robertson, « Abstract linear spaces », dans MacTutor History of Mathematics archive, université de St Andrews (lire en ligne).

• (en) Michael J. Crowe, A History of Vector Analysis: The Evolution of the Idea of a Vectorial System, Dover Publications Inc., 28 mars 2003 (ISBN 978-0-486-67910-5)
• (en) Jean-Luc Dorier, « A general outline of the genesis of vector space theory », Historia mathematica, vol. 22, n^o 3,‎ 1995, p. 227–261 (ISSN 0315-0860, DOI 10.1006/hmat.1995.1024, lire en ligne, consulté le 3 février 2021)
• (en) J. V. Field, The Invention of Infinity: Mathematics and Art in the Renaissance, Oxford University Press, 1997 (ISBN 0198523947)
  Ce texte montre comment les artistes de la Renaissance produisent des mathématiques qui non seulement révolutionnent leur métier, mais contribuent aussi aux mathématiques pures.

• F. Casiro, A. Deledicq, Pythagore et Thalès Les éditions du Kangourou 1998 (ISBN 2-87694-040-X)
  Ce texte est un ouvrage didactique sur les bases de la géométrie avec quelques éléments relatifs à l'histoire.
• R. Pouzergues, Les Hexamys, IREM de Nice, IremOuvrage, 1993 Cote : IM8974 Lire
  Ce petit livre de 89 pages présente la géométrie projective. Il est disponible sur le net.
• D. Lehmann et Rudolf Bkouche, Initiation à la géométrie, PUF, 1988, (ISBN 2130401600)
  Ce livre de géométrie commence simplement. Il couvre ensuite l'utilisation d'outils plus sophistiqués comme les formes quadratiques. Il contient un Appendice historique.

• Y. Sortais, La Géométrie du triangle. Exercices résolus, Hermann, 1997, (ISBN 270561429X)
  Ce livre s'adresse essentiellement aux élèves de la seconde à la terminale, ainsi qu'à leur professeur. Il propose des exercices sur le théorème de Thalès, la projection orthogonale, l'homothétie, la symétrie et la rotation, le calcul barycentrique, le produit scalaire, ou encore la notion d'angle.
• Y. Ladegaillerie, Géométrie pour le CAPES de mathématiques, Ellipses Marketing, 2002 (ISBN 2729811486)
  Ce livre traite de géométrie élémentaire au programme du CAPES. Il contient plus de 600 figures géométriques et couvre la géométrie affine euclidienne ainsi que l'algèbre linéaire élémentaire.
• J. Perez, Mécanique physique, Masson, 2007 (ISBN 2225553416)
  Ce livre est un cours de physique a l'usage de la licence, il couvre les notions de torseur, vecteur lié, glissant et libre.
• M. B. Karbo, Le graphisme et l'internet, Compétence micro, n^o 26, 2002 (ISBN 2912954959)
  Ce livre traite à la fois des aspects pratiques comme la force et la faiblesse des différentes techniques, des différents logiciels et formats disponibles sur les marchés et des aspects théoriques

• Portail de l’algèbre
• Portail de la géométrie