Groupe des quaternions

En mathématiques et plus précisément en théorie des groupes, le groupe des quaternions est l'un des deux groupes non abéliens d'ordre 8.

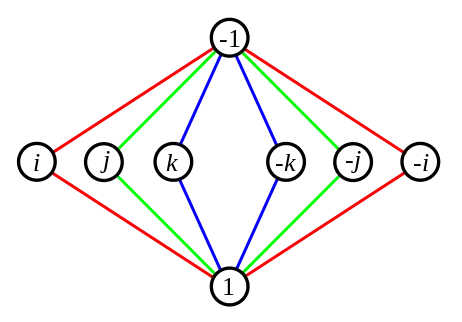
Graphe des cycles de Q. Chaque couleur précise une série de puissances d'un élément quelconque connecté à l'élément neutre (1). Par exemple, le cycle rouge reflète le fait que i ² = -1, i ³ = -i et i ⁴ = 1. Le cycle rouge reflète aussi le fait que (-i )² = -1, (-i )³ = i et (-i )⁴ = 1.

Il admet une représentation réelle irréductible de degré 4, et la sous-algèbre des matrices 4×4 engendrée par son image est un corps gauche qui s'identifie au corps des quaternions de Hamilton.

Définition

Le groupe des quaternions est souvent désigné par le symbole Q ou Q₈ et est écrit sous forme multiplicative, avec les 8 éléments suivants :

Q=\{1,-1,i,-i,j,-j,k,-k\}.

Ici, 1 est l'élément neutre, $(-1)^{2}=1\,$ et $(-1).a=a.(-1)=-a\,$ pour tout a dans Q. Les règles de multiplication restantes peuvent être obtenues à partir de l'associativité et de la relation suivante :

i^{2}=j^{2}=k^{2}=ijk=-1\,

Table du groupe

La table de multiplication pour Q est donnée par :

	1	i	j	k	-1	-i	-j	-k
1	1	i	j	k	-1	-i	-j	-k
i	i	-1	k	-j	-i	1	-k	j
j	j	-k	-1	i	-j	k	1	-i
k	k	j	-i	-1	-k	-j	i	1
-1	-1	-i	-j	-k	1	i	j	k
-i	-i	1	-k	j	i	-1	k	-j
-j	-j	k	1	-i	j	-k	-1	i
-k	-k	-j	i	1	k	j	-i	-1

Le groupe ainsi obtenu est non abélien, comme on peut le voir sur la relation $ij=-ji\,$ . Cependant Q est un groupe hamiltonien : tout sous-groupe de Q est normal, mais Q est non abélien. Tout groupe hamiltonien contient une copie de Q.

Propriétés

Représentation

Considérant un espace vectoriel réel de dimension 4 dont une base est notée {1, i, j, k}, on le munit d'une structure d'algèbre associative en utilisant la table de multiplication ci-dessus et la distributivité. Le résultat est un corps gauche appelé le corps des quaternions. Le lemme de Schur généralise cette approche. Il montre en effet que l'algèbre (associative) des endomorphismes de toute représentation irréductible d'un groupe est une algèbre à division donc un corps, parfois non commutatif.

Inversement, on peut démarrer avec le corps des quaternions et définir le groupe des quaternions comme le sous-groupe multiplicatif constitué des 8 éléments ${1,-1,i,-i,j,-j,k,-k}\,$ .

Sur tout corps de caractéristique différente de 2, le théorème de Maschke réduit l'étude des représentations de Q à celle de ses représentations irréductibles.

Représentations rationnelles et réelles

Faisons l'inventaire plus précis des représentations irréductibles de Q, à coefficients rationnels (ou réels, par extension des scalaires), et la description de celle de degré 4 à laquelle il est fait implicitement allusion ci-dessus.

On construit la représentation régulière λ (à coefficients rationnels) du groupe Q et de son algèbre ℚ[Q] en les faisant agir sur ℚ[Q] par multiplication à gauche. Comme toute représentation régulière d'algèbre unifère, λ est fidèle (car λ(x)(1) = x). Notons (δ_g)_g∈Q la base canonique de l'espace vectoriel ℚ[Q] ≃ ℚ^Q ≃ ℚ⁸.
La somme v₁ des 8 vecteurs de cette base est fixe par tous les λ(g) donc la sous-représentation λ₁, sur la droite vectorielle V₁ := ℚv₁, est la représentation unité de Q.
Il existe trois autres droites stables et sous-représentations de degré 1, notées V_q = ℚv_q et λ_q pour q = i, j, k : par exemple, v_i := (δ₁ + δ_–1 + δ_i + δ_–i) – (δ_j + δ_–j + δ_k + δ_–k) est envoyé sur lui-même par λ(±1) et λ(±i), et sur son opposé par λ(±j) et λ(±k).
Enfin, les quatre vecteurs w_q := δ_q – δ_–q pour q = 1, i, j, k engendrent un sous-espace W de dimension 4 supplémentaire de la somme (directe) des quatre droites précédentes. On vérifie que W est stable par λ : pour tout g ∈ Q, λ(g)(w_q) = εw_q', où ε ∈ {+, –} et q' ∈ {1, i, j, k} sont déterminés par l'égalité (dans Q) gq = εq'. Dans la sous-représentation correspondante de l'algèbre (en) ℚ[Q], que nous noterons w, on remarque que w(δ_–q) = –w(δ_q), c'est-à-dire que w se factorise par une représentation w' de l'algèbre quotient H_ℚ des « quaternions à coefficients rationnels » (pour une description matricielle de w', voir la représentation des quaternions comme matrices 4×4 de réels). Cette représentation w' est simplement la représentation régulière de l'algèbre H_ℚ (dont l'espace vectoriel s'identifie naturellement à W). L'irréductibilité de w' (donc celle de w) vient du fait que tout élément non nul x de H_ℚ est inversible donc H_ℚx = H_ℚ.

La représentation régulière de Q est donc somme directe de cinq représentations irréductibles : quatre de degré 1 (non équivalentes) et une de degré 4. Le morphisme d'algèbres $\mathbb {Q} [Q]\to \mathbb {Q} ^{4}\oplus {\rm {H}}_{\mathbb {Q} },x\mapsto (\lambda _{1}(x),\lambda _{\rm {i}}(x),\lambda _{\rm {j}}(x),\lambda _{\rm {k}}(x),w(x)(1))$ est injectif donc (par comparaison des dimensions) c'est un isomorphisme.

Représentations complexes

Sur ℂ, le groupe Q a également cinq représentations irréductibles, calculées dans l'article détaillé : les quatre caractères réels λ₁, λ_i, λ_j, λ_k ci-dessus et une représentation ρ, de degré 2 donc non réelle (en) (c'est un exemple de représentation induite, que l'on peut expliciter matriciellement). L'algèbre ℂ[Q] est donc isomorphe à ℂ⁴⊕M₂(ℂ).

On peut remarquer que la représentation réelle w ci-dessus est équivalente à celle obtenue à partir de ρ en considérant ℂ² comme un espace réel de dimension 4, et que w⊗ℂ est équivalente à ρ ⊕ ρ.

Nature du groupe

Les trois éléments i, j et k sont tous d'ordre 4 dans Q et deux quelconques d'entre eux engendrent le groupe entier. Q admet la présentation

\langle x,y\mid x^{4}=1,x^{2}=y^{2},yxy^{-1}=x^{-1}\rangle

On peut prendre, par exemple, x = i et y = j.

Tous les sous-groupes propres de Q sont cycliques.

Le centre et le sous-groupe des commutateurs de Q est le sous-groupe {±1}. Le groupe quotient Q/{±1} est isomorphe au groupe de Klein V. Il y a cinq classes de conjugaison : {1}, {-1}, {i, -i}, {j, -j} et {k, -k}.

Le groupe des automorphismes intérieurs de Q est isomorphe à Q modulo son centre, et est par conséquent aussi isomorphe au groupe de Klein. Le groupe des automorphismes de Q est isomorphe au groupe symétrique S₄. Le groupe des automorphismes extérieurs de Q est alors S₄/V qui est isomorphe à S₃.

Le groupe des quaternions Q peut aussi être vu comme un sous-groupe normal d'indice 3 du groupe spécial linéaire SL(2, F₃)[1].

Groupe de quaternions généralisé

Les groupes de quaternions généralisés sont les 2-groupes dicycliques, c'est-à-dire que (pour n ≥ 3), le groupe de quaternions généralisé d'ordre 2ⁿ est le groupe de présentation

Q_{2^{n}}=\langle x,y\mid x^{2^{n-1}}=1,x^{2^{n-2}}=y^{2},yxy^{-1}=x^{-1}\rangle .

Le groupe de quaternions ordinaire correspond au cas n = 3. Le groupe $Q_{2^{n}}$ peut être réalisé comme le sous-groupe des quaternions unitaires engendré par $x=\cos \left({\tfrac {2\pi }{2^{n-1}}}\right)+i\sin \left({\tfrac {2\pi }{2^{n-1}}}\right)$ et $y=j$ .

Le quotient de $Q_{2^{n}}$ par son centre est isomorphe au groupe diédral $D_{2^{n-1}}$ [2] donc $Q_{2^{n}}$ est nilpotent de classe n – 1.

Les groupes de quaternions généralisés ont la propriété que chaque sous-groupe abélien est cyclique. On peut prouver[3] qu'un p-groupe fini possédant cette propriété (chaque sous-groupe abélien est cyclique) est soit un groupe cyclique, soit un groupe de quaternions généralisé.

Notes et références

(en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Quaternion group » (voir la liste des auteurs).

Pour une image, voir Visualisation de GL(2,p).
(en) Joseph J. Rotman (en), An Introduction to the Theory of Groups [détail des éditions], 1995, 4^e éd., exerc. 4.42, p. 88.
Pour une démonstration, voir par exemple (en) I. Martin Isaacs (en), Finite Group Theory, AMS, 2008 (lire en ligne), p. 278-284, théorème 6.12, p. 189 (dont le présent énoncé se déduit immédiatement), ou encore (en) Hans Kurzweil (de) et Bernd Stellmacher, The Theory of Finite Groups, An Introduction, Springer, 2004 (lire en ligne), énoncé 5.3.8, p. 115.

Voir aussi

Articles connexes

Quaternions de Hurwitz
Liste des petits groupes
Groupe de Heisenberg sur F₂ ≃ Groupe diédral D₈ (le seul autre groupe non abélien d'ordre 8, à isomorphisme près)

Liens externes

(en) Vipul Naik, « Quaternion group », sur groupprops
Bruno Vallette, « Le groupe ℍ₈ », 2009 (énoncé et corrigé d'un examen de L3 à l'université Nice-Sophia-Antipolis)

Portail de l’algèbre

Cet article est issu de Wikipedia. Le texte est sous licence Creative Commons - Attribution - Partage dans les Mêmes. Des conditions supplémentaires peuvent s'appliquer aux fichiers multimédias.

[1] Pour une image, voir Visualisation de GL(2,p).

[2] (en) Joseph J. Rotman (en), An Introduction to the Theory of Groups [détail des éditions], 1995, 4^e éd., exerc. 4.42, p. 88.

[3] Pour une démonstration, voir par exemple (en) I. Martin Isaacs (en), Finite Group Theory, AMS, 2008 (lire en ligne), p. 278-284, théorème 6.12, p. 189 (dont le présent énoncé se déduit immédiatement), ou encore (en) Hans Kurzweil (de) et Bernd Stellmacher, The Theory of Finite Groups, An Introduction, Springer, 2004 (lire en ligne), énoncé 5.3.8, p. 115.