Flèche du temps

La flèche du temps est une expression introduite en 1928 par Arthur Eddington pour décrire le phénomène selon lequel le temps semble s'écouler toujours dans la même direction. Cette expression recouvre un ensemble de théories qui explique pourquoi le temps s'écoule de manière unidirectionnelle.

Représentation schématisée des flèches psychologique, cosmologique et thermodynamique

La flèche du temps fait partie des problèmes non résolus de la physique et elle suscite plusieurs controverses. Ces dernières apparaissent en raison de l'invariance dimensionnelle des équations fondamentales de la physique, alors que, contrairement aux autres dimensions, le temps semble avoir une direction irréversible[1].

La flèche du temps peut être appliquée à plusieurs domaines, notamment dans ceux de la physique, des statistiques et de la cosmologie. Elle possède également un lien très fort avec la philosophie et la psychologie car elle est indissociable des perceptions humaines. Ne relevant que de théories, plusieurs hypothèses alternatives existent, telles que la flèche gravitationnelle du temps ainsi que le temps en tant qu'illusion.

Historique
Portrait d'Arthur Stanley Eddington.

Avant le principe de flèche du temps, Ludwig Boltzmann introduit la notion d'entropie en 1877. Son approche s'applique aux systèmes fermés ayant atteint un équilibre thermodynamique. Josiah Willard Gibbs a ensuite publié de nouvelles équations définissant l'entropie qui s'appliquent plus généralement. De là, d'autres physiciens ont étudié le temps pour en venir à la flèche du temps.

En 1907, le mathématicien polonais Hermann Minkowski développe la relativité restreinte et l'espace-temps dans un modèle qui sera nommé par la suite l'espace de Minkowski. Dans ce dernier, les quatre dimensions, soit trois spatiales et une temporelle, forment un tout[2]. Il traite donc les dimensions spatiales et temporelles de la même façon.

En 1928, Arthur S. Eddington, un astrophysicien britannique, critique ce modèle dans son livre The Nature of the Physical World. Il affirme que l'espace de Minkowski ne fait pas de différence entre le passé, le présent et le futur et qu'il manque une direction au temps[3].

Eddington propose donc une flèche du temps avec comme fondement que les résultats du hasard sont les seules choses qui ne peuvent être défaites. C'est une flèche qui pointe vers l'augmentation des éléments aléatoires. L'opposé est également vrai, c'est-à-dire que si les éléments aléatoires se raréfient, la flèche pointe alors vers le passé[4],[5].

Typologie des flèches du temps

Flèche thermodynamique
L'entropie croissante d'un système fermé mène à l'équilibre de ses constituantes. Ici, il est hautement improbable que les constituantes du soluté quittent les pourtours du verre et se retrouvent au centre de ce dernier. Les flèches du temps thermodynamique et statistiques pointent donc de gauche vers la droite et permettent de dire que l'image de gauche précède celle de droite.

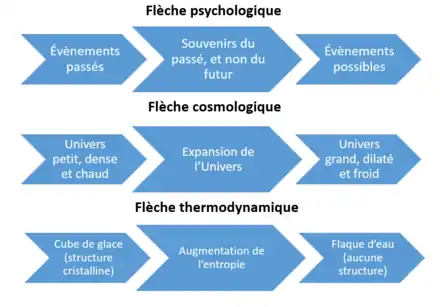
La flèche du temps thermodynamique est le sens donné au temps par la loi de l'entropie. Cette dernière dispose que le niveau d'entropie d'un système fermé qui n'est pas à l'équilibre thermodynamique doit augmenter. Par conséquent, il suffit de mesurer le niveau d'entropie d'un système fermé à deux instants différents pour savoir lequel précède l'autre. Si cette mesure est répétée à chaque instant, il apparaît une suite infinie d'états orientée dans une seule direction, c'est ce qui crée le sens du temps. Par conséquent, tout système fermé voit la direction de sa flèche temporelle déterminée par la différence d'entropie entre ses états[6].

La flèche thermodynamique permet d'établir la flèche statistique du temps. Ainsi, toujours dans un système fermé, cette dernière permet d'établir le mouvement temporel produit par une succession d'événements plus probables que d'autres. Plus un événement est improbable, plus il peut être relié à un passé ordonné. Inversement, plus il est probable, plus il peut être relié à un futur désordonné. Stephen Hawking illustre ce principe par « l'exemple du casse-tête ». Si un casse-tête terminé est dans une boite et que celle-ci est brassée, vraisemblablement le désordre augmentera puisqu'il y a énormément plus d'états où les pièces ne forment pas l'image du casse-tête[7].

La flèche du temps thermodynamique n'est pas éternelle. En effet, l'entropie ne peut augmenter en permanence dans un système fermé, elle finit par y trouver un équilibre où l'entropie atteint un maximum. Dans ce cas, le sens du temps disparait.

Flèche cosmologique
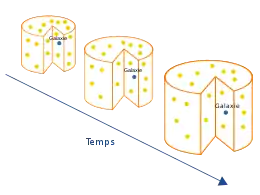
L'expansion de l'Univers imagée par le gonflement d'un pain aux raisins.

La flèche cosmologique du temps est le nom donné à l'application de la flèche thermodynamique ou statistique du temps à l'échelle de l'Univers. En effet, la deuxième loi de la thermodynamique ne fonctionne que pour un système fermé. Un niveau d'entropie qui diminue localement dans un système ouvert signifie simplement que l'entropie augmente de manière globale à l'extérieur du système. Cependant, il n'est pas déterminé si l'Univers est un système fermé ou non.

Si l'Univers est un système fermé, le temps peut être déterminé par une différence de niveau d'entropie. Cette hypothèse s'appelle l'« hypothèse du passé » car elle implique que l'état initial de l'Univers soit un cas particulièrement bas d'entropie. En croissant, l'entropie de l'univers atteindrait son maximum après une période de temps d'environ 10200 années[8]. Le temps perdra progressivement son sens jusqu'à disparaître.

Flèche gravitationnelle du temps

La flèche gravitationnelle du temps est une théorie alternative à la flèche cosmologique du temps. Elle s'appuie sur l'idée que l'Univers ne se dirige pas vers un niveau d'entropie de plus en plus élevé, mais vers un niveau structurel de complexité croissante. Elle s'oppose par conséquent à l'entropie qui détermine qu'un système fermé ne peut se diriger que vers un niveau de désordre de plus en plus élevé. Le sens du temps, du passé vers le futur, serait alors défini par la croissance irréversible de la complexité[9].

Flèche radiative
Émission dans toutes les directions
Cône de lumière
Émission d'ondes dans toutes les directions par une source ponctuelle et la représentation par un cône de lumière centré sur un événement.

La flèche radiative est décrite par le sens dans lequel un rayonnement quelconque est émis. Il est observable qu'une source n'émet pas dans des directions aléatoires, mais plutôt dans toutes les directions à la fois qui pointent vers l'extérieur de la source. Ce phénomène est exprimable par une sphère d'influence de la source ponctuelle. Cette sphère s'agrandit si le temps pointe vers l'avant, et diminue s'il pointe vers le passé. Cette schématisation est souvent utilisée en physique via le cône de lumière. Celui-ci ne présente un cercle s'agrandissant au lieu d'une sphère puisque la troisième dimension du graphique illustre la direction du temps[10].

Flèche conséquentielle
Schéma qui montre l'impossibilité dans certaines situations de déterminer la cause et la conséquence. Il est impossible de savoir lequel des deux personnages reçoit la balle et lequel l'a lancée.

La flèche du temps conséquentielle fait référence au principe de causalité à l'échelle macroscopique. Ce principe dispose que si un phénomène A produit un effet B, alors il en est la cause et l'effet ne peut jamais précéder sa cause. Ainsi, un sens est donné au temps de la cause vers la conséquence. Cette flèche du temps est fondamentale en sciences. En effet, la méthode scientifique s'appuie sur le fait que les mêmes causes produisent les mêmes conséquences.

Flèche psychologique

La flèche psychologique du temps est le sens donné au temps par les limites de la perception humaine. En effet, l'être humain détermine le temps par la différence entre un état 1 initial et un état 2 observé instantanément. Si aucun changement n'est constaté, un être humain ne saurait distinguer si le temps avance, recule ou même existe. L'être humain ne peut se remémorer que les événements qu'il a vécus, le passé, et le comparer au présent qui deviendra à son tour passé dès qu'un changement aura été enregistré par l'individu. Ce mouvement apparent crée le passage du temps du passé, soit ce que l'on peut comparer au présent, vers le futur[7].

La perception du temps est subjective et sujette, notamment, à plusieurs illusions (en). Ainsi, le temps peut sembler plus long lors de périodes d'ennui et plus court lors d'événements intenses. En fait, la perception du temps d'un observateur peut varier en fonction de ses émotions et de son âge[11].

Notes et références
  1. https://www.jstor.org/stable/43695560
  2. (en) « A Space-Time Cocktail: Minkowski Space and Special Relativity » (consulté le )
  3. Huw Price, Seminaire Poincare XV, Le Temps (2010) p. 115-140, (en) « Time's Arrow and Eddington's Challenge » (consulté le )
  4. (en) Arthur Eddington, The nature of the physical world, New York, The Macmillan Company; Cambridge, Eng., The University Press, , 396 p. (lire en ligne)
  5. (en) Friedel Weinert, The scientist as philosopher : philosophical consequences of great scientific discoveries, Springer, , 342 p. (ISBN 3-540-21374-0, lire en ligne), p. 143, Chapitre 4, p. 143
  6. Gold 1962, p. 404
  7. Stephen Hawking, Une brève histoire du temps : Du big bang aux trous noirs, France, Flammarion, coll. « Nouvelle bibliothèque scientifique », , 236 p. (ISBN 2-08-211182-2), p. 180-192
  8. (en) « THE BIG CRUNCH, THE BIG FREEZE AND THE BIG RIP » (consulté le )
  9. « Comment le temps file : suivre la flèche du temps. » (consulté le )
  10. (en) « Causality and the Light Cone » (consulté le )
  11. « Le temps et nous : notre temps subjectif » (consulté le )

Voir aussi

Bibliographie

 : document utilisé comme source pour la rédaction de cet article.

  • (en) Carlo Rovelli, « Is Time's Arrow Perspectival? », arxiv,‎ (lire en ligne, consulté le ).
  • (en) Petri Tuisku, Tuomas K Pernu et Arto Annila, « In the light of time », Proceeding of the Royal Society A, vol. 465, no 2104,‎ (lire en ligne, consulté le )
  • (en) Sean Carrol, « Cosmology and the arrow of time », sur YouTube, (consulté le ).
  • (en) T. Gold, « The arrow of time », American Journal of Physics, vol. 30,‎ , p. 403-410 (résumé).
  • Roger Balian ; Le temps macroscopique : texte d'une remarquable conférence sur l'irréversibilité et l'entropie donnée lors du premier colloque "Physique & Interrogations Fondamentales" : Le Temps et sa Flèche organisé par la Société Française de Physique le 8 décembre 1993 à Paris. Publié dans : Étienne Klein & Michel Spiro (éditeurs) ; Le Temps et sa Flèche, Les Éditions Frontières (1994), 155-211. Repris en poche par Flammarion, Collection Champs (1995).
  • Roger Balian ; Entropie, information : un concept protéiforme : texte d'une conférence donnée à l'Université de tous les savoirs (239e conférence : Les États de la matière, 26 août 2000, Conservatoire national des Arts et Métiers, Paris). Publiée par Yves Michaud (éditeur) ; Université de tous les savoirs (Vol. 4), Odile Jacob (2001), 947-959. Repris en édition de poche : Université de tous les savoirs (Vol. 17), Poches Odile Jacob (2002), 205-220
  • Roger Balian ; Entropy, a Protean Concept : texte d'une conférence donnée au séminaire Poincaré du 6 décembre 2003 consacré à l'entropie. Publié dans : J. Dalibard, B. Duplantier et V. Rivasseau (eds.) ; Poincaré seminar 2003: Bose--Einstein condensation - Entropy, Progress in Mathematical Physics 38, Birkhäuser (2004), (ISBN 3-7643-7106-4).
  • Olivier Darrigol ; The origins of the entropy concept : texte d'une conférence introductive donnée par l'auteur (REHSEIS-CNRS) au séminaire Poincaré du 6 décembre 2003 consacré à l'entropie. Publié dans : J. Dalibard, B. Duplantier et V. Rivasseau (eds.) ; Poincaré seminar 2003: Bose--Einstein condensation - Entropy, Progress in Mathematical Physics 38, Birkhäuser (2004), (ISBN 3-7643-7106-4).
  • (en) Hans Dieter Zeh, The physical basis of the direction of time, Berlin New York, Springer, (réimpr. 2007), 4e éd. (1re éd. 1989), 231 p. (ISBN 978-3-540-42081-1, OCLC 46791089, lire en ligne).
  • (en) Jonathan J Halliwell, J. Pérez-Mercader et Wojciech Hubert Zurek, Physical origins of time asymmetry, Cambridge England New York, Cambridge University Press, , 515 p. (ISBN 978-0-521-56837-1 et 978-0-521-43328-0, OCLC 36415828, lire en ligne).
  • (en) Hans Reichenbach et Maria Reichenbach (éditeur), The direction of time, Mineola, N.Y, Dover, , 280 p. (ISBN 978-0-486-40926-9, OCLC 954098947, lire en ligne).
  • Sean Carroll (trad. de l'anglais), L'Univers et la flèche du temps [« From Eternity to Here : The Quest for the Ultimate Theory of Time »], Quanto, (ISBN 978-2-88915-432-6).

Articles connexes
  • Portail de la physique
  • Portail de la cosmologie
Cet article est issu de Wikipedia. Le texte est sous licence Creative Commons - Attribution - Partage dans les Mêmes. Des conditions supplémentaires peuvent s'appliquer aux fichiers multimédias.