Position du Soleil
La position du Soleil dans le ciel est fonction à la fois du temps et de l'emplacement géographique de l'observation à la surface de la Terre. Alors que la Terre orbite autour du Soleil au cours d'une année, le Soleil semble se déplacer par rapport aux étoiles fixes de la sphère céleste, le long d'une trajectoire circulaire appelée écliptique.
La rotation de la Terre autour de son axe provoque un mouvement diurne ; de sorte que le Soleil se déplace apparemment à travers le ciel sur une trajectoire solaire et que les étoiles fixes se déplacent apparemment à travers le ciel, d'une manière qui dépend de la latitude géographique de l'observateur. Le moment où une étoile fixe donnée transite par le méridien de l'observateur dépend de la longitude géographique.
Pour trouver la position du Soleil pour un lieu donné à un instant donné, on peut donc procéder en trois étapes comme suit[1],[2] :
- Calculer la position du Soleil dans le système de coordonnées écliptiques ;
- Convertir en système de coordonnées équatoriales ;
- Convertir au système de coordonnées horizontales, pour l'heure et l'emplacement locaux de l'observateur.
Ce calcul est utile en astronomie, pour la navigation, l'arpentage, la météorologie, la climatologie, l'énergie solaire et la conception de cadrans solaires et aussi pour les astrolabes planisphérique.
Position approximative
Coordonnées écliptiques
Ces équations, tirées de l'Almanach astronomique[3],[4], peuvent être utilisées pour calculer les coordonnées apparentes du Soleil, l'équinoxe moyen et l'écliptique de la date, avec une précision d'environ 0° 0,01' (soit 36 secondes d'arc), pour les dates comprises entre 1950 et 2050.
On commence par calculer n, le nombre de jours (positifs ou négatifs) depuis midi de Greenwich, heure terrestre, le (J2000.0). Si on connaît la date julienne pour l'heure souhaitée,
La longitude moyenne du Soleil, corrigée de l'aberration de la lumière, est :
L'anomalie moyenne du Soleil (en fait, de la Terre dans son orbite autour du Soleil, mais il est commode de prétendre que le Soleil tourne autour de la Terre), est :
Mettre et dans la plage de 0° à 360° en ajoutant ou en soustrayant des multiples de 360° selon les besoins.
Enfin, la longitude écliptique du Soleil est :
La latitude écliptique du Soleil est presque :
- ,
comme la latitude écliptique du Soleil ne dépasse jamais 0,00033°[5],
et la distance du Soleil à la Terre, en unités astronomiques, est :
- .
Coordonnées équatoriales
, et caractérisent complètement la position du Soleil dans le système de coordonnées écliptiques. Ils peuvent être convertis dans le système de coordonnées équatoriales en calculant :
- l'obliquité de l'écliptique, ;
- l'ascension droite , où est dans le même quadrant que . Pour obtenir l'ascension droite dans le bon quadrant , on utilise la fonction arc tangente à double argument (atan2(y,x) dans de nombreux langages informatiques) : ;
- et la déclinaison, .
Coordonnées équatoriales rectangulaires
En coordonnées équatoriales rectangulaires à droite (où le l'axe est dans la direction du point vernal, et le l'axe est de 90° à l'est, dans le plan de l'équateur céleste, et le l'axe est dirigé vers le pôle nord céleste[6]), en unités astronomiques :
Obliquité de l'écliptique
Lorsque l'obliquité de l'écliptique n'est pas obtenue ailleurs, elle peut être approximée :
à utiliser avec les équations ci-dessus.
Déclinaison du Soleil, vu de la Terre

Aperçu
Le Soleil semble se déplacer vers le nord pendant le printemps nordique, en contact avec l'équateur céleste lors de l'équinoxe de mars. Sa déclinaison atteint un maximum égal à l'angle d'inclinaison axiale de la Terre (23,44°)[7],[8] au solstice de juin, puis diminue jusqu'à atteindre son minimum (−23,44°) au solstice de décembre, lorsque sa valeur est le négatif de l'inclinaison axiale. Cette variation produit les saisons.
Un graphique linéaire de la déclinaison du Soleil au cours d'une année ressemble à une onde sinusoïdale d'une amplitude de 23,44°, mais un lobe de la vague est plusieurs jours plus long que l'autre, entre autres différences.
Les phénomènes suivants se produiraient si la Terre est une sphère parfaite, dans une orbite circulaire autour du Soleil, et si son axe est incliné à 90°, de sorte que l'axe lui-même est sur le plan orbital (similaire à Uranus). À une date de l'année, le Soleil serait directement au-dessus du pôle Nord, donc sa déclinaison serait de +90°. Au cours des prochains mois, le point subsolaire se déplacerait vers le pôle Sud à vitesse constante, traversant les cercles de latitude à un rythme constant, de sorte que la déclinaison solaire diminuerait linéairement avec le temps. Finalement, le Soleil serait directement au-dessus du pôle Sud, avec une déclinaison de –90° ; alors il commencerait à se déplacer vers le nord à une vitesse constante. Ainsi, le graphique de la déclinaison solaire, vu de cette Terre très inclinée, ressemblerait à une onde triangulaire plutôt qu'à une onde sinusoïdale, zigzaguant entre plus et moins 90°, avec des segments linéaires entre les maxima et les minima.
Si l'inclinaison axiale à 90° est diminuée, les valeurs absolues maximale et minimale de la déclinaison diminueraient, pour égaler l'inclinaison axiale. De plus, les formes des maxima et des minima sur le graphique deviendraient moins aiguës (« pointues »), étant incurvées pour ressembler aux maxima et aux minima d'une onde sinusoïdale. Cependant, même lorsque l'inclinaison axiale est égale à celle de la Terre réelle, les maxima et les minima restent plus aigus que ceux d'une onde sinusoïdale.
En réalité, l'orbite de la Terre est elliptique. La Terre se déplace plus rapidement autour du Soleil près du périhélie, début janvier, que près de l'aphélie, début juillet. Cela accélère les processus comme la variation de la déclinaison solaire en janvier qu'en juillet. Sur le graphique, cela rend les minima plus aigus que les maxima. De plus, comme le périhélie et l'aphélie ne se produisent pas aux dates exactes comme les solstices, les maxima et les minima sont légèrement asymétriques. Les taux de variation avant et après ne sont pas tout à fait égaux.
Le graphique de la déclinaison solaire apparente est donc différent à plusieurs égards d'une onde sinusoïdale. Le calculer avec précision implique une certaine complexité, comme indiqué ci-dessous.
Calculs

La déclinaison du Soleil, δ ☉, est l'angle entre les rayons du Soleil et le plan de l'équateur terrestre. L'inclinaison axiale de la Terre (appelée obliquité de l'écliptique par les astronomes) est l'angle entre l'axe de la Terre et une ligne perpendiculaire à l'orbite de la Terre. L'inclinaison axiale de la Terre change lentement au cours des milliers d'années, mais sa valeur actuelle d'environ ε = 23° 26' est presque constante, de sorte que le changement de déclinaison solaire au cours d'une année est presque le même que l'année suivante.
Aux solstices, l'angle entre les rayons du Soleil et le plan de l'équateur terrestre atteint sa valeur maximale de 23° 26'. Par conséquent, δ ☉ = + 23° 26' au solstice d'été nord et δ ☉ = −23° 26' au solstice d'été sud.
Au moment de chaque équinoxe, le centre du Soleil semble passer par l'équateur céleste, et δ☉ vaut 0°.
La déclinaison du Soleil à un moment donné est calculée par :
où LÉ est la longitude écliptique (essentiellement, la position de la Terre sur son orbite). Étant donné que l'excentricité orbitale de la Terre est petite, son orbite peut être approximée comme un cercle qui provoque jusqu'à 1° d'erreur. L'approximation du cercle signifie que l'EL serait à 90° devant les solstices de l'orbite terrestre (aux équinoxes), de sorte que sin (EL) peut s'écrire sin (90 + NDS) = cos (NDS) où NDS est le nombre de jours après le solstice de décembre. En utilisant également l'approximation selon laquelle arcsin [sin (d) · cos (NDS)] est proche de d · cos (NDS), la formule fréquemment utilisée suivante est obtenue :
où N est le jour de l'année commençant par N = 0 à minuit, heure universelle (UT) au début du (c'est-à-dire la partie jours de la date ordinale -1). Le nombre 10, en (N + 10), est le nombre approximatif de jours après le solstice de décembre jusqu'au . Cette équation surestime la déclinaison proche de l'équinoxe de septembre jusqu'à + 1,5°. L'approximation de la fonction sinusoïdale conduit en soi à une erreur allant jusqu'à 0,26° et a été déconseillée pour une utilisation dans les applications d'énergie solaire[2]. La formule de Spencer de 1971[9] (basée sur une série de Fourier) est également déconseillée pour avoir une erreur allant jusqu'à 0,28°[10]. Une erreur supplémentaire allant jusqu'à 0,5° peut se produire dans toutes les équations autour des équinoxes si on n'utilise pas de décimale lorsqu'on sélectionne N pour ajuster le temps après UT minuit pour le début de la journée. Ainsi, l'équation ci-dessus peut avoir jusqu'à 2,0° d'erreur, environ quatre fois la largeur angulaire du soleil, selon la façon dont elle est utilisée.
La déclinaison peut être calculée avec plus de précision en ne faisant pas les deux approximations, en utilisant les paramètres de l'orbite de la Terre pour estimer plus précisément EL[11] :
qui peut être simplifié en évaluant les constantes pour :
N est le nombre de jours depuis minuit (temps universel) au début du (c'est-à-dire la partie jours de la date ordinale -1) et peut inclure des décimales pour s'adapter aux heures locales plus tard ou plus tôt dans la journée. Le nombre 2, en (N-2), est le nombre approximatif de jours après le jusqu'au périhélie de la Terre. Le nombre 0,0167 est la valeur actuelle de l'excentricité de l'orbite terrestre. L'excentricité varie très lentement dans le temps, mais pour des dates assez proches du présent, elle peut être considérée comme constante. Les plus grandes erreurs dans cette équation sont inférieures à ±0,2°, mais inférieures à ±0,03° pour une année donnée si le nombre 10 est ajusté à la hausse ou à la baisse en jours fractionnaires, comme déterminé par la distance du solstice de décembre de l'année précédente avant ou après midi le 22 décembre. Ces précisions sont comparées aux calculs avancés de la NOAA[12],[13] qui sont basés sur l'algorithme Jean Meeus de 1999 qui est précis à 0,01° près[14].
(La formule ci-dessus est liée à un calcul raisonnablement simple et précis de l'équation du temps, qui est décrit ici.)
Des algorithmes plus complexes[15],[16] corrigent les modifications de la longitude écliptique en utilisant des termes en plus de la correction d'excentricité de premier ordre ci-dessus. Ils corrigent également l'obliquité de 23,44° qui change très légèrement avec le temps. Les corrections peuvent également inclure les effets de la lune en décalant la position de la Terre par rapport au centre de l'orbite de la paire autour du Soleil. Après avoir obtenu la déclinaison par rapport au centre de la Terre, une autre correction de parallaxe est appliquée, qui dépend de la distance de l'observateur par rapport au centre de la Terre. Cette correction est inférieure à 0,0025°. L'erreur dans le calcul de la position du centre du Soleil peut être inférieure à 0,00015°. À titre de comparaison, la largeur du Soleil est d'environ 0,5°.
Réfraction atmosphérique
Les calculs de déclinaison décrits ci-dessus n'incluent pas les effets de la réfraction de la lumière dans l'atmosphère, ce qui fait que l'angle d'élévation apparent du Soleil vu par un observateur est plus élevé que l'angle d'élévation réel, en particulier à faible élévation du Soleil[2]. Par exemple, lorsque le Soleil est à une altitude de 10°, il semble être à 10,1°. La déclinaison du Soleil peut être utilisée, avec son ascension droite, pour calculer son azimut et aussi sa véritable élévation, qui peut ensuite être corrigée pour la réfraction pour donner sa position apparente[13],[17].
Équation du temps
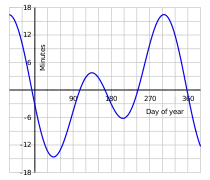
En plus de l'oscillation annuelle nord-sud de la position apparente du Soleil, correspondant à la variation de sa déclinaison décrite ci-dessus, il existe également une oscillation plus petite mais plus complexe dans la direction est-ouest. Cela est dû à l'inclinaison de l'axe de la Terre et également aux changements de vitesse de son mouvement orbital autour du Soleil produits par la forme elliptique de l'orbite. Les principaux effets de cette oscillation est-ouest sont des variations dans le calendrier d'événements tels que le lever et le coucher du soleil, et dans la lecture d'un cadran solaire par rapport à une horloge indiquant l'heure moyenne locale. Comme le montre le graphique, un cadran solaire peut avoir jusqu'à environ 16 minutes d'avance ou de retard par rapport à une horloge. Puisque la Terre tourne à une vitesse moyenne d'un degré toutes les 4 minutes par rapport au Soleil, ce déplacement de 16 minutes correspond à un décalage vers l'est ou vers l'ouest d'environ quatre degrés dans la position apparente du Soleil par rapport à sa position moyenne. Un décalage vers l'ouest fait que le cadran solaire est en avance sur l'horloge.
Comme le principal effet de cette oscillation concerne le temps, on l'appelle l'équation du temps, en utilisant le mot « équation » dans un sens quelque peu archaïque signifiant « correction ». L'oscillation est mesurée en unités de temps, minutes et secondes, correspondant au temps d'avance qu'un cadran solaire aurait sur une horloge. L'équation du temps peut être positive ou négative.
Analemme

Un analemme est un diagramme qui montre la variation annuelle de la position du Soleil sur la sphère céleste, par rapport à sa position moyenne, vue depuis un emplacement fixe sur Terre. (Le mot analemme est aussi parfois, mais rarement, utilisé dans d'autres contextes.) Il peut être considéré comme une image du mouvement apparent du Soleil pendant une année, qui ressemble à une figure en forme de 8. Un analemme peut être représenté en superposant des photographies prises au même moment de la journée, à quelques jours d'intervalle pendant un an.
Un analemme peut également être considéré comme un graphique de la déclinaison du Soleil, généralement tracé verticalement, par rapport à l'équation du temps, tracée horizontalement. Habituellement, les échelles sont choisies de sorte que des distances égales sur le diagramme représentent des angles égaux dans les deux directions sur la sphère céleste. Ainsi 4 minutes d'arc (plus précisément 3 minutes, 56 secondes), dans l'équation du temps, sont représentées par la même distance que 1° dans la déclinaison, puisque la Terre tourne à une vitesse moyenne de 1° toutes les 4 minutes, par rapport au Soleil.
Un analemme est dessiné tel qu'il serait vu dans le ciel par un observateur regardant vers le haut. Si le nord est indiqué en haut, alors l'ouest est à droite. Cela se fait généralement même lorsque l'analemme est marqué sur un globe géographique, sur lequel les continents, par exemple, sont représentés l'ouest à gauche.
Certains analemmes sont marqués pour montrer la position du Soleil sur le graphique à différentes dates, à quelques jours d'intervalle, tout au long de l'année. Cela permet à l'analemme d'être utilisé pour effectuer de simples calculs analogiques de quantités telles que les heures et les azimuts du lever et du coucher du soleil. Des analogies sans marquage de date sont utilisées pour corriger l'heure indiquée par les cadrans solaires.
Références
- (en) Jean Meeus, Astronomical Algorithms, Richmond, VA, Willmann Bell, Inc., , 429 p. (ISBN 0-943396-35-2), « Chapter 12: Transformation of Coordinates »
- A. Jenkins, « The Sun's position in the sky », The European Physical Journal, vol. 34, no 3, , p. 633 (DOI 10.1088/0143-0807/34/3/633, Bibcode 2013EJPh...34..633J, arXiv 1208.1043)
- La plupart du même jeu d'équations, couvrant les années 1800 à 2200, peuvent être trouvées aux coordonnées solaires approximatives (Approximate Solar Coordinates), sur le site de l'U.S. Naval Observatory « https://web.archive.org/web/20160131231447/http://www.usno.navy.mil/USNO »(Archive.org • Wikiwix • Archive.is • Google • Que faire ?), . Les graphiques de l'erreur de ces équations, comparées à une éphéméride précise, peuvent également être consultés.
- Meeus (1991), p. 152
- « Selected Astronomical Constants, 2015 » [PDF], US Naval Observatory, , K6–K7
- « Selected Astronomical Constants, 2015 » [txt], US Naval Observatory, , K6–K7
- (en) J. W. Spencer, « Fourier series representation of the position of the sun », Search, vol. 2, no 5, , p. 172 (lire en ligne)
- Alistair B. Sproul, « Derivation of the solar geometric relationships using vector analysis » (consulté le )
- « SunAlign » [archive du ] (consulté le )
- « NOAA Solar Calculator », Earth System Research Laboratory (consulté le )
- « Solar Calculation Details », Earth System Research Laboratory (consulté le )
- « Astronomical Algorithms » (consulté le )
- Manuel Blanco-Muriel, Diego C Alarcón-Padilla, Teodoro López-Moratalla et Martín Lara-Coira, « Computing the Solar Vector », Solar Energy, vol. 70, no 5, , p. 431–441 (DOI 10.1016/s0038-092x(00)00156-0, Bibcode 2001SoEn...70..431B, lire en ligne)
- Ibrahim Reda et Afshin Andreas, « Solar Position Algorithm for Solar Radiation Applications » (consulté le )
- « Atmospheric Refraction Approximation », National Oceanic and Atmospheric Administration (consulté le )
Voir aussi
Articles connexes
- Écliptique
- Effet de l'inclinaison du soleil sur le climat
- Paramètres de Milanković
- Les tables solaires de Newcomb
- Angle azimutal solaire
- Angle d'élévation solaire
- Éclairement énergétique
- Temps solaire
- Trajectoire solaire dans le ciel
- Équations de lever du soleil
Liens externes
- Solar Position Algorithm, sur le site du Renewable Resource Data Center du National Renewable Energy Laboratory.
- Sun Position Calculator, sur pveducation.org. Une calculatrice interactive montrant la trajectoire du soleil dans le ciel.
- NOAA Solar Calculator, sur le site de la division de surveillance mondiale du laboratoire de recherche sur les systèmes terrestres de la NOAA.
- Calculateur de déclinaison et de position du soleil de la NOAA
- Système HORIZONS, sur le site du JPL. Positions très précises des objets du système solaire basées sur les éphémérides de la série JPL DE.
- Éphémérides générales des corps du système solaire, sur le site de l' IMCCE. Positions d'objets du système solaire basées sur les éphémérides de la série INPOP.
- Position solaire dans le package R. Insol.
- Portail de l’astronomie
