Vitesse de la lumière
La vitesse de la lumière dans le vide, habituellement notée c, est une constante physique de l'Univers qui est importante dans plusieurs domaines de la physique. L'étude de la lumière et de sa vitesse remonte à l'Antiquité. Des philosophes et des scientifiques, en s'appuyant sur des arguments théoriques ou des observations, affirment que sa vitesse est infinie, alors que d'autres prétendent que non. C'est en 1676 qu'Ole Rømer démontre qu'elle est finie. Les scientifiques s'attachent ensuite à déterminer sa valeur par divers moyens. Vers la fin du XXe siècle, sa valeur exacte est établie à 299 792 458 mètres par seconde (environ 300 000 km/s)[note 1] à la suite d'un accord international.
| Unités SI | mètre par seconde (m/s ou m s−1) |
|---|---|
| Autres unités | CGS : centimètre par seconde (cm/s ou cm s−1) |
| Dimension | |
| Nature | Grandeur scalaire |
| Symbole usuel | c |
| Valeur | 299 792 458 m/s |
Le philosophe grec Héron d'Alexandrie (qui a vécu au 1er siècle) affirme, en s'appuyant sur la théorie de l'émission, que la vitesse de la lumière est infinie. Par la suite, des philosophes et des scientifiques tentent de déterminer si elle est finie ou infinie. Ole Rømer démontre le premier, en 1676, que la lumière a une vitesse finie en étudiant le mouvement apparent de la lune Io de Jupiter. En 1865, James Clerk Maxwell propose que la lumière soit une onde électromagnétique ; dans le cadre de sa théorie électromagnétique, la vitesse de la lumière est donc c. Au début du XXe siècle, Albert Einstein postule que la vitesse de la lumière est une constante, peu importe le référentiel inertiel où elle est observée, et qu'elle est indépendante de la vitesse de la source lumineuse. Ces postulats lui permettent de jeter les bases de la théorie de la relativité restreinte en 1905. Selon cette théorie, c relie l'espace et le temps ; elle apparaît aussi dans , « fameuse équation »[1] qui relie la masse à l'énergie.
Après des siècles de mesures de plus en plus précises, la vitesse de la lumière dans le vide est établie en 1975 à la valeur de 299 792 458 m/s avec une incertitude de 4 parties par milliard. En 1983, le mètre est redéfini dans le Système international d'unités (SI) en fonction de c.
Dans la vie de tous les jours, la lumière (et donc les ondes électromagnétiques) semble se déplacer instantanément, mais sur de longues distances ou dans des instruments de mesure très précis, des effets permettent de déduire que sa vitesse est finie. Dans les matériaux transparents et les conducteurs électriques, les ondes électromagnétiques se déplacent plus lentement que c. Les vitesses de certains phénomènes ondulatoires et de certains objets célestes peuvent être plus grandes que c. La vitesse d'expansion de l'Univers excède c hors de certaines limites géométriques.
Bien que cette vitesse soit le plus souvent associée à la lumière, c'est aussi celle de toute particule sans masse et de toute perturbation dans un champ situé dans le vide, incluant les ondes gravitationnelles et les ondes électromagnétiques (dont la lumière visible ne constitue qu'une minuscule partie). Les particules dotées d'une masse au repos peuvent approcher de c, mais ne peuvent l'atteindre, peu importe le référentiel inertiel dans lequel leur vitesse est mesurée.
Définitions
Au XXIe siècle, la vitesse de la lumière dans le vide est dénotée par la lettre minuscule c, abréviation de « constante », du mot latin celeritas (signifiant « rapidité, célérité ») ou encore de « célérité » en français, mais son symbole a varié dans le temps. En 1856, Wilhelm Eduard Weber et Rudolf Kohlrausch utilisent c pour une constante différente qui a été plus tard démontrée égale à √2 × c. En 1865, le symbole V est introduit par James Clerk Maxwell comme alternative pour indiquer la vitesse de la lumière dans le vide. En 1894, Paul Drude préfère c, tout en lui donnant sa définition moderne. Pourtant, Albert Einstein utilise V dans ses articles sur la relativité restreinte de 1905 ; c'est en 1907 qu'il commence à utiliser c, devenu entretemps le symbole courant pour la vitesse de la lumière dans le vide[2],[3],[4].
Parfois, c est utilisée pour indiquer la vitesse d'une onde lumineuse dans n'importe quel médium physique et c0 pour la vitesse de la lumière dans le vide[5]. Cette notation indicée, présente dans la littérature du SI[6], a la même forme que plusieurs constantes de l'électromagnétisme : μ0 pour la perméabilité du vide (ou constante magnétique), ε0 pour la permittivité du vide (ou constante électrique) et Z0 pour l'impédance caractéristique du vide. Dans la suite de cet article, seul c est utilisé pour désigner la vitesse de la lumière dans le vide.
Histoire
Avant l'époque moderne (grossièrement, de 1500 à 1800), des scientifiques et des philosophes proposent soit que la lumière se déplace instantanément soit à une vitesse finie très grande. Le premier enregistrement connu d'un effort dans ce sens remonte à la Grèce antique. Les Grecs anciens, les érudits musulmans puis les scientifiques européens de l'époque moderne ont longuement débattu sur ce sujet, jusqu'à ce que Ole Rømer fournisse la première preuve que la vitesse de la lumière est finie. La relativité restreinte d'Einstein, proposée en 1905 et vérifiée expérimentalement par la suite, permet de conclure que c est constante, peu importe le référentiel où elle est mesurée. Au XXe siècle, des scientifiques ont continué à affiner la valeur de c.
| <1638 | Galilée, lanternes masquées | pas concluant[7],[8],[9],[note 2] | |
| <1667 | Accademia del Cimento, lanternes masquées | pas concluant[10],[11] | |
| 1675 | Rømer et Huygens, lune Io de Jupiter | 220 000[12],[13] | erreur de ‒27 % |
| 1729 | James Bradley, aberration de la lumière | 301 000[14] | erreur de +0,40 % |
| 1849 | Hippolyte Fizeau, roue dentelée en rotation | 315 000[14] | erreur de +5,1 % |
| 1862 | Léon Foucault, miroirs rotatifs | 298 000 ± 500[14] | erreur de ‒0,60 % |
| 1907 | Rosa et Dorsey, constantes électromagnétiques et | 299 710 ± 30[15],[16] | erreur de ‒280 ppm |
| 1926 | Albert Michelson, miroir rotatif | 299 796 ± 4[17] | erreur de +12 ppm |
| 1950 | Essen et Gordon-Smith, cavité résonnante | 299 792,5 ± 3,0[18] | erreur de +0,14 ppm |
| 1958 | K. D. Froome, interférométrie radio | 299 792,50 ± 0,10[19] | erreur de +0,14 ppm |
| 1972 | Evenson et al., interférométrie laser | 299 792,456 2 ± 0,001 1[20] | erreur de ‒0,006 ppm |
| 1983 | 17e congrès de la CGPM, définition du mètre | 299 792,458[21] | exact, par définition |
Premières tentatives d'explications
Empédocle (c. 490-430 av. J.-C.) est le premier à proposer une théorie de la lumière[22] et déclare que la lumière a une vitesse finie[23]. Il affirme que la lumière est quelque chose en mouvement, et doit donc prendre du temps pour voyager. Aristote, au contraire, argue que « la lumière est due à la présence de quelque chose, mais ce n'est pas un mouvement »[trad 1],[24]. Euclide et Ptolémée reprennent la théorie de l'émission d'Empédocle, où la lumière provient de l'œil, ce qui permet de voir. En se basant sur cette théorie, Héron d'Alexandrie affirme que la vitesse de la lumière doit être infinie puisque l'on voit des objets distants, telles les étoiles, dès que l'on ouvre les yeux[25].
Les premiers philosophes islamiques acceptent dans un premier temps la vision aristotélicienne selon laquelle la lumière ne voyage pas. En 1021, Alhazen publie son Traité d'optique, où il présente un ensemble d'arguments contre la théorie de l'émission et en faveur de la théorie de l'intromission, c'est-à-dire que la lumière d'un objet entre dans l’œil[26]. Sa réflexion l'amène à proposer que la lumière doit voyager à une vitesse finie[24],[27],[28] et que cette vitesse peut changer selon le corps dans lequel elle se propage, étant plus lente dans les corps plus denses[28],[29]. Il soutient que la lumière est une matière faite d'une substance solide, sa propagation exige donc du temps, même si nos sens ne peuvent le percevoir[30]. Également au XIe siècle, Al-Biruni soutient que la vitesse de la lumière est finie et mentionne qu'elle est nettement plus grande que celle du son[31].
Au XIIIe siècle, Roger Bacon argue que la vitesse de la lumière dans l'air n'est pas infinie, recourant à des arguments philosophiques qui s'appuient sur les travaux d'Alhazen et d'Aristote[32],[33]. Dans les années 1270, Vitellion étudie la possibilité que la lumière voyage à une vitesse infinie dans le vide, mais ralentit dans les corps plus denses[34].
Au début du XVIIe siècle, Johannes Kepler pense que la vitesse de la lumière est infinie puisque l'espace vide ne présente aucun obstacle à sa propagation. René Descartes argue que si la vitesse de la lumière est finie, le Soleil, la Terre et la Lune ne seraient pas parfaitement alignés lors d'une éclipse lunaire. Puisqu'un tel manque d'alignement n'a pas été observé, Descartes conclut que la vitesse de la lumière est infinie. Il spécule que si la vitesse de la lumière était finie, tout son système philosophique pourrait être réfuté[24]. Lorsqu'il dérive les lois de Snell-Descartes, il accepte la contradiction que la lumière se déplace instantanément, alors que son système philosophique affirme que plus dense est le médium, plus rapide est la lumière[35]. Pierre de Fermat, qui soutient que la vitesse de la lumière est finie, dérive les mêmes lois en utilisant l'argument opposé que la lumière voyage moins vite dans les médiums plus denses[36].
Premières tentatives de mesures

Le Soleil est la figure près de la lettre A. La Terre suit l'orbite qui passe par les points E, F, G, H, L et K. Jupiter est représenté par le petit cercle identifié par la lettre B, alors que l'orbite de la lune Io passe par les points C et D. La zone d'ombre solaire de Jupiter est représentée par le rectangle grisé.
Rømer a observé que la durée de l'occultation de Io changeait selon la position de la Terre. Il devait soit conclure que la période orbitale de Io changeait, soit que la vitesse de la lumière était finie.
En 1629, Isaac Beeckman propose une expérience où une personne observe l'éclair d'un coup de canon réfléchi sur un miroir à une distance d'environ 1 mile (1,6 km)[8]. En 1638, Galilée propose une autre expérience, qu'il aurait réalisée quelques années plus tôt, pour mesurer c en observant le délai entre l'exposition du hublot d'une lanterne allumée et de la détection de la lumière projetée à quelque distance de là. Il aurait été incapable de déterminer si c est infinie ou pas. Il conclut que si elle n'est pas infinie, elle doit être très grande[7],[8]. En 1667, l’Accademia del Cimento de Florence rapporte avoir effectué l'expérience de Galilée, avec des lanternes distantes d'environ 1 mile. Aucun délai n'est observé[10],[11],[note 3].
Ole Rømer est, en 1676, le premier à tenter de mesurer c. Connaissant la période orbitale de la lune Io de Jupiter, il détermine qu'elle raccourcit lorsque la Terre approche de Jupiter et qu'elle allonge lorsque la Terre s'éloigne de Jupiter. Il conclut que la lumière voyage à une vitesse finie ; il estime qu'elle prend 22 minutes à franchir le diamètre de l'orbite terrestre[37],[12]. Pour sa part, Christian Huygens combine cette durée avec une estimation du diamètre de l'orbite terrestre et calcule que c égale 220 000 km/s[13],[note 4].
Dans son livre Opticks de 1704, Isaac Newton rapporte les calculs de Rømer et affirme que la lumière franchit la distance séparant le Soleil de la Terre en « sept ou huit minutes »[trad 2],[38],[note 5]. En 1729, James Bradley découvre l'aberration stellaire[39]. En s'appuyant sur cet effet, il détermine que c égale 10 210 fois la vitesse orbitale de la Terre[note 6] ou, de façon équivalente, qu'il faut à la lumière 8 min 12 s pour franchir la distance Soleil-Terre[39].
Lien avec l'électromagnétisme
Au XIXe siècle, Hippolyte Fizeau développe une méthode pour déterminer c en effectuant des mesures terrestres du temps de vol de la lumière ; il rapporte la valeur de 315 000 km/s[40]. En 1856, Wilhelm Eduard Weber et Rudolf Kohlrausch, grâce aux décharges électriques d'une bouteille de Leyde, mesurent une unité de charge électromagnétique et une unité de charge électrostatique ; ils calculent le rapport des deux unités et obtiennent une vitesse proche de la valeur obtenue par Fizeau. L'année suivante, Gustav Kirchhoff calcule qu'un signal électrique voyage dans un fil sans résistance à cette même vitesse[41]. Au début des années 1860, James Clerk Maxwell démontre, dans le cadre de sa théorie de l'électromagnétisme, que les ondes électromagnétiques se propagent dans le vide[42],[43],[44] à une vitesse égale à celle calculée par Weber et Kohlrausch, tout en attirant l'attention sur la proximité numérique avec la vitesse de la lumière mesurée par Fizeau[45]. Pour lui, la lumière est une onde électromagnétique[46]. Améliorant la méthode de Fizeau, Léon Foucault obtient 298 000 km/s en 1862[14].
Éther luminifère

Aux XIXe siècle, les scientifiques pensent qu'un médium est nécessaire pour qu'un phénomène ondulatoire puisse se produire, peu importe que ce soit une vague ou une onde sonore par exemple. Puisque la lumière se propage dans le vide, il doit être rempli d'un médium qui sert à la propagation des ondes lumineuses. La Terre, qui se déplace dans ce médium immobile appelé « éther luminifère », est soumise à l'équivalent d'un vent[note 7],[47].
Reprenant cette hypothèse, des scientifiques du XIXe siècle pensent qu'il est possible de mesurer la vitesse de la Terre en détectant un changement dans la vitesse de la lumière. En effet, si la Terre s'éloigne ou se rapproche du Soleil par exemple, la vitesse de la lumière issue du Soleil change selon la loi de composition des vitesses[47].
Au début des années 1880, plusieurs expériences sont menées pour calculer la vitesse de la Terre[48]. La plus connue est l'expérience de Michelson–Morley de 1887[49]. Pendant cette expérience, la vitesse détectée est toujours plus petite que l'erreur d'observation[50],[51]. Des expériences menées au XXe siècle démontrent que l'erreur est inférieure à 6 nanomètres par seconde ; il faut donc conclure que la lumière se déplace à la même vitesse, peu importe la direction de propagation (elle est donc isotrope)[52]. À la suite de cette expérience, George FitzGerald et Hendrik Lorentz proposent de façon indépendante que les appareils utilisés se contractent dans le sens du mouvement, ce qui annulerait l'effet du vent d'éther. Lorentz indique de plus que le temps d'un système en mouvement, qu'il appelle « temps local », doit aussi être modifié par le même facteur, ce qui mène à la formulation des transformations de Lorentz. En se basant sur la théorie de l'éther de Lorentz, Henri Poincaré démontre en 1900 que ce temps local (une approximation d'ordre 2 du rapport v/c) est celui indiqué par les horloges qui se déplacent dans l'éther, qui sont synchronisées en faisant l'hypothèse que c est constante. En 1904, il spécule que c pourrait être l'ultime vitesse en dynamique, à la condition que toutes les hypothèses de la théorie de Lorentz soient validées. En 1905, il démontre, en se basant sur différentes expériences, que la théorie de l'éther de Lorentz explique complètement le principe de relativité[53],[54].
En 1905, le physicien Albert Einstein postule que la vitesse de la lumière dans le vide, telle que mesurée par des observateurs non accélérés, est indépendante du mouvement de la source et du mouvement des observateurs. En se basant à la fois sur cette invariance et le principe de relativité, il jette les bases de la relativité restreinte, où c est élevée au rang de constante fondamentale de l'Univers, constante qui apparaît dans des contextes où la lumière ne joue aucun rôle direct. Sa théorie rend caduque la notion d'éther luminifère (hypothèse que soutiennent encore Lorentz et Poincaré) et met de l'avant ce qui sera appelé l'« espace-temps », une façon de représenter l'espace et le temps comme deux notions inséparables[55],[56],[57].
Des mesures de plus en plus précises, redéfinitions du mètre et de la seconde
Dans la seconde moitié du XXe siècle, des progrès techniques permettent de préciser encore plus la valeur de la vitesse de la lumière. En 1950, Louis Essen détermine que c égale 299 792,5 ± 3,0 km/s en utilisant une cavité résonnante[18]. Cette valeur est adoptée par la 12e assemblée de l'Union radio-scientifique internationale en 1957. En 1960, le mètre est redéfini en fonction de la longueur d'onde d'une ligne spectrale particulière du krypton 86. En 1967, c'est au tour de la seconde d'être redéfinie selon la fréquence de transition hyperfine de l'état fondamental du césium 133[58].
En 1972, en utilisant des techniques d'interférométrie par laser et les nouvelles définitions, un groupe du National Bureau of Standards détermine que la vitesse de la lumière dans le vide est de 299 792 456,2 ± 1,1 m/s. Cette mesure est 100 fois plus précise que la plus précise des mesures précédentes. L'incertitude est surtout attribuable à la définition du mètre[note 8],[20]. D'autres expériences ayant déterminé la même valeur de c, la 15e Conférence générale des poids et mesures (CPGM), tenue en 1975, recommande d'utiliser la valeur de 299 792 458 m/s pour la vitesse de la lumière[61].
Définition de la vitesse de la lumière comme une constante explicite
En 1983, le 17e congrès de la CGPM conclut que, comparativement aux méthodes reconnues par les standards en vigueur, il est plus facile de reproduire certaines longueurs d'onde à partir de mesures de fréquences et d'une valeur connue de c. Le congrès retient la définition de 1967 pour la seconde, ce qui fait de la fréquence hyperfine du césium la base servant à définir la seconde et le mètre. Le congrès déclare que « le mètre est la longueur du trajet parcouru par la lumière dans le vide pendant l'intervalle temporel de 1299 792 458 seconde »[trad 4],[21]. En conséquence, la valeur de c est définie exactement égale à 299 792 458 m/s[62],[63],[64] et devient ainsi une constante définie dans le Système international d'unités (SI)[65]. La décision du congrès impose que la valeur du mètre dépende dorénavant de mesures plus précises de fréquences ou de longueurs d'ondes de la lumière, par exemple en mesurant plus précisément la longueur d'onde de la transition hyperfine du krypton 86 ou de toute autre source d'ondes électromagnétiques[66],[67].
En 2011, le CGPM déclare son intention de redéfinir les sept unités de base du SI en utilisant ce qu'il appelle « la formulation des constantes explicites »[trad 5], où chaque « unité est définie indirectement en spécifiant explicitement une valeur exacte pour une constante fondamentale bien connue »[trad 6], comme il a été fait pour c[68]. Une nouvelle définition du mètre, complètement équivalente, est proposée : « Le mètre, symbole m, est l’unité de longueur du SI. Il est défini en prenant la valeur numérique fixée de la vitesse de la lumière dans le vide, c, égale à 299 792 458 lorsqu’elle est exprimée en m/s, la seconde étant définie en fonction de ∆νCs. »[note 9]. Cette définition est inscrite dans le « SI révisé »[70].
Rôle fondamental en physique
Invariance
La vitesse à laquelle se déplace la lumière dans le vide est à la fois indépendante de la vitesse de la source et du référentiel inertiel de l'observateur[71],[72],[note 10]. Cette invariance a été postulée par Albert Einstein en 1905[73], après une étude de la théorie de l'électromagnétisme de James Clerk Maxwell et du manque de preuve de l'existence de l'éther luminifère[74]. Son hypothèse a été confirmée à maintes reprises par la suite[75],[note 11]. Il est seulement possible de vérifier expérimentalement que la vitesse d'un rayon de lumière effectuant un aller-retour (par exemple, d'une source à un miroir, et vice-versa) ne dépend pas du référentiel inertiel, parce qu'il est impossible de mesurer la vitesse de la lumière dans un seul sens (d'une source à un très lointain détecteur par exemple) sans avoir établi au préalable une convention pour synchroniser les horloges à la source et au détecteur. Toutefois, en adoptant la synchronisation d'Einstein, c dans un sens et c dans un aller-retour sont identiques par définition[76],[77].
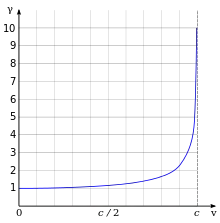
La relativité restreinte, fondée par Albert Einstein en 1905, explore plusieurs conséquences de l'invariance de c. Par exemple, c est la vitesse à laquelle toutes les particules sans masse et toutes les ondes électromagnétiques se propagent dans le vide[72],[71]. Cette théorie prédit des phénomènes contre-intuitifs, qui ont été vérifiés expérimentalement[78]. Parmi ceux-ci, il y a l'équivalence masse-énergie (exprimée par )[79], la contraction des longueurs[80] (les objets en mouvement sont plus courts dans le sens du mouvement)[note 12] et la dilatation du temps[83] (les horloges en mouvement avancent plus lentement). Le facteur de Lorentz, noté γ, permet de calculer la contraction de la longueur et la dilatation du temps d'un objet en mouvement[84] ; il est donné par la formule γ = , où v est la vitesse de l'objet et c, la vitesse de la lumière[85]. La valeur de γ est très proche de 1 aux vitesses beaucoup plus faibles que c, ce qui est le cas pour la plupart des vitesses observées dans la vie courante[85] — dans ces cas, les valeurs calculées par la relativité restreinte sont très proches de celles calculées par la relativité galiléenne. Il augmente sensiblement aux vitesses dites relativistes (donc, proches de c) et tend vers l'infini positif lorsque v est très proche de c[86]. Par exemple, le taux de contraction γ d'un objet en mouvement égale 2 lorsque sa vitesse relative atteint 86,6 % de c. Par ailleurs, un taux de dilation du temps γ = 10 apparaît lorsque v = 99,5 % c[note 13].
Les résultats de la relativité restreinte peuvent être résumés en regroupant l'espace et le temps dans une seule structure appelée « espace-temps », tout en exigeant que soit satisfaite l'invariance de Lorentz, dont la formulation mathématique comprend c[87] (elle permet de relier l'espace au temps puisque c comprend à la fois les unités de mesure de l'espace et du temps). L'invariance de Lorentz, une symétrie, est une hypothèse de base régulièrement mentionnée dans les théories physiques fondamentales modernes, telles l'électrodynamique quantique, la chromodynamique quantique, le modèle standard de la physique des particules et la relativité générale. En conséquence, c apparaît en beaucoup d'endroits en physique. Par exemple, la relativité générale prédit que c est aussi la vitesse de la gravité et des ondes gravitationnelles[88],[note 14]. Dans les référentiels non inertiels (des espaces-temps courbés par la gravité ou des référentiels accélérés), la vitesse de la lumière locale est constante et égale c. Elle peut être différente sur une trajectoire de longueur finie selon la façon dont sont définis les distances et les temps[90].
La plupart des scientifiques pense que les constantes fondamentales, telle que c, sont identiques peu importe l'espace-temps choisi. Elles seraient donc indépendantes du lieu et du temps où elles seraient calculées ou observées. Néanmoins, des scientifiques ont produit des théories où c serait différente selon l'époque cosmologique[91],[92]. Aucune preuve concluante qui permettrait de valider ces théories n'a été trouvée jusqu'en 2013, et la recherche se poursuit[93],[94].
Également, c est régulièrement jugée isotrope, c'est-à-dire qu'elle a la même valeur peu importe sa direction de propagation. Les observations d'ondes émises (1) par des noyaux atomiques plongés dans un champ magnétique variable[95] et (2) par des résonateurs optiques en rotation, imposent des limites strictes et très faibles sur l'imprécision d'une anisotropie en fonction de l'angle d'observation[96],[97].
Vitesse limite
Selon la relativité restreinte, l'énergie d'un objet ayant une masse au repos m et une vitesse v est donnée par γmc2, où γ est le facteur de Lorentz (qui comprend le terme v). Quand v est nulle, γ égale un, ce qui mène à la « fameuse équation »[1] (équivalence masse-énergie). γ tend vers l'infini positif lorsque v approche de c et il faudrait une énergie encore plus grande (jusqu'à une valeur infinie) pour accélérer encore plus un objet pesant pour lui faire atteindre c. La vitesse de la lumière dans le vide est dont l'ultime limite pour les objets en mouvement dotés d'une masse au repos positive. Les photons individuels ne peuvent voyager plus vite que cette vitesse[98],[99],[100]. Ces hypothèses ont été confimées expérimentalement[101].
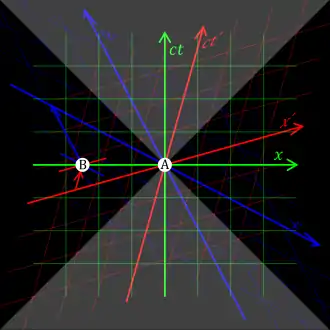
Plus généralement, il est impossible aux signaux ou à l'énergie de voyager plus vite que c. Un argument en faveur de cette position provient de la relativité de la simultanéité, l'une des conséquences de la relativité restreinte. Si la distance spatiale des évènements A et B est plus grande que l'intervalle de temps entre les deux multiplié par c, alors il existe des référentiels où A précède B, d'autres où B précède A et d'autres où les deux sont simultanés. En conséquence, si quelque chose voyageait plus vite que c relativement à un référentiel inertiel, il reculerait dans le temps relativement à un autre référentiel et la causalité serait violée[note 15],[103].
Dit autrement, un effet serait observé avant sa cause. Ce phénomène, qui n'a jamais été observé[77], mènerait par exemple à l'existence d'un antitéléphone tachyonique, c'est-à-dire un hypothétique appareil qui pourrait être utilisé pour envoyer un signal dans son passé[104]. Albert Einstein en 1907[105],[106] présente une expérience de pensée où des signaux supraluminiques pourraient provoquer un paradoxe de causalité. En 1910, Arnold Sommerfeld et Einstein le décrivent comme un moyen de « télégraphier dans le passé »[trad 7],[107]. La même expérience de pensée a été décrite par Richard Tolman en 1917[108] ; des scientifiques peuvent faire allusion à cet appareil en mentionnant le « paradoxe de Tolman ». Plus tard, il a été nommé « antitéléphone tachyonique »[trad 8] par Gregory Benford et al[109].
Dans les domaines de la physique où c apparaît régulièrement, comme la relativité restreinte et la relativité générale, il est courant d'utiliser des système d'unités naturelles de mesures ou des systèmes d'unités géométriques dans lesquelles c = 1[110],[111],[note 16].
Observations et expériences de vitesses supraluminiques
Certaines observations laissent penser, à tort, que la matière, l'énergie ou des signaux transportant des informations se déplacent à une vitesse supérieure à c. Par exemple, tel que discuté dans la section Dans un médium ci-dessous, les vitesses de plusieurs caractéristiques d'ondes peuvent excéder c. Par exemple, les vitesses de phase des rayons X, lorsqu'ils traversent la plupart des verres, dépassent régulièrement c[112], mais aucune vitesse de phase n'influe sur la vitesse à laquelle les ondes transportent des informations[113].
Si un faisceau laser balaie rapidement un objet distant, la vitesse de la tache lumineuse peut se déplacer plus rapidement que c. Il y a un délai entre le moment où le faisceau initial quitte le laser et le moment où la réflexion du faisceau parvient à un observateur. Les seuls objets qui se déplacent sont le laser et le faisceau, la vitesse de ce dernier atteignant au plus c avant qu'il n'atteigne le site de réflexion. De la même façon, une ombre sur un objet lointain peut se déplacer plus rapidement que c, mais l'absence de lumière se déplace à c[114]. Dans ces deux cas, ni la matière, ni l'énergie et ni l'information ne voyagent plus rapidement que la lumière[115].
La vitesse de changement de la distance entre deux objets observée dans un référentiel distinct de ceux des deux objets peut dépasser c. Encore une fois, cela ne représente pas la vitesse d'un objet dans le même référentiel inertiel[115].
Quelques effets quantiques semblent être transmis instantanément et seraient dont plus rapide que c, comme par exemple dans le paradoxe EPR. Un exemple met en jeu les états quantiques de deux particules intriquées. Tant qu'elles ne sont pas observées, elles sont superposées dans deux états quantiques. Si les deux sont séparées et que l'état de l'une est observé, alors l'état de l'autre est déterminé instantanément. Néanmoins, il est impossible de vérifier dans quel état quantique se trouve la première particule sans l'observer au préalable ; donc, aucune information ne peut être transmise de cette façon[115],[116].
L'effet Hartman prédit l'existence de vitesses supérieures à c : sous certaines conditions, le temps nécessaire à une particule virtuelle de franchir une barrière grâce à un tunnel quantique est constant, peu importe l'épaisseur de la barrière[117],[118]. Si la barrière est suffisamment mince, la particule virtuelle franchit la barrière à une vitesse supérieure à c. Encore une fois, aucune information ne peut être transmise ainsi[119].
Des vitesses supraluminiques sont observées dans certains phénomènes astronomiques[120], tels que les jets relativistes de radiogalaxies et de quasars. Ces jets ne se déplacent pas à une vitesse supérieure à celle de la lumière : c'est la conséquence de la projection géométrique du mouvement apparent de ces objets qui voyagent à une vitesse proche de c et qui sont observés sous un petit angle de la ligne de mire. Ces objets s'éloignent de la Terre à une vitesse relativiste ; le temps d'observation de chaque rayon successif est plus grand que le précédent[121].
Selon les modèles inflationnistes de l'Univers, le plus loin se trouve une galaxie, le plus rapidement elle s'éloigne[122]. Cette récession n'est pas la conséquence du mouvement dans l'espace, mais plutôt de l'expansion de l'Univers[123]. Par exemple, les galaxies distantes de la Terre semblent s'en éloigner à des vitesses proportionnelles à leur distance[122]. Au-delà du volume de Hubble, la vitesse d'éloignement est plus grande que c[124].
Propagation de la lumière
En physique classique, la lumière est considérée comme une onde électromagnétique. Dans ce cadre, le comportement du champ électromagnétique est décrit par les équations de Maxwell qui prédisent que c, vitesse à laquelle les ondes électromagnétiques (dont la lumière visible) se propagent dans le vide, est fonction de la capacité du vide et de l'inductance du vide. Ces deux caractéristiques, appelées respectivement la permittivité du vide () et la perméabilité du vide (), sont reliées à la vitesse de la lumière dans le vide (c) par l'équation[125] :
En mécanique quantique, approche plus moderne, le champ électromagnétique est décrit par l'électrodynamique quantique (QED). La lumière y est décrite comme une excitation fondamentale (ou quanta) du champ électromagnétique ; elle est alors composée de photons, qui sont également des particules sans masse[126],[127].
Des extensions de QED où le photon est doté d'une masse ont été étudiées. Dans ces cadres théoriques, la vitesse du photon dépendrait de sa fréquence et l'invariant c de la relativité restreinte serait alors la limite ultime de la vitesse de la lumière dans le vide[90]. Toutefois, aucune variation de la vitesse de la lumière en fonction de la fréquence n'a été observée dans des conditions de laboratoire rigoureuses[128],[129],[130], lesquelles ont imposé des limites strictes sur la masse du photon. La limite calculée dépend du modèle utilisé : si le photon massif est décrit selon l'approche de Proca par exemple[131], alors la limite supérieure expérimentale pour sa masse est de 10−57 gramme[132].
Une autre raison qui militerait en faveur de la vitesse de la lumière en fonction de sa fréquence serait l'impossibilité d'appliquer la relativité restreinte à de très petites échelles arbitraires, tel que prédit par quelques théories s'appuyant sur la gravité quantique. En 2009, l'observation de sursauts gamma provenant du système stellaire GRB 090510 n'a pas démontré que la vitesse du photon dépend de son énergie, ce qui impose des limites strictes aux modèles de quantification de l'espace-temps qui s'appuient sur l'idée que cette vitesse est influencée par l'énergie du photon lorsque les énergies sont proches de l'échelle de Planck[133].
Dans un médium
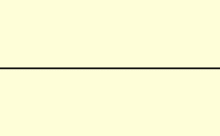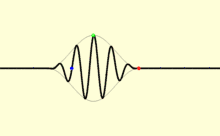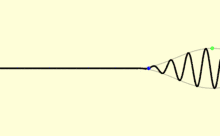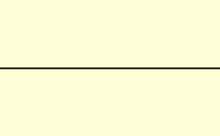
Au moins huit vitesses différentes peuvent être utilisées pour caractériser la propagation de la lumière, à savoir : (1) la vitesse de phase, (2) la vitesse de groupe, (3) la vitesse d'énergie, (4) la vitesse de signal, (5) la constante de vitesse relativiste, (6) la vitesse de rapport d'unités, (7) la centrovitesse et (8) la vitesse de corrélation[134],[135]. Dans le vide, toutes ces vitesses sont égales à c, alors que dans un autre milieu, seule la vitesse du front d'onde conserve cette valeur. Par ailleurs, pour des fréquences différentes, les vitesses sont différentes. Dans une onde plane, chaque crête et chaque creux se propage à vp, la vitesse de phase. Un signal physique qui a une portée finie (une impulsion de lumière) voyage à une vitesse différente. La plus grande partie d'une impulsion voyage à vg, la vitesse de groupe, alors que l'autre partie voyage à vf, la vitesse de front.
La vitesse de phase est importante pour déterminer comment une onde lumineuse se propage dans un matériau ou d'un matériau à un autre. Régulièrement, cette information est décrite par l'indice de réfraction qui est défini par le rapport de c à la vitesse de phase vp du matériel (plus grand est l'indice, plus faible est la vitesse de l'onde). L'indice de réfraction dépend de plusieurs facteurs, dont la fréquence de la lumière, son intensité, sa polarisation et sa direction de propagation. Néanmoins, dans plusieurs cas, il est traité comme une quantité invariable[136].
L'indice de réfraction de l'air est d'environ 1,0003[136]. Des médias plus denses, comme l'eau[137], le verre[138] et le diamant[139], présentent des indices de réfraction d'environ 1,3, 1,5 et 2,4 pour la lumière visible. Dans des matériaux exotiques, tel le condensat de Bose-Einstein maintenu à une température très proche du zéro absolu, la lumière peut se déplacer à quelques mètres par seconde. Dans ces cas, la durée prise par les atomes pour absorber puis émettre la lumière est significativement plus longue que si le processus d'absorption-émission avait été réalisé à 0 °C par exemple. Deux équipes de physiciens ont affirmé avoir complètement arrêté la lumière en la faisant passer dans un condensat de Bose-Einstein de rubidium. L'énergie de la lumière est stockée dans les atomes (qui deviennent ainsi excités), puis émise plus tard sous forme lumineuse si les atomes sont illuminés par un faisceau laser. Le comportement absorption-émission retardée est en général vrai au niveau microscopique pour tous les médiums transparents qui « ralentissent » la lumière[140].
Dans les matériaux transparents, l'indice de réfraction est habituellement plus grand que 1, ce qui signifie que la vitesse de phase est plus petite que c. Dans certains matériaux, l'indice de réfaction peut être plus faible que 1 à certaines fréquences lumineuses ; dans quelques matériaux exotiques, l'indice peut être négatif[141]. L'exigence que la causalité ne soit pas violée implique que les parties réelle et imaginaire de la permittivité d'un matériau, qui correspondent respectivement à l'indice de réfraction et au coefficient d'extinction, soient reliées par les relations de Kramers-Kronig[142]. En pratique, dans un matériau qui présente un indice de réfraction inférieur à 1, l'absorption de l'onde lumineuse est si rapide qu'aucun signal ne peut être transmis plus vite que c.
Une impulsion lumineuse avec des vitesses de groupe (vg) et de phase (vp) différentes (qui survient lorsque la vitesse de phase change selon la fréquence des ondes de l'impulsion) s'étale avec le temps, un processus appelé dispersion. Quelque matériaux présentent une vitesse de groupe très faible (ou même nulle) pour les ondes lumineuses, un phénomène appelé lumière lente[143],[144],[145],[146]. L'opposé, des vitesses de groupe supérieures à c, a aussi été mis en évidence par des expériences[147]. En théorie, la vitesse de groupe pourrait être infinie ou négative, avec des impulsions voyageant instantanément ou à reculons dans le temps[148]. Néanmoins, toutes ces possibilités ne permettent pas de transmettre de l'information à une vitesse supérieure à c. Il est en effet impossible de transmettre de l'information avec une impulsion lumineuse plus rapide que la vitesse de la première partie d'une onde, la vitesse de front. Sous certaines conditions, elle est toujours égale à c[148].

Une particule peut voyager plus rapidement que la vitesse de phase de la lumière dans un médium (cette vitesse étant toujours plus faible que c). Quand une particule chargée se propage ainsi dans un matériau diélectrique, l'équivalent électromagnétique d'une onde de choc se produit, c'est l'effet Tcherenkov[149].
Dans un milieu biréfringent, la vitesse de la lumière dépend de son plan de polarisation, phénomène utilisé dans de très nombreux domaines, que ce soit la microscopie ou la fabrication de lunettes de soleil[150].
Conséquences pratiques de la finitude de c
La vitesse de la lumière est importante dans le domaine des télécommunications : un aller simple et un aller-retour ne sont pas instantanés. Cette constatation s'applique à tous les objets connus dans l'Univers, que ce soit des atomes ou de lointaines galaxies. Quelques techniques s'appuient sur la finitude de c, notamment en métrologie.
À petites échelles

Dans les superordinateurs, la vitesse de la lumière impose une limite à la vitesse de transmission de l'information entre les processeurs. Si un processeur opère à 1 gigahertz, un signal ne peut parcourir qu'une distance d'environ 30 cm par cycle. Pour une vitesse maximale de traitement, les processeurs doivent donc être logés les uns près des autres pour minimiser la latence de la communication ; cette contrainte peut réduire l'efficacité du refroidissement. Si la cadence de l'horloge du processeur augmente, la vitesse de la lumière devient alors une contrainte ferme lors de la conception d'une puce électronique[151],[152].
Mesures de distances
Les radars mesurent la distance en calculant le temps pris par un signal pour faire l'aller-retour entre une cible réfléchissante et l'instrument de lecture[153] : la distance entre les deux est proportionnelle au temps multiplé par c. Un récepteur GPS calcule de même, mais en s'appuyant sur les signaux émis par plusieurs satellites GPS qui émettent en continu. Puisque la lumière parcourt environ 300 000 kilomètres en une seconde, les détecteurs embarqués et les calculs doivent être d'une grande précision[154]. Le Lunar Laser Ranging Experiment, l'astronomie radar et le Deep Space Network calculent respectivement les distances à la Lune[155], aux planètes[156] et aux vaisseaux spatiaux[157] en mesurant les temps d'aller-retour d'ondes électromagnétiques.
Longs parcours sur la Terre
Puisque la circonférence équatoriale de la Terre mesure environ 40 075 km[note 17] et que c est d'environ 300 000 km/s, la durée minimale théorique pour qu'une information atteigne le point opposé de la Terre en circulant à sa surface seulement est d'environ 67 millisecondes. Quand la lumière circule dans une fibre optique autour du globe, le temps de transit est plus long, entre autres parce que la vitesse de la lumière y est diminuée d'environ 35 %, selon l'indice de réfraction n du matériau de la fibre[note 18]. De plus, le signal lumineux doit être régénéré régulièrement ou encore converti en signal électronique puis optique ; ces opérations durent plus longtemps que le temps pris par la lumière pour parcourir en ligne droite la distance entre l'entrée et la sortie de l'un de ces appareils[159].
Voyages spatiaux et astronomie
Les communications entre la Terre et un vaisseau spatial ne sont pas instantanées. Plus les deux sont éloignés, plus le délai entre l'émission et la réception d'un signal est grand. Ce délai est devenu apparent lors des communications entre le Mission Control Center de la NASA et la capsule d'Apollo 8 qui orbitait autour de la Lune (en décembre 1968) : pour chaque question, le premier devait attendre au moins 3 secondes avant de recevoir une réponse[161]. Le délai de communication entre la Terre et Mars varie entre 5 et 20 minutes selon leur position relative[162]. En conséquence, si un robot sur Mars éprouve un problème, son contrôleur humain ne le sait pas avant 5 minutes et peut-être même après 20 minutes. Il faudrait encore au moins de 5 à 20 minutes pour inciter le robot à effectuer une manœuvre corrective.
La lumière qui provient d'objets astronomiques lointains prend encore plus de temps pour atteindre la Terre. Par exemple, l'un des objets célestes de l'image Hubble Ultra Deep Field a émis de la lumière qui a parcouru l'Univers pendant 13 milliards d'années avant d'être détectée par le télescope spatial Hubble[163],[164]. Cette image, construite aujourd'hui, capture l'état de cette lointaine galaxie voici 13 milliards d'années, quand l'Univers était âgé d'un milliard d'années[163].
Les distances astronomiques sont parfois exprimées en années-lumière, surtout dans les ouvrages de vulgarisation et dans les médias de masse[165]. Une année-lumière est la distance parcourue par la lumière dans le vide pendant une année, c'est-à-dire environ 9 461 milliards de kilomètres ou 0,306 6 parsec[166]. Proxima Centauri, l'étoile la plus près de la Terre après le Soleil, se trouve à environ 4,2 années-lumière[167].
Transactions à haute fréquence
La vitesse de la lumière est d'une certaine importance dans les transactions à haute fréquence, où des courtiers tentent de gagner de petits avantages financiers en effectuant des transactions une fraction de seconde avant leurs compétiteurs. Par exemple, des courtiers préfèrent utiliser des systèmes de communication à micro-ondes, parce que ces ondes circulent presque à c alors que la lumière dans les fibres optiques voyagent de 30 à 40 % moins rapidement[168],[169].
Mesures
On peut mesurer c de plusieurs façons. Par exemple, en observant la façon dont les ondes lumineuses se propagent grâce à des instruments astronomiques. On peut la mesurer en fonction de constantes connues, telles la permittivité du vide () et la perméabilité du vide (). On peut également calculer cette valeur en connaissant la longueur d'onde et la fréquence d'une onde lumineuse, puisque leur produit égale c.
Depuis 1983, le Système international d'unités (SI) fixe la vitesse de la lumière à exactement 299 792 458 m/s[170],[171],[65]. En tant que constante dotée d'unités de mesure, la valeur numérique de c diffère selon le système d'unités[note 1].
La question de la constance de la vitesse de la lumière dans le vide ne peut être tranchée puisqu'il est théoriquement possible que les photons aient une masse non nulle : les mesures ne peuvent que plafonner cette masse hypothétique et non prouver qu'elle est rigoureusement nulle. Toutefois, même s'il était avéré que les photons ont une masse, cela ne remettrait pas en cause le principe de la constante c, mais donnerait plutôt une limite de précision de son observabilité dans les modèles de référence[172].
Mesures astronomiques
Le milieu interstellaire est un lieu pertinent pour mesurer la vitesse de la lumière à cause de sa grandeur et de l'absence quasi totale d'obstacles sur de grandes distances. Historiquement, les scientifiques ont mesuré le temps de parcours de la lumière en fonction d'une distance connue dans le Système solaire, tel le diamètre de l'orbite terrestre.
Ole Christensen Rømer effectue en 1676 une mesure astronomique qui lui permet de prédire que la vitesse de la lumière est finie[37],[12].
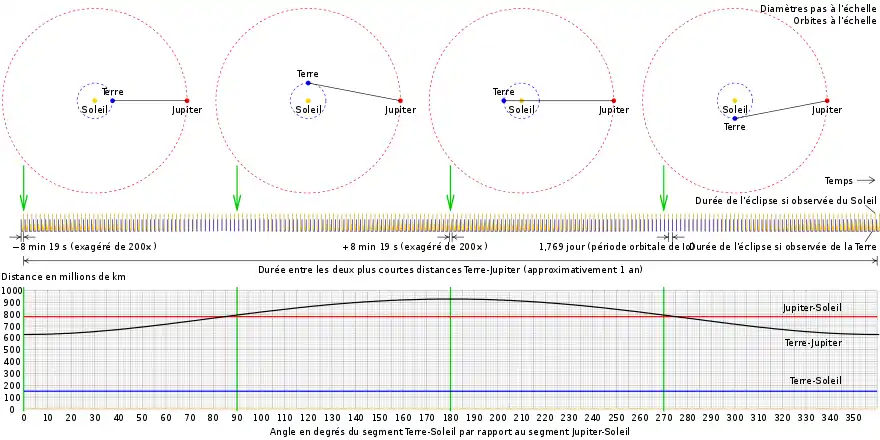
Pourtant, Rømer observe que les débuts et les fins des éclipses d'Io ne correspondent pas aux heures calculées. Puisque la période orbitale de Io est invariable et que l'observation de cette lune indique que cette période varie, il faut conclure que la vitesse de la lumière est finie.
Le Soleil, la Terre et Jupiter forment un triangle dont l'angle Terre-Soleil-Jupiter peut être mesuré. De plus, les rayons des orbites terrestre et jovienne sont connus. On peut donc calculer la distance Terre-Jupiter au 120e jour de l'orbite terrestre par exemple par la loi des cosinus. Une fois cette distance connue ainsi que la différence entre le temps calculé et le temps d'observation, on peut déterminer la vitesse de la lumière, soit le rapport distance au temps.
Entre 1671 et 1673, Rømer observe une variation dans la durée de l'orbite de la lune Io de Jupiter[173] et déduit que la lumière prend de 10 à 11 minutes pour parcourir le diamètre de l'orbite terrestre[174],[175]. C'est néanmoins Christian Huygens qui calcule la vitesse de la lumière à partir des observations astronomiques de Rømer et de Jean-Dominique Cassini : 230 000 km/s, probablement parce que Rømer doutait de sa capacité à pouvoir calculer la valeur numérique d'une telle grandeur et que Cassini rejetait l'hypothèse de Rømer[176].
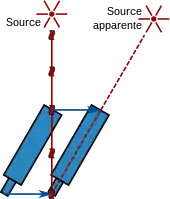
Une autre méthode pour mesurer c est d'utiliser l'aberration de la lumière, découverte et expliquée par James Bradley au XVIIIe siècle[39]. Cet effet s'explique par l'addition vectorielle de la vitesse de la lumière qui provient d'une source lointaine (comme une étoile) et la vitesse du télescope (voyez les explications du diagramme à la droite). Un observateur mobile voit un rayon de lumière d'une direction légèrement différente et, en conséquence, observe la source à une position décalée par rapport à sa position calculée. Cet effet est la source du mouvement apparent des étoiles dans le ciel puisque la direction de la vitesse de la Terre change continuellement (elle orbite autour du Soleil et tourne sur elle-même). En se basant sur la différence angulaire de la position des étoiles (20,5 secondes d'arc)[177], il est possible de déterminer c en fonction de la vitesse de la Terre autour du Soleil connaissant la durée d'une orbite terrestre complète. En 1729, Bradley détermine que c est 10 210 fois plus rapide que la vitesse orbitale de la Terre[note 19]. De façon équivalente, il faut 8 min 12 s pour que la lumière parcourt la distance Soleil-Terre[39].
Unité astronomique
Une unité astronomique (UA) est à peu près la distance moyenne entre la Terre et le Soleil. En 2012, elle a été fixée à exactement 149 597 870 700 m[178],[179]. Auparavant, elle n'était pas définie selon les unités du Système international d'unités, mais selon la force gravitationnelle exercée par le Soleil dans un référentiel de mécanique classique[note 20]. La définition moderne fixe la valeur de l'UA comme multiple de c[178].
Auparavant, l'inverse de c exprimé en secondes par UA était mesuré en comparant le temps pour un signal radio à atteindre différents vaisseaux spatiaux dans le Système solaire, leur position étant calculée en fonction des effets gravitationnels du Soleil et de planètes. En calculant une moyenne de plusieurs mesures, une valeur du temps lumière par unité de distance s'obtient par meilleur ajustement. Par exemple, en 2009, la meilleure estimation, approuvée par l'Union astronomique internationale (UAI), est de[181],[182],[183] :
- temps lumière par unité de distance :
L'incertitude relative est de 0,02 parties par milliard (2 × 10−11), équivalente à l'incertitude de la mesure terrestre d'une distance par interférométrie[184]. Puisque le mètre est défini comme la distance parcourue par la lumière en un certain intervalle de temps, la mesure du temps de parcours selon la définition précédente peut aussi être interprétée comme la longueur de l'UA (ancienne définition) en mètres[note 21].
Temps de vol

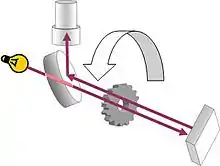
Une méthode pour déterminer c est de mesurer le temps pour un faisceau lumineux d'atteindre un lointain miroir et d'en revenir, méthode qu'utilise Hippolyte Fizeau en 1849[186],[187]. Le montage de Fizeau consiste en un faisceau de lumière dirigé vers un miroir à environ 8 km de la source et qui tombe sur les dents d'une roue dentelée en rotation. Lorsque cette roue atteint une certaine vitesse de rotation, le faisceau passe entre une paire de dents, est réfléchi puis passe entre la paire de dents suivante. Connaissant la distante entre la roue et le miroir, la distance entre deux dents et la vitesse de rotation, la vitesse de la lumière peut être calculée[14].
Léon Foucault préfère utiliser un miroir rotatif. Dans son expérience, réalisée en 1850, un faisceau de lumière tombe sur le miroir rotatif. Pendant que le faisceau se dirige vers le miroir fixe, puis est réfléchi, le miroir rotatif continue de tourner et le faisceau est réfléchi sur ce miroir rotatif à un angle différent de celui au début de son trajet. Connaissant la différence d'angle, la vitesse de rotation du miroir rotatif et la distance au miroir fixe, il est possible de calculer c[188],[189].
Au XXIe siècle, en utilisant un oscilloscope plus précis que la nanoseconde, c peut être déterminée en mesurant le temps pris par l'impulsion lumineuse d'un laser (ou d'une DEL) réfléchie par un miroir. La valeur obtenue est moins précise, de l'ordre de 1 %, que celles obtenues par un laboratoire proprement doté, mais elle a l'avantage de pouvoir être reproduite dans un laboratoire universitaire ordinaire[190],[191],[192].
En , la collaboration de physiciens travaillant sur l'expérience OPERA annonce que le temps de vol mesuré de neutrinos produits au CERN est inférieur de 60,7 ns à celui attendu pour des particules se déplaçant à la vitesse de la lumière[193],[194]. Le , la collaboration annonce que l'anomalie est en fait liée à une erreur de mesure due au branchement défectueux d’un câble de synchronisation optique des horloges atomiques, et que la vitesse mesurée des neutrinos est compatible avec celle de la lumière[195].
Constantes électromagnétiques
Une façon d'obtenir la valeur de c sans s'appuyer sur des mesures en lien avec la propagation d'ondes électromagnétiques, est d'utiliser la relation entre c, la permittivité du vide () et la perméabilité du vide () tel que démontré par Maxwell : [196],[197]. La permittivité peut être déterminée en mesurant la capacité électrique et les dimensions d'un condensateur, alors que la perméabilité est fixée à exactement 4π × 10−7 H/m à la suite de la définition de l'ampère. Rosa et Dorsey empruntent cette voie en 1907 et calculent 299 710 ± 22 km/s[15],[16].
Cavité résonnante
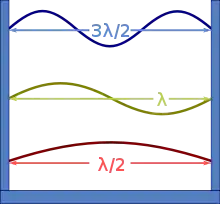
c se calcule par la relation [198]. Donc, c peut être établie si l'on mesure de façon indépendante la fréquence () et la longueur d'onde () d'une onde électromagnétique dans le vide.
Une autre façon de faire est de mesurer la fréquence de résonance dans une cavité résonnante. Si les dimensions de la cavité sont connues, on peut alors trouver la longueur d'onde. En 1946, Louis Essen et A. C. Gordon-Smith établissent plusieurs modes normaux des micro-ondes dans une cavité résonnante dont les dimensions sont connues avec une incertitude de ± 0,8 μm grâce à des mesures par interférométrie[15]. Puisque les longueurs d'onde des modes normaux sont connues grâce à l'électromagnétisme, la valeur de c peut être calculée pour plusieurs fréquences[15],[199]. Le résultat d'Essen–Gordon-Smith, 299 792 ± 9 km/s, est significativement plus précis que ceux obtenus par des méthodes optiques[15]. En 1950, Essen affirme, après avoir mené une suite d'expériences, avoir obtenu 299 792,5 ± 3,0 km/s pour c[18].
Une démonstration maison de cette technique peut se faire avec un four à micro-ondes et une substance fusible, telles que des guimauves ou de la margarine. Si la table pivotante est retirée de façon que l'aliment reste immobile, le four va cuire plus rapidement aux anti-nœuds (les points où l'amplitude de l'onde est la plus grande) ; donc, aux points où l'aliment fond le plus rapidement. La distance entre deux points est la moitié de la longueur d'onde des micro-ondes ; en mesurant cette distance et en multipliant par la fréquence des micro-ondes (inscrite sur la plaque signalétique du four, habituellement 2 450 MHz), la valeur de c peut être calculée « souvent avec une erreur inférieure à 5 % »[trad 9],[200],[201].
Interférométrie
Un faisceau de lumière cohérente (par exemple un laser), d'une fréquence connue (), est divisé en deux. Chaque partie suit un trajet différent, puis elles sont recombinées. En modifiant et mesurant avec précision la longueur d'un trajet tout en observant le motif d'interférence, la longueur d'onde () peut être déterminée. La vitesse de la lumière est donnée par [202].
la longueur d'onde d'une onde électromagnétique, puis c.
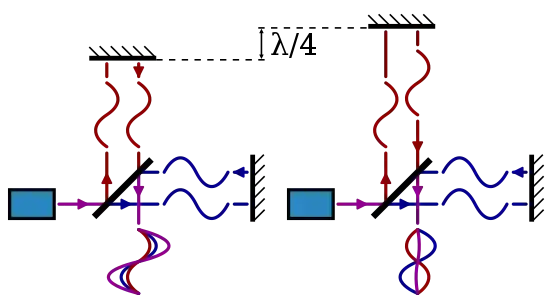
Dans la moitié gauche, un faisceau de lumière, de fréquence connue (), est issu de la source cohérente. Il est en partie réfléchi vers le haut, en partie transmis à travers le miroir semi-transparent. La partie qui monte est ensuite réfléchie vers le bas par le miroir horizontal. Pour sa part, la partie de faisceau qui a traversé le miroir est réfléchie par le miroir vertical. Si la distance entre le bas du miroir oblique et le miroir horizontal est un multiple de la longueur d'onde (), alors les deux parties, qui sont des ondes, formeront une interférence constructive (la courbe rose dans le motif en bas à la gauche).
Dans la moitié droite, un faisceau lumineux subit les mêmes transformations, mais la distance entre le bas du miroir oblique et le miroir horizontal est un multiple de plus . Les deux parties, toujours des ondes, formeront une interférence destructive (la courbe rose aplatie dans le motif en bas à la droite).
Lorsqu'il y a interférence constructive, l'observateur est illuminé par le faisceau recombiné. S'il y a interférence destructive, il ne voit que du noir.
Donc, en ajustant la longueur du trajet d'un faisceau lumineux tout en observant les motifs d'interférence, peut être déterminée.Avant la démocratisation des lasers, les sources d'ondes radio cohérentes ont servi à déterminer c par interférométrie[19]. Toutefois, la détermination de la longueur d'onde par interférométrie devient de moins en moins précise au fur et à mesure que la longueur d'onde augmente. Dans la pratique, les expériences perdent beaucoup de précision lorsque les longueurs d'onde dépassent 4 mm. La précision peut être augmentée en utilisant de la lumière de plus courte longueur d'onde, mais il devient alors difficile de mesurer directement sa fréquence. Une voie de contournement est de commencer avec un faisceau de faible fréquence pour lequel celle-ci peut être mesurée. Ensuite, synthétiser des ondes de plus grandes fréquences qui peuvent être liées au faisceau de départ. Un laser peut ensuite être syntonisé sur cette fréquence ; sa longueur d'onde est alors mesurée par interférométrie[203]. Cette technique, mise au point par une équipe du National Bureau of Standards, a été utilisée en 1972 pour mesurer la vitesse de la lumière dans le vide à une précision relative de 3,5 × 10−9[203],[20].
Notes et références
(en) Cet article est partiellement ou en totalité issu de la page de Wikipédia en anglais intitulée « Speed of light » (voir la liste des auteurs).
Citations originales
- (en) « light is due to the presence of something, but it is not a movement »
- (en) « seven or eight minutes »
- (en) « The metre is the length equal to 1 650 763,73 wavelengths in vacuum of the radiation corresponding to the transition between the levels 2p10 and 5d5 of the krypton 86 atom »
- (en) « the length of the path travelled by light in vacuum during a time interval of 1299 792 458 of a second »
- (en) « the explicit-constant formulation »
- (en) « unit is defined indirectly by specifying explicitly an exact value for a well-recognized fundamental constant »
- (en) « to telegraph into the past »
- (en) « tachyonic antitelephone »
- (en) « often with less than 5% error »
Notes
- La vitesse de la lumière dans le système anglo-saxon et dans le système américain est basé sur le pouce ayant la valeur exacte de 2,54 cm et elle égale donc :
- 299 792 458 m/s × 100 cmm × 12,54 pocm,
- Galilée rapporte que les lanternes se trouvaient à une courte distance, moins de 1,5 km (1 mile). En supposant que cette distance soit vraie, et qu'« au moins un trentième de seconde est l'intervalle minimum de temps pour la détection par un œil nu (« about a thirtieth of a second is the minimum time interval distinguishable by the unaided eye »), Boyer 1941 avance que l'expérience de Galilée ne pouvait que donner une limite basse d'environ 100 km/s pour la vitesse de la lumière.
- Pour cette distance, le délai serait d'environ 11 microsecondes.
- C'est-à-dire 26 % de moins que la valeur moderne.
- La valeur avancée au XXIe siècle est 8 min 19 s.
- Au XXIe siècle, c'est 10 066 fois.
- Situation analogue au déplacement d'un corps physique dans l'atmosphère terrestre. Lorsque nous marchons, on perçoit très peu ou pas la résistance de l'air, alors que si nous sommes dans un véhicule à haute vitesse, la résistance de l'air est perceptible.
- Entre 1960 et 1983, le mètre est défini ainsi : « Le mètre est la longueur égale à 1 650 763,73 longueurs d'onde dans le vide de la radiation qui correspond à la transition entre les niveaux 2p10 et 5d5 de l'atome de krypton 86 »[trad 3],[59]. Dans les années 1970, des scientifiques découvrent que la raie du spectre lumineux n'est pas symétrique, ce qui augmente l'imprécision sur la largeur de la raie lorsqu'elle est calculée en se basant sur l'interférométrie[60].
- La seconde est alors définie par la durée de 9 192 631 770 cycles de la radiation émise lors de la transition d'un électron entre deux niveaux d'énergie précis de l'atome de césium 133[69].
- Néanmoins, à cause de l'effet Doppler, la fréquence de la lumière dépend du mouvement de la source par rapport à un observateur.
- Voyez par exemple l'expérience de Michelson–Morley et l'expérience de Kennedy–Thorndike.
- Pour les objets en mouvement, leur longueur est plus courte dans le sens du mouvement et ils sont aussi observés à la fois pivotés et déformés. C'est la rotation de Terrell, qui est la conséquence des temps que prennent les rayons lumineux des différentes parties d'un objet à atteindre un observateur[81],[82].
- En effet,
- si v = 86,6 % c, alors γ = = 1,999824
- si v = 99,5 % c, alors γ = = 10,01
- En 2008, l'interprétation d'observations de systèmes binaires utilisés pour déterminer la vitesse de la gravité est mise en doute par quelques auteurs[89].
- Des scientifiques pensent que l'effet Scharnhorst permet à des signaux de voyager un peu plus rapidement que la lumière dans le vide, mais les conditions requises pour observer de tels signaux interdisent d'utiliser cet effet pour violer la causalité[102].
- De cette façon, c n'apparaît pas explicitement parce que la multiplication ou la division par 1 ne modifie pas le résultat.
- La Terre est une boule presque parfaite. Le rayon moyen de la Terre est de 6 378,136 6 km selon Luzum et al, 2011, p. 296. En appliquant la formule C = 2 π r, qui permet de trouver la circonférence d'une boule, on trouve C = 40 075 km.
- Dans les fibres optiques, l'indice de réfraction se situe le plus souvent entre 1,518 et 1,538[158].
- La science moderne l'établit à 10 066 fois plus rapide.
- L'unité astronomique a été définie comme le rayon d'une orbite newtonienne circulaire non perturbée autour du Soleil d'une particule dotée d'une masse infinitésimale se déplaçant à une fréquence angulaire de 0,017 202 098 95 radian par jour (environ 1⁄365,256 898 d'une révolution terrestre)[180].
- Néanmoins, à cette précision, les effets de la relativité générale doivent être pris en compte lors de l'interprétation de la longueur. Le mètre est considéré comme une unité de longueur propre, alors que l'UA est habituellement utilisée comme une unité de la longueur observée dans un référentiel donné. Les valeurs données ici suivent cette deuxième convention, et sont compatibles avec le temps dynamique barycentrique (TDB)[182].
Références
- (en) David Bodanis, E=mc2: A Biography of the World's Most Famous Equation, Doubleday Canada, , 337 p.
- Le titre de l'ouvrage contient les mots « Famous Equation », qui se traduisent en français pas « fameuse équation ».
- (en) P Gibbs, « Why is c the symbol for the speed of light? », sur Usenet Physics FAQ, University of California, Riverside, (consulté le )
- « The origins of the letter c being used for the speed of light can be traced back to a paper of 1856 by Weber and Kohlrausch [...] Weber apparently meant c to stand for 'constant' in his force law, but there is evidence that physicists such as Lorentz and Einstein were accustomed to a common convention that c could be used as a variable for velocity. This usage can be traced back to the classic Latin texts in which c stood for 'celeritas', meaning 'speed'. »
- (en) K. S. Mendelson, « The story of c », American Journal of Physics, vol. 74, no 11, , p. 995-997 (DOI 10.1119/1.2238887, Bibcode 2006AmJPh..74..995M)
- Marc Séguin et Benoît Villeuneuve, Astronomie et astrophysique : Cinq grandes idées pour explorer et comprendre l'Univers, vol. 2, ERPI, , 618 p. (ISBN 978-2-7613-1184-7), p. 121
- Consulter par exemple :
- (en) D. R. Lide, CRC Handbook of Chemistry and Physics, CRC Press, (ISBN 978-0-8493-0485-9, lire en ligne), p. 2-9
- (en) J. W. Harris et al., Handbook of Physics, Springer, (ISBN 978-0-387-95269-7, lire en ligne), p. 499
- (en) J. C. Whitaker, The Electronics Handbook, CRC Press, (ISBN 978-0-8493-1889-4, lire en ligne), p. 235
- (en) E. R. Cohen, Quantities, Units and Symbols in Physical Chemistry, Royal Society of Chemistry, , 3e éd. (ISBN 978-0-85404-433-7, lire en ligne), p. 184
- (en) Bureau international des poids et mesures, The International System of Units (SI), 8th, (ISBN 92-822-2213-6, lire en ligne [PDF]), p. 112
- (en) G. Galilei, H. Crew et A. de Salvio (trad.), Dialogues Concerning Two New Sciences, Dover Publications, (1re éd. 1638) (ISBN 978-0-486-60099-4, lire en ligne), p. 43
- (en) C. B. Boyer, « Early Estimates of the Velocity of Light », Isis, vol. 33, no 1, , p. 24 (DOI 10.1086/358523, S2CID 145400212)
- (en) Renato Foschi et Matteo Leone, « Galileo, measurement of the velocity of light, and the reaction times », Perception, vol. 38, no 8, , p. 1252 (PMID 19817156, DOI 10.1068/p6263, hdl 2318/132957, S2CID 11747908)
- (en) Renato Foschi et Matteo Leone, « Galileo, measurement of the velocity of light, and the reaction times », Perception, vol. 38, no 8, , p. 1253 (PMID 19817156, DOI 10.1068/p6263, hdl 2318/132957, S2CID 11747908)
- (it) Lorenzo Magalotti, Saggi di Naturali Esperienze fatte nell' Accademia del Cimento, Florence, Istituto e Museo di Storia delle Scienze, (1re éd. 1667) (lire en ligne [numérique]), 265–66
- « Demonstration tovchant le mouvement de la lumiere trouvé par M. Rŏmer de l'Académie Royale des Sciences », Journal des sçavans, , p. 233-236 (lire en ligne [PDF])
- Traduit en anglais dans « A demonstration concerning the motion of light, communicated from Paris, in the Journal des Sçavans, and here made English », Philosophical Transactions of the Royal Society, vol. 12, no 136, , p. 893-895 (DOI 10.1098/rstl.1677.0024, Bibcode 1677RSPT...12..893.)
- Article reproduit dans (en) C. Hutton (dir.), G. Shaw (dir.) et R. Pearson (dir.), « On the Motion of Light by M. Romer », dans The Philosophical Transactions of the Royal Society of London, from Their Commencement in 1665, in the Year 1800: Abridged, vol. II. From 1673 to 1682, Londres, C. & R. Baldwin, (lire en ligne), p. 397-398
- Le rapport publié dans le Journal des sçavans est inspiré du rapport que Rømer a lu devant l'Académie des Sciences de la France en novembre 1676 (voir Cohen 1940, p. 346).
- Traduit en anglais dans « A demonstration concerning the motion of light, communicated from Paris, in the Journal des Sçavans, and here made English », Philosophical Transactions of the Royal Society, vol. 12, no 136, , p. 893-895 (DOI 10.1098/rstl.1677.0024, Bibcode 1677RSPT...12..893.)
- C. Huygens, Traitée de la Lumière, Pierre van der Aa, (lire en ligne), p. 8–9
- (en) P. Gibbs, « How is the speed of light measured? », sur Usenet Physics FAQ, University of California, Riverside, (consulté le )
- (en) L. Essen et A. C. Gordon-Smith, « The Velocity of Propagation of Electromagnetic Waves Derived from the Resonant Frequencies of a Cylindrical Cavity Resonator », Proceedings of the Royal Society of London A, vol. 194, no 1038, , p. 348-361 (DOI 10.1098/rspa.1948.0085, JSTOR 98293, Bibcode 1948RSPSA.194..348E)
- (en) E. B. Rosa et N. E. Dorsey, « A new determination of the ratio of the electromagnetic to the electrostatic unit of electricity », Bulletin of the Bureau of Standards, vol. 3, no 6, , p. 433 (DOI 10.6028/bulletin.070
 )
) - (en) A. A. Michelson, « Measurement of the Velocity of Light Between Mount Wilson and Mount San Antonio », The Astrophysical Journal, vol. 65, , p. 1 (DOI 10.1086/143021, Bibcode 1927ApJ....65....1M)
- (en) L. Essen, « The Velocity of Propagation of Electromagnetic Waves Derived from the Resonant Frequencies of a Cylindrical Cavity Resonator », Proceedings of the Royal Society of London A, vol. 204, no 1077, , p. 260-277 (DOI 10.1098/rspa.1950.0172, JSTOR 98433, Bibcode 1950RSPSA.204..260E, S2CID 121261770)
- (en) K. D. Froome, « A New Determination of the Free-Space Velocity of Electromagnetic Waves », Proceedings of the Royal Society of London. Series A, Mathematical and Physical Sciences, vol. 247, no 1248, , p. 109-122 (DOI 10.1098/rspa.1958.0172, JSTOR 100591, Bibcode 1958RSPSA.247..109F, S2CID 121444888)
- (en) K. M. Evenson et al., « Speed of Light from Direct Frequency and Wavelength Measurements of the Methane-Stabilized Laser », Physical Review Letters, vol. 29, no 19, , p. 1346-1349 (DOI 10.1103/PhysRevLett.29.1346, Bibcode 1972PhRvL..29.1346E, S2CID 120300510, lire en ligne)
- (en) « Resolution 1 of the 17th CGPM », BIPM, (consulté le )
- (en) John Weiner et Frederico Nunes, Light-Matter Interaction: Physics and Engineering at the Nanoscale, OUP Oxford, , édition illustrée (ISBN 978-0-19-856766-0, lire en ligne), p. 1
- (en) G. Sarton, Ancient science through the golden age of Greece, Courier Dover, (ISBN 978-0-486-27495-9, lire en ligne), p. 248
- (en) R. H. MacKay et R. W. Oldford, « Scientific Method, Statistical Method and the Speed of Light », Statistical Science, vol. 15, no 3, , p. 254–78 (DOI 10.1214/ss/1009212817, lire en ligne) (cliquer sur Historical background dans la table des matières)
- (en) Sherif Sayed Ahmed, Electronic Microwave Imaging with Planar Multistatic Arrays, Logos Verlag Berlin, (ISBN 978-3-8325-3621-3, lire en ligne), p. 1
- (en) C. G. Gross, « The Fire That Comes from the Eye », Neuroscientist, vol. 5, , p. 58–64 (DOI 10.1177/107385849900500108, S2CID 84148912)
- (en) S. Hamarneh, « Review: Hakim Mohammed Said, Ibn al-Haitham », Isis, vol. 63, no 1, , p. 119 (DOI 10.1086/350861)
- (en) P. M. Lester, Visual Communication: Images With Messages, Thomson Wadsworth, , 10–11 p. (ISBN 978-0-534-63720-0)
- (en) J. J. O'Connor et E. F. Robertson, « Abu Ali al-Hasan ibn al-Haytham », sur MacTutor History of Mathematics archive, University of St Andrews (consulté le )
- (en) P. Lauginie (2004) « Measuring Speed of Light: Why? Speed of what? » dans Fifth International Conference for History of Science in Science Education : 75–84 p.. Consulté le 12 août 2017.
- (en) J. J. O'Connor et E. F. Robertson, « Abu han Muhammad ibn Ahmad al-Biruni », sur MacTutor History of Mathematics archive, University of St Andrews (consulté le )
- (en) D. C. Lindberg, Roger Bacon and the origins of Perspectiva in the Middle Ages: a critical edition and English translation of Bacon's Perspectiva, with introduction and notes, Oxford University Press, (ISBN 978-0-19-823992-5, lire en ligne), p. 143
- (en) D. C. Lindberg, « Late Thirteenth-Century Synthesis in Optics », dans Edward Grant, A source book in medieval science, Harvard University Press, (ISBN 978-0-674-82360-0, lire en ligne), p. 396
- (en) P. Marshall, « Nicole Oresme on the Nature, Reflection, and Speed of Light », Isis, vol. 72, no 3, , p. 357–374 [367–374] (DOI 10.1086/352787, S2CID 144035661)
- (en) Florian Cajori, A History of Physics in its Elementary Branches: Including the Evolution of Physical Laboratories,
- (en) Carl Benjamin Boyer, The Rainbow: From Myth to Mathematics,
- (en) I. B. Cohen, « Roemer and the first determination of the velocity of light (1676) », Isis, vol. 31, no 2, , p. 327–79 (DOI 10.1086/347594, hdl 2027/uc1.b4375710, S2CID 145428377, lire en ligne)
- (la) I. Newton, Optiks, (lire en ligne), « Prop. XI »
- Le texte de la Prop. XI est identique dans les éditions de 1704 et de 1719.
- (en) J. Bradley, « Account of a new discovered Motion of the Fix'd Stars », Philosophical Transactions, vol. 35, , p. 637-660 (lire en ligne)
- (en) M. Guarnieri, « Two Millennia of Light: The Long Path to Maxwell's Waves », IEEE Industrial Electronics Magazine, vol. 9, no 2, , p. 54–56, 60 (DOI 10.1109/MIE.2015.2421754, S2CID 20759821)
- (de) G. Kirchhoff, « Über die Bewegung der Elektricität », Ann. Phys., vol. 178, no 12, , p. 529–44 (DOI 10.1002/andp.18571781203, Bibcode 1857AnP...178..529K, lire en ligne)
- (en) Nicholas J. Giordano, College physics: reasoning and relationships, Cengage Learning, (ISBN 978-0-534-42471-8, lire en ligne), p. 787 Extract of page 787
- (en) Peter Gabriel Bergmann, The riddle of gravitation, Courier Dover Publications, (ISBN 978-0-486-27378-5, lire en ligne), p. 17 Extract of page 17
- (en) Sander Bais, The Equations: Icons of knowledge, Harvard University Press, (ISBN 978-0-674-01967-6, lire en ligne), p. 40
- (en) J. J. O'Connor et E. F. Robertson, « James Clerk Maxwell », School of Mathematics and Statistics, University of St Andrews,
- Richard Feynman (trad. Françoise Balibar et Alain Laverne), Lumière et Matière : Une étrange histoire [« QED, The Strange Theory of Light and Matter »], InterÉditions, coll. « Sciences », (1re éd. 1987), 206 p. (ISBN 2-7296-0154-6), p. 17.
- Serway 1992, p. 320.
- Serway 1992, p. 323.
- Serway 1992, p. 321.
- (en) Maurizio Consoli et Alessandro Pluchino, Michelson-Morley Experiments: An Enigma for Physics & The History of Science, World Scientific, (ISBN 978-9-813-27818-9, lire en ligne), p. 118-119
- (en) A. A. Michelson et E. W. Morley, « On the Relative Motion of the Earth and the Luminiferous Ether », American Journal of Science, vol. 34, no 203, , p. 333–345 (DOI 10.1366/0003702874447824, S2CID 98374065, lire en ligne)
- (en) A. P. French, Special relativity, Van Nostrand Reinhold, (ISBN 978-0-442-30782-0), p. 51–57
- (en) O. Darrigol, Electrodynamics from Ampère to Einstein, Clarendon Press, (ISBN 978-0-19-850594-5, lire en ligne)
- (en) P. Galison, Einstein's Clocks, Poincaré's Maps: Empires of Time, W.W. Norton, (ISBN 978-0-393-32604-8)
- Serway 1992, p. 323-324.
- (en) A. I. Miller, Albert Einstein's special theory of relativity. Emergence (1905) and early interpretation (1905–1911), Addison–Wesley, (ISBN 978-0-201-04679-3, lire en ligne)
- (en) A. Pais, Subtle is the Lord: The Science and the Life of Albert Einstein, Oxford University Press, (ISBN 978-0-19-520438-4)
- (en) « Resolution 1 of the 15th CGPM », BIPM, (consulté le )
- (en) « Resolution 6 of the 15th CGPM », BIPM, (consulté le )
- (en) R. Barger et J. Hall, « Wavelength of the 3.39-μm laser-saturated absorption line of methane », Applied Physics Letters, vol. 22, no 4, , p. 196 (DOI 10.1063/1.1654608, Bibcode 1973ApPhL..22..196B, S2CID 1841238, lire en ligne)
- (en) « Resolution 2 of the 15th CGPM », BIPM, (consulté le )
- (en) E. F. Taylor et J. A. Wheeler, Spacetime Physics: Introduction to Special Relativity, Macmillan, , 2e éd. (ISBN 978-0-7167-2327-1, lire en ligne)
- (en) W. B. Penzes, « Time Line for the Definition of the Meter » [PDF], NIST, (consulté le )
- (en) R. Penrose, The Road to Reality: A Complete Guide to the Laws of the Universe, Vintage Books, (ISBN 978-0-679-77631-4, lire en ligne), p. 410-411
- « [...] the most accurate standard for the metre is conveniently defined so that there are exactly 299 792 458 of them to the distance travelled by light in a standard second, giving a value for the metre that very accurately matches the now inadequately precise standard metre rule in Paris. »
- (en) J. Jespersen, J. Fitz-Randolph et J. Robb, From Sundials to Atomic Clocks: Understanding Time and Frequency, Courier Dover, , Reprint of National Bureau of Standards 1977, 2nd éd. (ISBN 978-0-486-40913-9, lire en ligne), p. 280
- (en) S. Adams, Relativity: An Introduction to Space–Time Physics, CRC Press, (ISBN 978-0-7484-0621-0, lire en ligne), p. 140
- « One peculiar consequence of this system of definitions is that any future refinement in our ability to measure c will not change the speed of light (which is a defined number), but will change the length of the meter! »
- (en) W. Rindler, Relativity: Special, General, and Cosmological, Oxford University Press, , 2e éd. (ISBN 978-0-19-856731-8, lire en ligne), p. 41
- « Note that [...] improvements in experimental accuracy will modify the meter relative to atomic wavelengths, but not the value of the speed of light! »
- (en) « The "explicit-constant" formulation », sur BIPM,
- (en) « Base unit definitions: Second », sur physics.nist.gov (consulté le )
- Conférence générale des poids et mesures - Comptes rendus de la 26e réunion de la CGPM, Bureau international des poids et mesures, (lire en ligne [PDF]), « Annexe 3. Les unités de base du SI », p. 212
- (en) B. Sriranjan, « Postulates of the special theory of relativity and their consequences », dans The Special Theory to Relativity, PHI Learning Pvt. Ltd., (ISBN 978-81-203-1963-9, lire en ligne), p. 20 et suiv.
- (en) R. d'Inverno, Introducing Einstein's Relativity, Oxford University Press, (ISBN 978-0-19-859686-8, lire en ligne), p. 19-20
- (en) J. J. Stachel, Einstein from "B" to "Z" – Volume 9 of Einstein studies, Springer, (ISBN 978-0-8176-4143-6, lire en ligne), p. 226
- (de) A. Einstein, « Zur Elektrodynamik bewegter Körper », Annalen der Physik, vol. 17, no 10, , p. 890-921 (DOI 10.1002/andp.19053221004
 , Bibcode 1905AnP...322..891E, lire en ligne)
, Bibcode 1905AnP...322..891E, lire en ligne)
- Traduit en anglais : (en) W. Perrett (trad. G. B. Jeffery), « On the Electrodynamics of Moving Bodies », sur Fourmilab, J. Walker
- Traduit en français à partir d'une version publiée par le physicien indien Meghnad Saha en 1920 : Albert Einstein (trad. Cantons-de-l'Est et Simon Villeneuve), « De l'électrodynamique des corps en mouvement », sur Les Classiques des sciences sociales,
- Serway 1992, p. 324.
- (en) J.-P. Hsu et Y. Z. Zhang, Lorentz and Poincaré Invariance, vol. 8, World Scientific, coll. « Advanced Series on Theoretical Physical Science », (ISBN 978-981-02-4721-8, lire en ligne), p. 543 et suiv.
- (en) Y. Z. Zhang, Special Relativity and Its Experimental Foundations, vol. 4, World Scientific, coll. « Advanced Series on Theoretical Physical Science », (ISBN 978-981-02-2749-4, lire en ligne), p. 172–173
- (en) T. Roberts (dir.) et S. Schleif, « What is the experimental basis of Special Relativity? », sur Usenet Physics FAQ, University of California, Riverside,
- (en) J.-P. Uzan et B. Leclercq, The Natural Laws of the Universe: Understanding Fundamental Constants, Springer, (ISBN 978-0-387-73454-5, lire en ligne), p. 43–44
- James H. Smith, Introduction à la relativité, InterEditions, , chap. 4 (« §4 Le paradoxe des longueurs et la simultanéité »)
- Réédité par Masson (Dunod, 3e édition, 1997).
- (en) J. Terrell, « Invisibility of the Lorentz Contraction », Physical Review, vol. 116, no 4, , p. 1041-1045 (DOI 10.1103/PhysRev.116.1041, Bibcode 1959PhRv..116.1041T)
- (en) R. Penrose, « The Apparent Shape of a Relativistically Moving Sphere », Proceedings of the Cambridge Philosophical Society, vol. 55, no 1, , p. 137–39 (DOI 10.1017/S0305004100033776, Bibcode 1959PCPS...55..137P)
- David Langlois, Introduction à la relativité : Principes fondamentaux et conséquences physiques, Vuibert, , 192 p., p. 16-19
- Taillet, Villain et Febvre 2013, s.v.facteur de Lorentz, p. 269, col. 2.
- Douglas C. Giancoli, Paul-Étienne Ouellet (adaptation), Louis-André Hamel (consult. scient.) et J. M. Luc Ouellet (consult. scient.), Physique générale : Ondes, optique et physique moderne, vol. 3 : Ondes, optique et physique moderne, de boeck, , 488 p. (ISBN 2-8041-1702-2, lire en ligne), p. 207
- (en) Graham Woan, The Cambridge Handbook of Physics, Cambridge University Press, (ISBN 0521575079), p. 64 (consulter le graphique)
- (en) J. B. Hartle, Gravity: An Introduction to Einstein's General Relativity, Addison-Wesley, (ISBN 978-981-02-2749-4, lire en ligne), p. 52-59
- (en) J. B. Hartle, Gravity: An Introduction to Einstein's General Relativity, Addison-Wesley, (ISBN 978-981-02-2749-4), p. 332
- (en) G. Schäfer et M. H. Brügmann, « Propagation of light in the gravitational field of binary systems to quadratic order in Newton's gravitational constant: Part 3: 'On the speed-of-gravity controversy' », dans H. Dittus, C. Lämmerzahl et S. G. Turyshev, Lasers, clocks and drag-free control: Exploration of relativistic gravity in space, Springer, (ISBN 978-3-540-34376-9, lire en ligne)
- (en) P. Gibbs (dir.) et S. Carlip, « Is The Speed of Light Constant? », sur Usenet Physics FAQ, University of California, Riverside, (consulté le )
- (en) G. F. R. Ellis et J.-P. Uzan, « 'c' is the speed of light, isn't it? », American Journal of Physics, vol. 73, no 3, , p. 240-327 (DOI 10.1119/1.1819929, Bibcode 2005AmJPh..73..240E, arXiv gr-qc/0305099, S2CID 119530637)
- « The possibility that the fundamental constants may vary during the evolution of the universe offers an exceptional window onto higher dimensional theories and is probably linked with the nature of the dark energy that makes the universe accelerate today. »
- (en) D. F. Mota, Variations of the Fine Structure Constant in Space and Time, (Bibcode 2004astro.ph..1631M, arXiv astro-ph/0401631) (thèse doctorale)
- (en) J.-P. Uzan, « The fundamental constants and their variation: observational status and theoretical motivations », Reviews of Modern Physics, vol. 75, no 2, , p. 403 (DOI 10.1103/RevModPhys.75.403, Bibcode 2003RvMP...75..403U, arXiv hep-ph/0205340, S2CID 118684485)
- (en) G. Amelino-Camelia, « Quantum Gravity Phenomenology », Living Reviews in Relativity, vol. 16, no 1, , p. 5 (PMID 28179844, PMCID 5255913, DOI 10.12942/lrr-2013-5, Bibcode 2013LRR....16....5A, arXiv 0806.0339)
- (en) R. L. Walsworth, « Tests of Lorentz Symmetry in the Spin-Coupling Sector », dans Jürgen Ehlers et Claus Lämmerzahl, Special Relativity, vol. 702, Springer, (ISBN 978-3-540-34522-0, DOI 10.1007/3-540-34523-X_18), p. 493-505
- (en) S. Herrmann, A. Senger, K. Möhle, M. Nagel, E. V. Kovalchuk et A. Peters, « Rotating optical cavity experiment testing Lorentz invariance at the 10−17 level », Physical Review D, vol. 80, no 100, , p. 105011 (DOI 10.1103/PhysRevD.80.105011, Bibcode 2009PhRvD..80j5011H, arXiv 1002.1284, S2CID 118346408)
- (en) K. R. Lang, Astrophysical formulae, Birkhäuser, , 3e éd. (ISBN 978-3-540-29692-8, lire en ligne), p. 152
- (en) Deborah Netburn, « It's official: Time machines won't work », sur Los Angeles Times,
- (en) « HKUST Professors Prove Single Photons Do Not Exceed the Speed of Light », sur The Hong Kong University of Science and Technology,
- (en) Shanchao Zhang, J.F. Chen, Chang Liu, M.M.T. Loy, G.K.L. Wong et Shengwang Du, « Optical Precursor of a Single Photon », Phys. Rev. Lett., vol. 106, no 243602, , p. 243602 (PMID 21770570, DOI 10.1103/physrevlett.106.243602, Bibcode 2011PhRvL.106x3602Z, lire en ligne [PDF])
- (en) M. Fowler, Notes on Special Relativity, University of Virginia, (lire en ligne [PDF]), p. 56
- (en) S. Liberati, S. Sonego et M. Visser, « Faster-than-c signals, special relativity, and causality », Annals of Physics, vol. 298, no 1, , p. 167-185 (DOI 10.1006/aphy.2002.6233, Bibcode 2002AnPhy.298..167L, arXiv gr-qc/0107091, S2CID 48166)
- (en) E. F. Taylor et J. A. Wheeler, Spacetime Physics, W. H. Freeman, (ISBN 978-0-7167-2327-1, lire en ligne), p. 74-75
- (en) R. C. Tolman, The Theory of the Relativity of Motion, BiblioLife, (1re éd. 1917) (ISBN 978-1-103-17233-7), « Velocities greater than that of light », p. 54
- (de) Albert Einstein, « Über das Relativitätsprinzip und die aus demselben gezogenen Folgerungen » [« On the relativity principle and the conclusions drawn from it »], Jahrbuch der Radioaktivität und Elektronik, vol. 4, , p. 411-462 (lire en ligne [PDF])
- (en) Albert Einstein, « On the relativity principle and the conclusions drawn from it », dans John Stachel, David C. Cassidy, Jürgen Renn et Robert Schulmann, The Collected Papers of Albert Einstein, Volume 2: The Swiss Years: Writings, 1900-1909, Princeton, Princeton University Press, (ISBN 9780691085265, lire en ligne), p. 252
- (en) A. I. Miller, Albert Einstein's special theory of relativity. Emergence (1905) and early interpretation (1905–1911), Reading, Addison–Wesley, (ISBN 0-201-04679-2, lire en ligne)
- (en) R. C. Tolman, « Velocities greater than that of light », dans The theory of the Relativity of Motion, University of California Press, (OCLC 13129939, lire en ligne), p. 54
- (en) Gregory Benford, D. L. Book et W. A. Newcomb, « The Tachyonic Antitelephone », Physical Review D, vol. 2, no 2, , p. 263-265 (DOI 10.1103/PhysRevD.2.263, Bibcode 1970PhRvD...2..263B, S2CID 121124132, lire en ligne [PDF])
- (en) I. D. Lawrie, « Appendix C: Natural units », dans A Unified Grand Tour of Theoretical Physics, CRC Press, , 2e éd. (ISBN 978-0-7503-0604-1, lire en ligne), p. 540
- (en) L. Hsu, « Appendix A: Systems of units and the development of relativity theories », dans A Broader View of Relativity: General Implications of Lorentz and Poincaré Invariance, World Scientific, , 2e éd. (ISBN 978-981-256-651-5, lire en ligne), p. 427-428
- (en) E. Hecht, Optics, Addison-Wesley, , 2e éd. (ISBN 978-0-201-11609-0), p. 62
- (en) R. S. Quimby, Photonics and lasers: An introduction, John Wiley and Sons, (ISBN 978-0-471-71974-8, lire en ligne), p. 9
- (en) M. Wertheim, « The Shadow Goes », The New York Times, (lire en ligne, consulté le )
- (en) P. Gibbs, « Is Faster-Than-Light Travel or Communication Possible? », sur Usenet Physics FAQ, University of California, Riverside,
- (en) S. F. Tuan (dir.) et J. J. Sakurai, Modern Quantum Mechanics, Addison-Wesley, (ISBN 978-0-201-53929-5, lire en ligne), p. 231-232
- (en) J. G. Muga (dir.), R. S. Mayato (dir.) et I. L. Egusquiza (dir.), Time in Quantum Mechanics, Springer, (ISBN 978-3-540-73472-7, lire en ligne), p. 48
- (en) H. E. Hernández-Figueroa, M. Zamboni-Rached et E. Recami, Localized Waves, Wiley Interscience, (ISBN 978-0-470-10885-7, lire en ligne), p. 26
- (en) K. Wynne, « Causality and the nature of information », Optics Communications, vol. 209, nos 1-3, , p. 84-100 (DOI 10.1016/S0030-4018(02)01638-3, Bibcode 2002OptCo.209...85W, lire en ligne [PDF])
- (en) M. Rees, « The Appearance of Relativistically Expanding Radio Sources », Nature, vol. 211, no 5048, , p. 468 (DOI 10.1038/211468a0, Bibcode 1966Natur.211..468R, S2CID 41065207)
- (en) I. P. Chase, « Apparent Superluminal Velocity of Galaxies », sur Usenet Physics FAQ, University of California, Riverside (consulté le )
- Tegmark 2018, p. 74.
- Tegmark 2018, p. 75-76.
- (en) E. R. Harrison, Masks of the Universe, Cambridge University Press, (ISBN 978-0-521-77351-5, lire en ligne), p. 206
- (en) W. K. H. Panofsky et M. Phillips, Classical Electricity and Magnetism, Addison-Wesley, (ISBN 978-0-201-05702-7, lire en ligne), p. 182
- Feynman 1992, p. 109.
- Hladik 2008, p. 185.
- (en) B. E. Schaefer, « Severe limits on variations of the speed of light with frequency », Physical Review Letters, vol. 82, no 25, , p. 4964–66 (DOI 10.1103/PhysRevLett.82.4964, Bibcode 1999PhRvL..82.4964S, arXiv astro-ph/9810479, S2CID 119339066)
- (en) J. Ellis, N. E. Mavromatos, D. V. Nanopoulos et A. S. Sakharov, « Quantum-Gravity Analysis of Gamma-Ray Bursts using Wavelets », Astronomy & Astrophysics, vol. 402, no 2, , p. 409-424 (DOI 10.1051/0004-6361:20030263, Bibcode 2003A&A...402..409E, arXiv astro-ph/0210124, S2CID 15388873)
- (en) M. Füllekrug, « Probing the Speed of Light with Radio Waves at Extremely Low Frequencies », Physical Review Letters, vol. 93, no 4, , p. 043901 (PMID 15323762, DOI 10.1103/PhysRevLett.93.043901, Bibcode 2004PhRvL..93d3901F)
- (en) E. Adelberger, G. Dvali et A. Gruzinov, « Photon Mass Bound Destroyed by Vortices », Physical Review Letters, vol. 98, no 1, , p. 010402 (PMID 17358459, DOI 10.1103/PhysRevLett.98.010402, Bibcode 2007PhRvL..98a0402A, arXiv hep-ph/0306245, S2CID 31249827)
- (en) B. G. Sidharth, The Thermodynamic Universe, World Scientific, (ISBN 978-981-281-234-6, lire en ligne), p. 134
- (en) G. Amelino-Camelia, « Astrophysics: Burst of support for relativity », Nature, vol. 462, no 7271, , p. 291–92 (PMID 19924200, DOI 10.1038/462291a, Bibcode 2009Natur.462..291A, S2CID 205051022)
- (en) Sylvan C. Bloch, « Eight velocities of light », American Journal of Physics, vol. 45, no 6, , p. 538-549 (DOI 10.1119/1.10953, lire en ligne [PDF], consulté le )
- (en) Richard L. Smith, « The velocities of light », American Journal of Physics, vol. 38, no 8, , p. 978-984 (DOI 10.1119/1.1976551, Bibcode 1970AmJPh..38..978S)
- (en) M. de Podesta, Understanding the Properties of Matter, CRC Press, (ISBN 978-0-415-25788-6, lire en ligne), p. 131
- (en) « Optical constants of H2O, D2O (Water, heavy water, ice) », sur refractiveindex.info, Mikhail Polyanskiy (consulté le )
- (en) « Optical constants of Soda lime glass », sur refractiveindex.info, Mikhail Polyanskiy (consulté le )
- (en) « Optical constants of C (Carbon, diamond, graphite) », sur refractiveindex.info, Mikhail Polyanskiy (consulté le )
- (en) William J. Cromie, « Researchers now able to stop, restart light », sur Harvard University Gazette,
- (en) P. W. Milonni, Fast light, slow light and gauche-handed light, CRC Press, (ISBN 978-0-7503-0926-4, lire en ligne), p. 25
- (en) J. S. Toll, « Causality and the Dispersion Relation: Logical Foundations », Physical Review, vol. 104, no 6, , p. 1760–70 (DOI 10.1103/PhysRev.104.1760, Bibcode 1956PhRv..104.1760T)
- (en) L. V. Hau, S. E. Harris, Z. Dutton et C. H. Behroozi, « Light speed reduction to 17 metres per second in an ultracold atomic gas », Nature, vol. 397, no 6720, , p. 594-598 (DOI 10.1038/17561, Bibcode 1999Natur.397..594V, S2CID 4423307, lire en ligne [PDF])
- (en) C. Liu, Z. Dutton, C. H. Behroozi et L. V. Hau, « Observation of coherent optical information storage in an atomic medium using halted light pulses », Nature, vol. 409, no 6819, , p. 490–93 (PMID 11206540, DOI 10.1038/35054017, Bibcode 2001Natur.409..490L, S2CID 1894748, lire en ligne [PDF])
- (en) M. Bajcsy, A. S. Zibrov et M. D. Lukin, « Stationary pulses of light in an atomic medium », Nature, vol. 426, no 6967, , p. 638-641 (PMID 14668857, DOI 10.1038/nature02176, Bibcode 2003Natur.426..638B, arXiv quant-ph/0311092, S2CID 4320280)
- (en) B. Dumé, « Switching light on and off », sur Physics World, Institute of Physics,
- (en) D. Whitehouse, « Beam Smashes Light Barrier », BBC News, (lire en ligne, consulté le )
- (en) P. W. Milonni, Fast light, slow light and gauche-handed light, CRC Press, (ISBN 978-0-7503-0926-4, lire en ligne), chap. 2 (« The Refractive index can be negative »)
- (ru) Pavel A. Cherenkov, « Видимое свечение чистых жидкостей под действием γ-радиации » [« Visible emission of pure liquids by action of γ radiation »], Doklady Akademii Nauk SSSR, vol. 2, , p. 451
- Réimprimé : (ru) P. A. Cherenkov, « Видимое свечение чистых жидкостей под действием γ-радиации » [« Visible emission of pure liquids by action of γ radiation »], Usp. Fiz. Nauk, vol. 93, no 10, , p. 385 (DOI 10.3367/ufnr.0093.196710n.0385)
- Réimprimé : (ru) A. N. Gorbunov et E. P. Čerenkova, Pavel Alekseyevich Čerenkov: Chelovek i Otkrytie [« Pavel Alekseyevich Čerenkov: Man and Discovery »], Moscou, Nauka, , p. 149-153
- « Strock - Verre - Tensions », sur strock.pi.r2.3.14159.free.fr (consulté le )
- (en) B. Parhami, Introduction to parallel processing: algorithms and architectures, Plenum Press, (ISBN 978-0-306-45970-2, lire en ligne), p. 5
- (en) (2009) « Software Transactional Memories: An Approach for Multicore Programming » dans 10th International Conference, PaCT 2009, Novosibirsk, Russia, 31 August – 4 September 2009 , Springer, p. 26.
- (en) Wesley W. Stout, Radar: The Great Detective, Chrysler Corporation, , p. 4, 6 et 10 (consulter les pages en ligne: 4, 6 et 10)
- (en) « Modern Navigation », sur math.nus.edu.sg,
- (en) J.O. Dickey et al., « Lunar Laser Ranging: A Continuing Legacy of the Apollo Program », Science, vol. 265, no 5171, , p. 482–90 (PMID 17781305, DOI 10.1126/science.265.5171.482, Bibcode 1994Sci...265..482D, S2CID 10157934, lire en ligne [PDF])
- (en) E. M. Standish, « The JPL planetary ephemerides », Celestial Mechanics, vol. 26, no 2, , p. 181-186 (DOI 10.1007/BF01230883, Bibcode 1982CeMec..26..181S)
- (en) J. B. Berner, S. H. Bryant et P. W. Kinman, « Range Measurement as Practiced in the Deep Space Network », Proceedings of the IEEE, vol. 95, no 11, , p. 2202–2214 (DOI 10.1109/JPROC.2007.905128, S2CID 12149700, lire en ligne [PDF])
- (en) J. E. Midwinter, Optical Fibers for Transmission, Krieger Publishing Company, , 2nd éd. (ISBN 978-0-89464-595-2)
- (en) « Theoretical vs real-world speed limit of Ping », sur Pingdom, (consulté le )
- « Combien de temps faut-il à la lumière réfléchie par la Lune pour parvenir jusqu'à nous ? », sur etoile-des-enfants.ch, L'Étoile des enfants (consulté le )
- (en) « Day 4: Lunar Orbits 7, 8 and 9 », sur The Apollo 8 Flight Journal, NASA (consulté le )
- (en) « Communications », sur Mars 2020 Mission Perseverence Rover, NASA (consulté le )
- (en) Ray Villard, « Hubble Reaches the "Undiscovered Country" of Primeval Galaxies », sur nasa.gov, Space Telescope Science Institute,
- (en) The Hubble Ultra Deep Field Lithograph, NASA, (lire en ligne [PDF]), p. 1
- (en) « The IAU and astronomical units », International Astronomical Union (consulté le )
- (en) « 9461 billion km », WolframAlpha, (consulter la section Unit conversions)
- Laurent Sacco, « Détectera-t-on bientôt une exoterre autour d'Alpha du Centaure ? », Futura-Sciences, (lire en ligne)
- (en) « Time is money when it comes to microwaves », Financial Times, (lire en ligne, consulté le )
- (en) Mark Buchanan, « Physics in finance: Trading at the speed of light », Nature, vol. 518, no 7538, , p. 161-163 (PMID 25673397, DOI 10.1038/518161a
 , Bibcode 2015Natur.518..161B)
, Bibcode 2015Natur.518..161B) - (en) P. H. Sydenham, « Measurement of length », dans W. Boyes, Instrumentation Reference Book, Butterworth–Heinemann, , 3e éd. (ISBN 978-0-7506-7123-1, lire en ligne), p. 56
- « [...] if the speed of light is defined as a fixed number then, in principle, the time standard will serve as the length standard[...] »
- (en) « CODATA value: Speed of Light in Vacuum », sur The NIST reference on Constants, Units, and Uncertainty, NIST (consulté le )
- Cours d'optique, École normale supérieure, (lire en ligne [PDF]), p. 3
- (la) Ole Rømer, « Correspondance 1676-1684 », dans J. Bosscha, Œuvres complètes de Christiaan Huygens (1888-1950), vol. VIII, La Haye, Martinus Nijhoff, , p. 32-35
- Francis Beaubois, « Rœmer et la vitesse de la lumière », sur bibnum.education.fr, (consulter l'onglet « Analyse »).
- Dans son rapport à l'Académie des sciences, Rømer écrit :
- « Cette seconde inégalité semble être due au fait que la lumière met un certain temps à nous parvenir depuis le satellite ; la lumière semble prendre environ dix à onze minutes [pour franchir] une distance égale au demi-diamètre de l'orbite terrestre. »
- (en) Laurence Bobis et James Lequeux, « Cassini, Rømer and the Velocity of Light », J. Astron. Hist. Héritage, vol. 11, no 2, , p. 97-105 (Bibcode 2008JAHH...11...97B, lire en ligne [PDF])
- « Cette seconde inégalité semble être due au fait que la lumière met un certain temps à nous parvenir depuis le satellite ; la lumière semble prendre environ dix à onze minutes [pour franchir] une distance égale au demi-diamètre de l'orbite terrestre. »
- (en) A. Wróblewski, « De Mora Luminis: a spectacle in two acts with a prologue and an epilogue », American Journal of Physics, vol. 53, , p. 620-630
- (en) P. Duffett-Smith, Practical Astronomy with your Calculator, Cambridge University Press, (ISBN 978-0-521-35699-2, lire en ligne
 ), p. 62
), p. 62 - (en) « Resolution B2 on the re-definition of the astronomical unit of length » [PDF], International Astronomical Union,
- (en) « Supplement 2014: Updates to the 8th edition (2006) of the SI Brochure », International Bureau of Weights and Measures, , p. 14 (lire en ligne [PDF])
- (en) Bureau international des poids et mesures, The International System of Units (SI), 8th, (ISBN 92-822-2213-6, lire en ligne [PDF]), p. 126
- (en) E. V. Pitjeva et E. M. Standish, « Proposals for the masses of the three largest asteroids, the Moon–Earth mass ratio and the Astronomical Unit », Celestial Mechanics and Dynamical Astronomy, vol. 103, no 4, , p. 365-372 (DOI 10.1007/s10569-009-9203-8, Bibcode 2009CeMDA.103..365P, S2CID 121374703, lire en ligne)
- (en) IAU Working Group on Numerical Standards for Fundamental Astronomy, « IAU WG on NSFA Current Best Estimates », US Naval Observatory
- (en) « Astrodynamic Constants », sur Solar System Dynamics, Jet Propulsion Laboratory (consulté le )
- (en) « NPL's Beginner's Guide to Length », UK National Physical Laboratory (consulté le )
- (en) H. H. Dunn, « Test Light Speed in Mile-Long Vacuum Tube », Popular Science, New York, vol. 117, no 3, , p. 17-18, 132 et 133 (lire en ligne)
- Le Patrimoine des communes des Hauts-de-Seine, Flohic éditions, , p. 383.
- Matthieu Frachon, avec le concours de la Société d'histoire de Suresnes, « Que la lumière soit... », Suresnes Mag, no 311, , p. 40-41 (lire en ligne).
- Jean-Jacques Samueli, « L’expérience du miroir tournant de Foucault », sur bibnum.education.fr, (consulter l'onglet « Actualité »)
- (en) M. Fowler, « The Speed of Light », University of Virginia (consulté le )
- (en) J. Cooke, M. Martin, H. McCartney et B. Wilf, « Direct determination of the speed of light as a general physics laboratory experiment », American Journal of Physics, vol. 36, no 9, , p. 847 (DOI 10.1119/1.1975166, Bibcode 1968AmJPh..36..847C)
- (en) K. Aoki et T. Mitsui, « A small tabletop experiment for a direct measurement of the speed of light », American Journal of Physics, vol. 76, no 9, , p. 812-815 (DOI 10.1119/1.2919743, Bibcode 2008AmJPh..76..812A, arXiv 0705.3996, S2CID 117454437)
- (en) M. B. James, R. B. Ormond et A. J. Stasch, « Speed of light measurement for the myriad », American Journal of Physics, vol. 67, no 8, , p. 681-714 (DOI 10.1119/1.19352, Bibcode 1999AmJPh..67..681J)
- « L’expérience OPERA annonce une anomalie dans le temps de vol des neutrinos allant du CERN au Gran Sasso », CERN, (communiqué de presse).
- (en) T. Adam et al., « Measurement of the neutrino velocity with the OPERA detector in the CNGS beam », Journal of High Energy Physics, vol. 2012, no 93, (DOI 10.1007/JHEP10(2012)093, arXiv 1109.4897)
- Sylvestre Huet, « Neutrinos plus rapides que la lumière ? Non et fin de l'histoire », sur sciences.blogs.liberation.fr, (consulté le ).
- Serway 1992, p. 111.
- (en) Philip Gibbs, « How is the speed of light measured? », The Physics and Relativity FAQ,
- Serway 1992, p. 133.
- (en) L. Essen, « Velocity of Electromagnetic Waves », Nature, vol. 159, no 4044, , p. 611-612 (DOI 10.1038/159611a0, Bibcode 1947Natur.159..611E, S2CID 4101717)
- (en) R. H. Stauffer, « Finding the Speed of Light with Marshmallows », The Physics Teacher, vol. 35, no 4, , p. 231 (DOI 10.1119/1.2344657, Bibcode 1997PhTea..35..231S, lire en ligne, consulté le )
- (en) « BBC Look East at the speed of light », sur BBC Norfolk website (consulté le )
- Une présentation détaillée de l'interféromètre et de son usage pour calculer c se trouve dans :
- (en) J. M. Vaughan, The Fabry-Perot interferometer, CRC Press, (ISBN 978-0-85274-138-2), p. 47 et 384-391
- (en) D. B. Sullivan, « Speed of Light from Direct Frequency and Wavelength Measurements », dans D. R. Lide, A Century of Excellence in Measurements, Standards, and Technology, CRC Press, (ISBN 978-0-8493-1247-2, lire en ligne [PDF]), p. 191-193
Annexes
Bibliographie
- François Arago, « Mémoire sur la vitesse de la lumière, lu à la première Classe de l'Institut, le 10 décembre 1810 », Comptes rendus hebdomadaires des séances de l'Académie des sciences, vol. 36, , p. 38-49 (lire en ligne)
- Jean Eisenstaedt et Michel Combes, « Arago et la vitesse de la lumière (1806-1810), un manuscrit inédit, une nouvelle analyse », Revue d'histoire des sciences, vol. 64, , p. 59-120 (lire en ligne)
- Richard Feynman (trad. Françoise Balibar et Alain Laverne), Lumière et Matière : Une étrange histoire [« QED, The Strange Theory of Light and Matter »], InterÉditions, coll. « Sciences », (1re éd. 1987), 206 p. (ISBN 978-2-02-014758-3).
 .
. - Jean Hladik, Pour comprendre simplement les origines et l'évolution de la Physique quantique, Paris, Ellipses, , 320 p. (ISBN 978-2-7298-3738-9).
 .
. - (en) Brian Luzum, Nicole Capitaine, Agnès Fienga, William Folkner, Toshio Fukushima, James Hilton, Catherine Hohenkerk, George Krasinsky, Gérard Petit, Elena Pitjeva, Michael Soffel et Patrick Wallace, « The IAU 2009 system of astronomical constants: the report of the IAU working group on numerical standards for Fundamental Astronomy », Celest Mech Dyn Astr, vol. 110, no 4, , p. 296 (DOI 10.1007/s10569-011-9352-4, Bibcode 2011CeMDA.110..293L, S2CID 122755461, lire en ligne [PDF]).

- Raymond A. Serway (trad. Robert Morin et Céline Temblay), Physique III : Optique et physique moderne [« Physics for Scientists and Engineers / With Modern Physics. Volume 3 »], Laval (Québec), Éditions Études Vivantes, , 3e éd., 776 p. (ISBN 2-7607-0542-0).

- Max Tegmark (trad. Benoît Clenet), Notre univers mathématique : en quête de la nature ultime du réel, Ekho, (EAN 978-2-10-077981-9).

Articles connexes
Liens externes
- Le Système international d'unités [PDF], Bureau international des poids et mesures, 9e éd., 2019, p. 19
- « Rœmer et la vitesse de la lumière », texte de Roemer sur le caractère fini de la vitesse de la lumière (1676) et commentaire sur BibNum (2009)
- « L'expérience du miroir tournant de Foucault », texte de la méthode de Foucault du miroir tournant (1853) et commentaire sur BibNum (2009)
- « "C" à Paris, Vitesse de la Lumière. Histoire et expériences », une exposition virtuelle de la Bibliothèque patrimoniale numérique de l'Observatoire de Paris
- « Mesurez la vitesse de la lumière avec du chocolat et un micro-ondes… », sur Futura (consulté le )
- Notices dans des dictionnaires ou encyclopédies généralistes :
- Portail de la physique
- Portail de l’optique
- Portail de l’astronomie