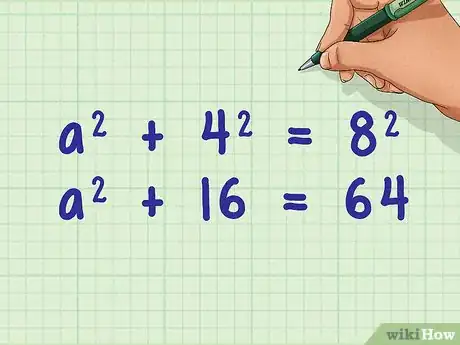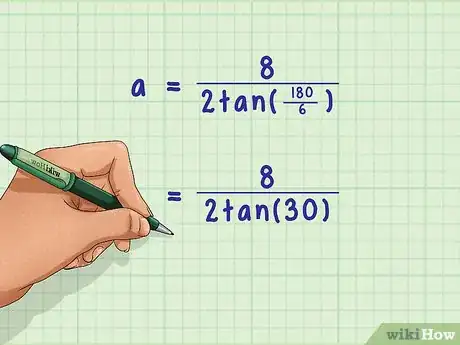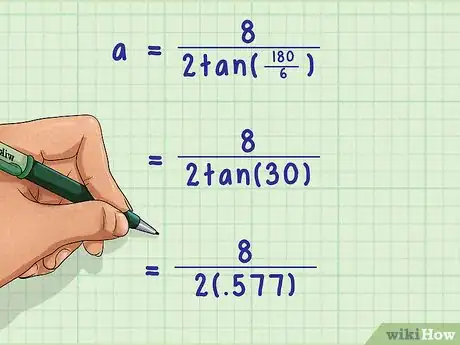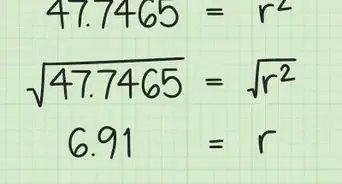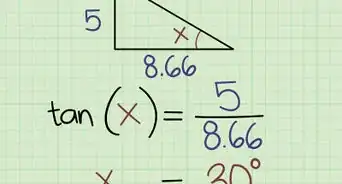This article was co-authored by wikiHow Staff. Our trained team of editors and researchers validate articles for accuracy and comprehensiveness. wikiHow's Content Management Team carefully monitors the work from our editorial staff to ensure that each article is backed by trusted research and meets our high quality standards.
There are 7 references cited in this article, which can be found at the bottom of the page.
This article has been viewed 228,667 times.
Learn more...
A hexagon is a six-sided polygon. When a hexagon is regular it has six equal side lengths and an apothem. An apothem is a line segment from the center of a polygon to the middle point of any one side. You usually need to know the length of the apothem when calculating the area of a hexagon.[1] As long as you know the side length of the hexagon, you can calculate the length of the apothem.
Steps
Using the Pythagorean Theorem (Given Side Length or Radius)
-
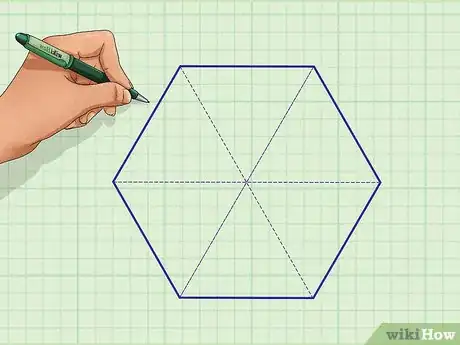
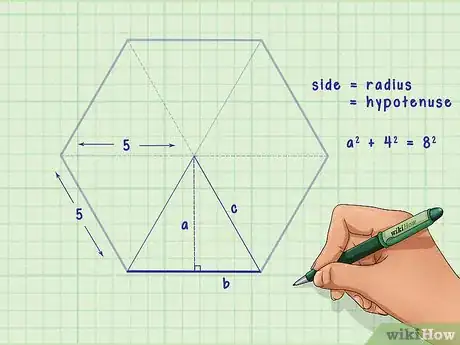
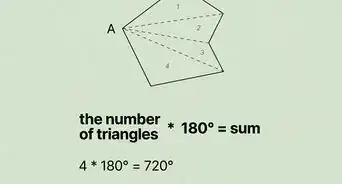
1Divide the hexagon into six congruent, equilateral triangles. To do this, draw a line connecting each vertex, or point, with the vertex opposite.[2]
-
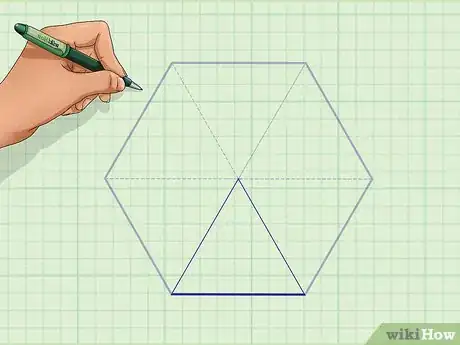
2Choose one triangle and label the length of its base. This is equal to the side length of the hexagon.[3]
- For example, you might have a hexagon with a side length of 8 cm. The base of each equilateral triangle, then, is also 8 cm.
Advertisement -
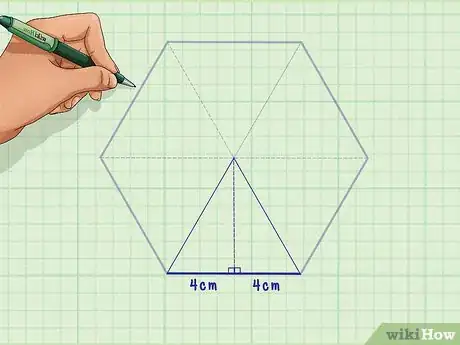
3Create two right triangles. To do this, draw a line from the top vertex of the equilateral triangle perpendicular to its base. This line will cut the base of the triangle in half (and thus is the apothem of the hexagon). Label the length of the base of one of the right triangles.[4]
- For example, if the base of the equilateral triangle is 8 cm, when you divide the triangle into two right triangles, each right triangle now has a base of 4 cm.
-
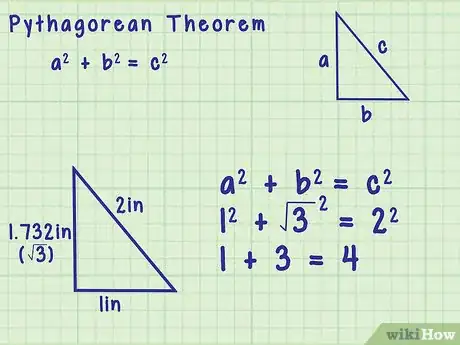
4Set up the formula for the Pythagorean Theorem. The formula is , where equals the length of the hypotenuse (the side opposite the right angle), and and equal the lengths of the other two sides of the triangle.
- For example, if a right triangle had a hypotenuse of inches, one leg of inch, and another leg of about inches (), the Pythagorean Theorem would state that , which is true when you complete the calculations: .
-
5Plug the length of the right triangle’s base into the formula. Substitute for .
- For example, if the length of the base is 4 cm, your formula will look like this: .
-
6Plug the length of the hypotenuse into the formula. You know the length of the hypotenuse because you know the side length of the hexagon. The side length of a regular hexagon is equal to the radius of the hexagon. The radius is a line that connects the central point of a polygon with one of its vertices.[5] You’ll note that the hypotenuse of your right triangle is also a radius of the hexagon, thus, the side length of the hexagon is equal to the length of the hypotenuse.
- For example, if the side length of the hexagon is 8 cm, then the length of the right triangle’s hypotenuse is also 8 cm. So your formula will look like this: .
-
7Square the known values in the formula. Remember that squaring a number means to multiply it by itself.
- For example, squaring the known values, your formula will look like this: .
-
8Isolate the unknown variable. To do this, subtract the squared value of from both sides of the equation.
- For example:
- For example:
-
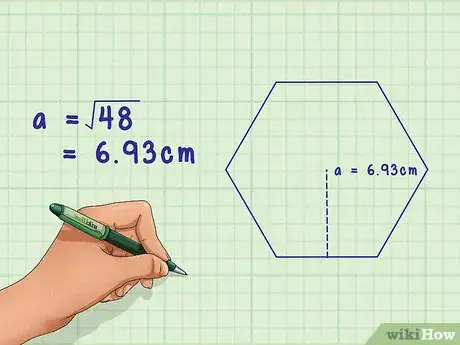
9Solve for . To do this, find the square root of each side of the equation. This will give you the length of the missing side of the triangle, which is equal to the length of the hexagon’s apothem.[6]
- For example, using a calculator, you can calculate . Thus, the missing length of the right triangle, and the length of the hexagon’s apothem, equals 6.93 cm.
Using Trigonometry (Given Side Length or Radius)
-
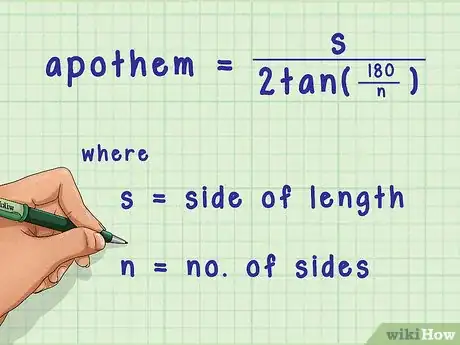
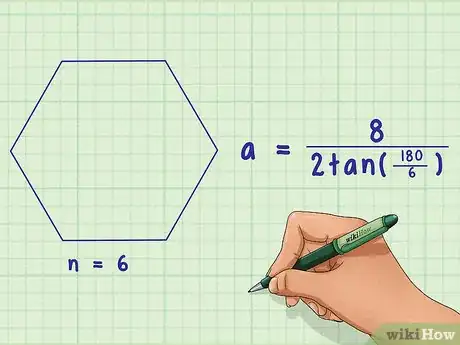
1Set up the formula for finding the apothem of a regular polygon. The formula is , where equals the side length of the polygon and equals the number of sides the polygon has.[7]
-
2Plug the side length into the formula. Remember to substitute for the variable .
- For example, for a hexagon with a side length of 8 cm, the formula will look like this: .
-
3Plug the number of sides into the formula. A hexagon has 6 sides. Remember to substitute for the variable .
- For example: .
-
4Complete the calculation in parentheses. You are finding the degrees you will use to calculate the tangent.[8]
- For example, , so the formula now look like this: .
-
5Find the tangent. To do this, use a calculator or a trigonometry table.[9]
- For example, the tangent of 30 is about .577, so the formula will now look like this: .
-
6Multiply the tangent by 2, then divide the side length by this number. This will give you the length of the apothem of your hexagon.[10]
- For example:
So, the apothem of a regular hexagon with 8-cm sides is about 6.93 cm.
- For example:
Community Q&A
-
QuestionIs there a formula to calculate the apothem if you only know how long one side of the hexagon is, and its perimeter?
 Community AnswerSince all you need to know to calculate the apothem is the length of one side of the hexagon, the length of the perimeter is irrelevant. Use the length of the side with any of the methods in the article.
Community AnswerSince all you need to know to calculate the apothem is the length of one side of the hexagon, the length of the perimeter is irrelevant. Use the length of the side with any of the methods in the article. -
QuestionIs there away to calculate perimeter of a hexagon by only the area?
 DonaganTop AnswererYes. When you know the area, set it equal to [(3√3) s²] / 2, where s is the length of a side. Solve the equation for s, and multiply that length by 6.
DonaganTop AnswererYes. When you know the area, set it equal to [(3√3) s²] / 2, where s is the length of a side. Solve the equation for s, and multiply that length by 6. -
QuestionWith Method two it metions it can also be used with the radius. However in the explanation it only shows side length. So would I use the same formula but use the radius instead of the side length?
 Pangdi XiongCommunity AnswerThe radius of a hexagon is the same as the side length, because the circle is inscribed in the hexagon. So just use the same formula and plug it in.
Pangdi XiongCommunity AnswerThe radius of a hexagon is the same as the side length, because the circle is inscribed in the hexagon. So just use the same formula and plug it in.
References
- ↑ https://www.mathsisfun.com/geometry/regular-polygons.html
- ↑ https://www.mechamath.com/geometry/apothem-of-a-hexagon-formulas-and-examples/
- ↑ https://www.mechamath.com/geometry/apothem-of-a-hexagon-formulas-and-examples/
- ↑ https://www.mechamath.com/geometry/apothem-of-a-hexagon-formulas-and-examples/
- ↑ https://www.mathsisfun.com/definitions/radius-polygon-.html
- ↑ https://www.mechamath.com/geometry/apothem-of-a-hexagon-formulas-and-examples/
- ↑ http://www.mathopenref.com/apothem.html
- ↑ https://www.varsitytutors.com/high_school_math-help/how-to-find-the-area-of-a-hexagon
- ↑ https://www.mathopenref.com/apothem.html
About This Article
To calculate the apothem of a hexagon, start by dividing the hexagon into 6 triangles. Then, divide one of the triangles in half to create 2 right triangles. Next, plug the length of one of the right triangle's base and hypotenuse into the Pythagorean Theorem. Finally, solve for a to get the apothem of the hexagon. To learn how to calculate the apothem of a hexagon using trigonometry, scroll down!