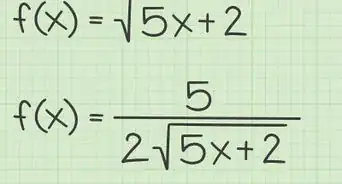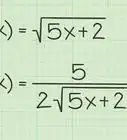How to Evaluate Multivariable Limits

1. 1
   Try directly substituting first. Sometimes, a limit is trivial to calculate - similar to single-variable calculus, plugging in the values may immediately net you the answer. This is usually the case when the limit does not approach the origin. An example follows.

   • ${\displaystyle {\begin{aligned}\lim _{(x,y)\to (4,5)}(x^{2}y^{3}-5xy^{2})&=(4)^{2}(5)^{3}-5(4)(5)^{2}\\&=1500\end{aligned}}}$
   • Another reason why substituting works here is that the function above is polynomial, and therefore is well-behaved across the reals for all ${\displaystyle x}$ and ${\displaystyle y.}$
2. 2
   Try substituting to make the limit single-variable when the substitution is obvious.

   • Evaluate ${\displaystyle \lim _{(x,y)\to (0,0)}{\frac {\ln(1-5x^{2}y^{2})}{12x^{2}y^{2}}}.}$
   • Substitute ${\displaystyle t=x^{2}y^{2}.}$
     • ${\displaystyle \lim _{t\to 0}{\frac {\ln(1-5t)}{12t}}}$
   • Use L'Hôpital's rule, as currently we get a ${\displaystyle {\frac {0}{0}}}$ if we evaluate too soon.
     • ${\displaystyle {\begin{aligned}\lim _{t\to 0}{\frac {\ln(1-5t)}{12t}}&=\lim _{t\to 0}{\frac {{\frac {1}{1-5t}}(-5)}{12}}\\&={\frac {-5}{12}}.\end{aligned}}}$
   Advertisement
3. 3
   If you suspect that the limit does not exist (DNE), show this by approaching from two different directions. As long as the limit either DNE or is different from these two directions, you are finished and the limit of the overall function DNE.

   • Evaluate ${\displaystyle \lim _{(x,y)\to (0,0)}{\frac {x^{2}-y^{2}}{x^{2}+y^{2}}}.}$
   • Approach from both sides vertically and horizontally. Set ${\displaystyle x=0}$ and ${\displaystyle y=0.}$
     • ${\displaystyle \lim _{(0,y)\to (0,0)}{\frac {x^{2}-y^{2}}{x^{2}+y^{2}}}=\lim _{(0,y)\to (0,0)}{\frac {(0)^{2}-y^{2}}{(0)^{2}+y^{2}}}=-1.}$
     • ${\displaystyle \lim _{(x,0)\to (0,0)}{\frac {x^{2}-y^{2}}{x^{2}+y^{2}}}=\lim _{(x,0)\to (0,0)}{\frac {x^{2}-(0)^{2}}{x^{2}+(0)^{2}}}=1.}$
   • Since the two limits are different, the limit DNE.
4. 4
   Convert to polar form. Multivariable limits are often easier when done in polar coordinates. In this case, ${\displaystyle x=r\cos \theta }$ and ${\displaystyle y=r\sin \theta .}$ Let’s see how this works.
Advertisement

Example 1

1. 1
   Evaluate the limit.

   • ${\displaystyle \lim _{(x,y)\to (0,0)}{\frac {xy^{2}}{x^{2}+y^{2}}}}$
2. 2
   Convert to polar.

   • ${\displaystyle \lim _{r\to 0}{\frac {r^{3}\cos \theta \sin ^{2}\theta }{r^{2}}}=\lim _{r\to 0}(r\cos \theta \sin ^{2}\theta )}$
3. 3
   Use the Squeeze Theorem. Although the limit is taken as ${\displaystyle r\to 0,}$ the limit depends on ${\displaystyle \theta }$ as well. One might then naively conclude that the limit DNE. However, the limit does depend on ${\displaystyle r,}$ so the limit may or may not exist.

   • Since ${\displaystyle |\sin \theta |\leq 1}$ and ${\displaystyle |\cos \theta |\leq 1,|\cos \theta \sin ^{2}\theta |\leq 1}$ as well.
   • Then ${\displaystyle |r\cos \theta \sin ^{2}\theta |\leq r.}$
4. 4
   Take the limit of all three expressions.

   • Since ${\displaystyle \lim _{r\to 0}(-r)=\lim _{r\to 0}(r)=0,}$ by the Squeeze Theorem, ${\displaystyle \lim _{r\to 0}(r\cos \theta \sin ^{2}\theta )=0.}$
   • Because of the ${\displaystyle r}$ dependency and the use of the Squeeze Theorem, the quantity in the above limit is said to be bounded. In other words, as ${\displaystyle r\to 0,}$ the range of values of ${\displaystyle r\cos \theta \sin ^{2}\theta }$ shrinks to 0 as well, even though ${\displaystyle \theta }$ is arbitrary.
Advertisement

Example 2

1. 1
   Evaluate the limit.

   • ${\displaystyle \lim _{(x,y)\to (0,0)}{\frac {xy}{x^{2}+y^{2}}}}$
   • This example is only slightly different from the one in Example 1.
2. 2
   Convert to polar.

   • ${\displaystyle \lim _{r\to 0}{\frac {r^{2}\cos \theta \sin ^{2}\theta }{r^{2}}}=\lim _{r\to 0}(\cos \theta \sin ^{2}\theta )}$
   • However, the quantity ${\displaystyle \cos \theta \sin ^{2}\theta }$ can take on an arbitrary value after the limit is evaluated, and is said to be unbounded.
   • Therefore, the limit DNE. This scenario is describing a limit being approached from arbitrary directions and getting different values.
Advertisement