This article was co-authored by David Jia and by wikiHow staff writer, Jennifer Mueller, JD. David Jia is an Academic Tutor and the Founder of LA Math Tutoring, a private tutoring company based in Los Angeles, California. With over 10 years of teaching experience, David works with students of all ages and grades in various subjects, as well as college admissions counseling and test preparation for the SAT, ACT, ISEE, and more. After attaining a perfect 800 math score and a 690 English score on the SAT, David was awarded the Dickinson Scholarship from the University of Miami, where he graduated with a Bachelor’s degree in Business Administration. Additionally, David has worked as an instructor for online videos for textbook companies such as Larson Texts, Big Ideas Learning, and Big Ideas Math.
This article has been viewed 1,688,310 times.
If you're stuck on your geometry homework trying to figure out the area of a quadrilateral, you've come to the right place! Remember—the "area" of a shape is just how much 2-dimensional space it takes up. For some quadrilaterals, there's a handy formula you can use to calculate the area. But what if all the sides are different? Just divide it into triangles! Read on to follow along with some examples and see how this works.
Things You Should Know
- Find the area of any quadrilateral by dividing it into 2 triangles. Then, find the area of each of those triangles using the formula (Area = 1/2 base times height) and add them together.
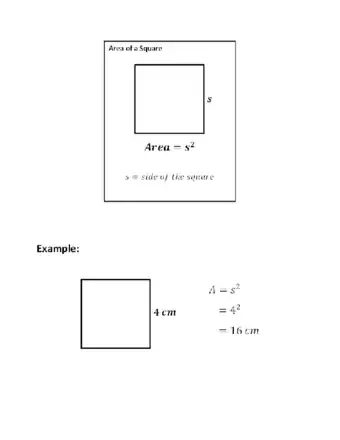
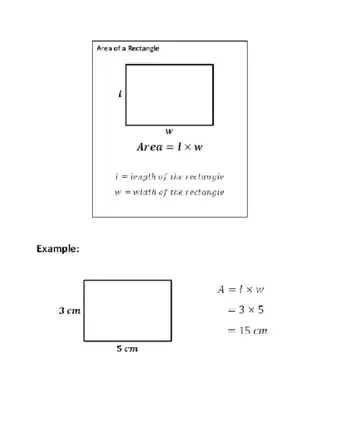
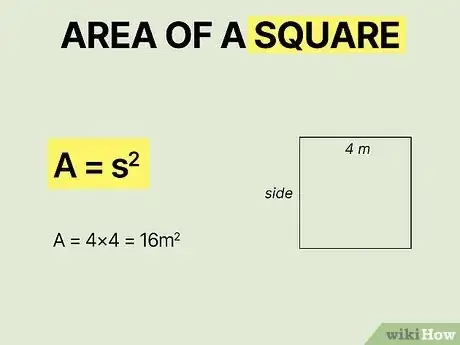
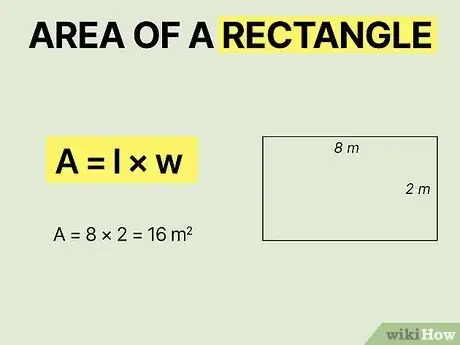
- Use the formula (Area = length times width) to find the area of a square or rectangle.
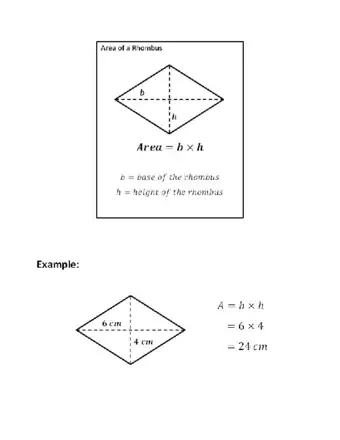
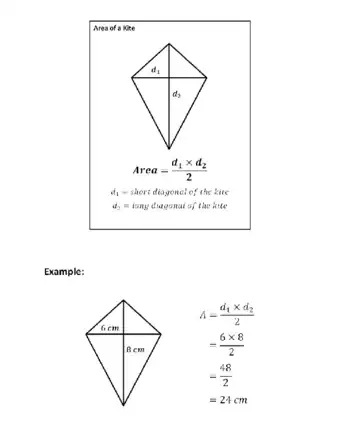
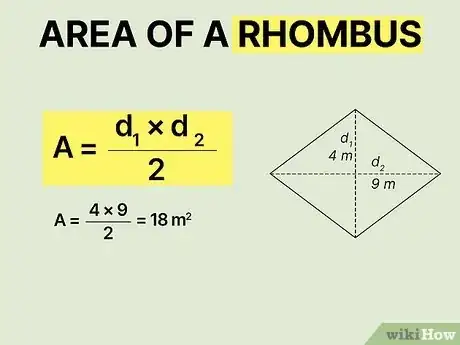
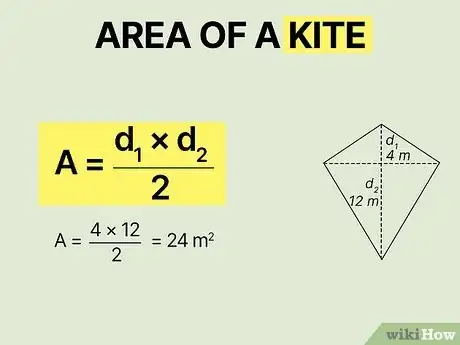
- Multiply the lengths of the 2 diagonal lines and divide by 2 to find the area of a rhombus or kite.
- Give the area of any quadrilateral in units squared. The unit corresponds with the unit used for the lengths you multiplied to find the area.
Steps
Area of Square, Rectangle, and Rhombus Cheat Sheets
Area of Trapezoid and Kite Cheat Sheets
Any Quadrilateral Shape
-
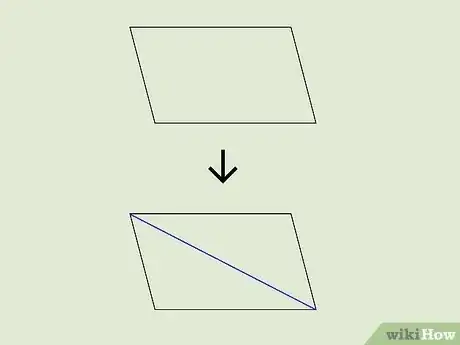
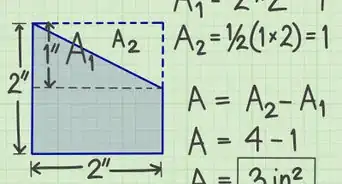
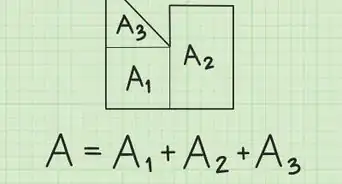
1Divide the quadrilateral into 2 triangles. If you draw a diagonal line from one corner to the other, you create 2 triangles within the quadrilateral. The 2 triangles might not be the same size, but they share a common base—the diagonal that divides the quadrilateral.[4]
- If you're working on a homework problem, the diagonal line might already be drawn for you. In fact, if you have a quadrilateral with a diagonal line, that's a pretty big clue that you'll use triangles to find the area.
-
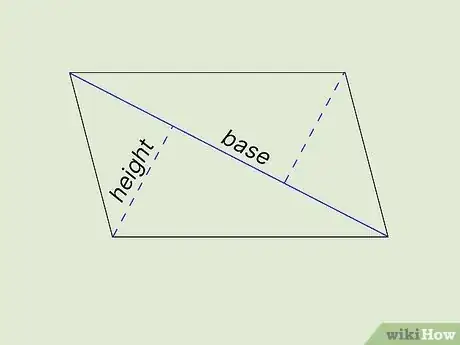
2Get the measurements for the base and heights of your triangles. To find the area of a triangle, you need to know the size of the base (b) and the height (h). Your diagonal line is serving as the base of your triangles, so they'll both have the same measurement for the base. They might not be the same height, though, depending on the quadrilateral. The height isn't the length of a side (unless you're working with a right triangle). It's the length from the base to the top point of the triangle.[5]
- If you're working a problem for homework and you're not given any way to measure these values, you can't use triangles to find the area of that quadrilateral.
-
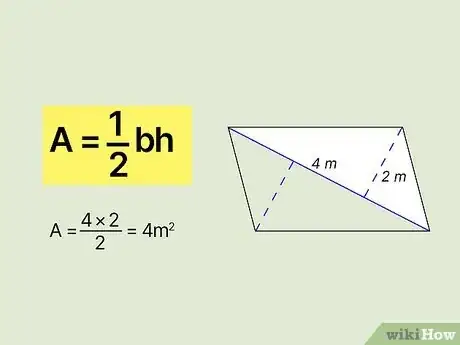
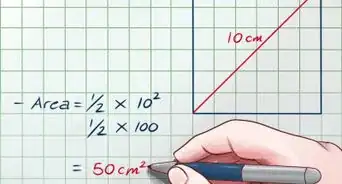
3Find the area of each triangle. Recall that the formula for the area of a triangle is . All you have to do is plug in the measurements you got for the base and the height, then simplify the equation to find the area of each triangle.[6]
- For example, say you have a diagonal with a length of that forms 2 triangles that each have a height of . Your formula would be , which simplifies to . So your answer would be .
- In this example, both triangles have the same area since they both have the same base and height.
-
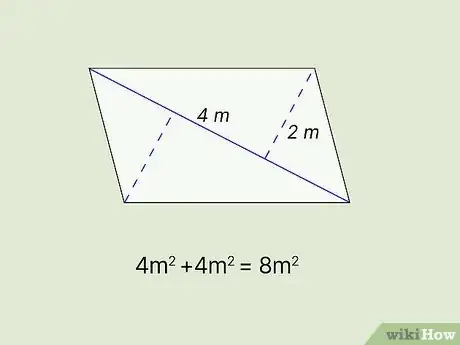
4Add the areas of the 2 triangles together to get the area of the quadrilateral. Since you originally divided your quadrilateral into 2 triangles, all you have to do is add those 2 areas together and you'll have the total area of the quadrilateral. You could also think of the area of one of the triangles as being half the area of the quadrilateral.[7]
- To return to the previous example, since each triangle has an area of , you would simply add to get .
- Area is always expressed in square units. If the measurements in your original problem were meters, your answer would be .
Community Q&A
-
QuestionCould I divide the quadrilateral into two triangles, find the area of each, and add them to find the area of the quadrilateral?
 DonaganTop AnswererYes. If you know the base and height of each triangle, you can just add the two areas together. It's not always possible, however, to know the bases and heights.
DonaganTop AnswererYes. If you know the base and height of each triangle, you can just add the two areas together. It's not always possible, however, to know the bases and heights. -
QuestionHow do I calculate the area of a parallelogram?
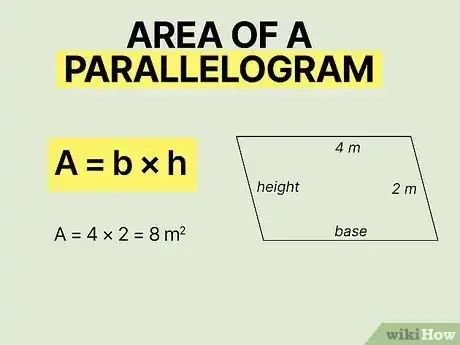
 Community AnswerCalculate as follows: Area = base multiplied by height.
Community AnswerCalculate as follows: Area = base multiplied by height. -
QuestionHow would I know the angle for quadrilateral?
 DonaganTop AnswererAssuming you're not given the angle(s), you either have to use a protractor or analyze the quadrilateral and use trigonometry.
DonaganTop AnswererAssuming you're not given the angle(s), you either have to use a protractor or analyze the quadrilateral and use trigonometry.
References
- ↑ https://flexbooks.ck12.org/cbook/ck-12-interactive-middle-school-math-6-for-ccss/section/9.3/related/lesson/find-the-dimensions-and-area-of-quadrilaterals-msm8/
- ↑ https://content.nroc.org/DevelopmentalMath/COURSE_TEXT2_RESOURCE/U07_L2_T2_text_final.html
- ↑ https://www.ck12.org/section/area-of-rhombus-and-kite/
- ↑ https://www.bbc.co.uk/bitesize/guides/z2ctyrd/revision/4
- ↑ https://www.bbc.co.uk/bitesize/guides/z2ctyrd/revision/4
- ↑ https://www.open.edu/openlearn/science-maths-technology/mathematics-statistics/geometry/content-section-3.1
- ↑ https://www.bbc.co.uk/bitesize/guides/z2ctyrd/revision/4
About This Article
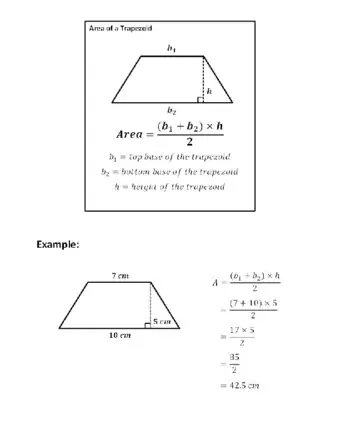
Before you can find the area of a regular quadrilateral, start by identifying the type of quadrilateral in the problem, since different types of quadrilaterals require different equations. For rectangles or rhombuses, simply multiply the base by the height to find the area. For squares, multiply one side by itself to get the area. If you have a parallelogram, multiply the diagonals and divide by 2 to get the area. To find the area of a trapezoid, add the base and the height together, and divide that number by 2 times the height. If you want to find the area of an irregular quadrilateral, keep reading the article!