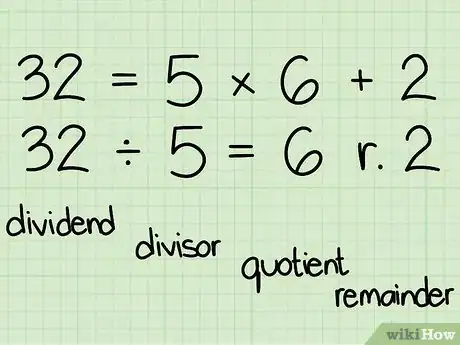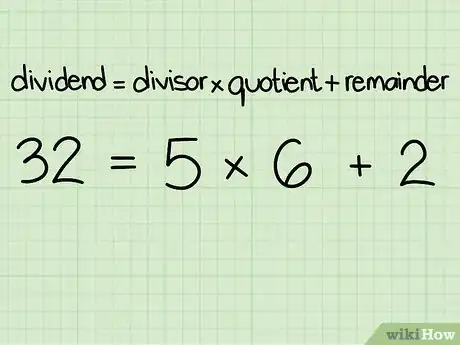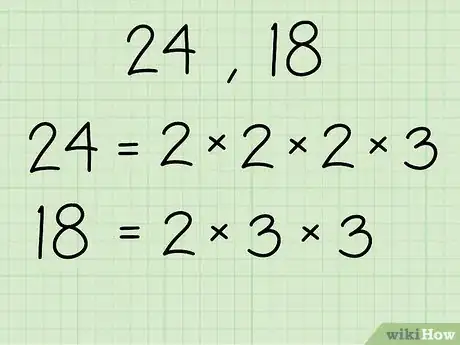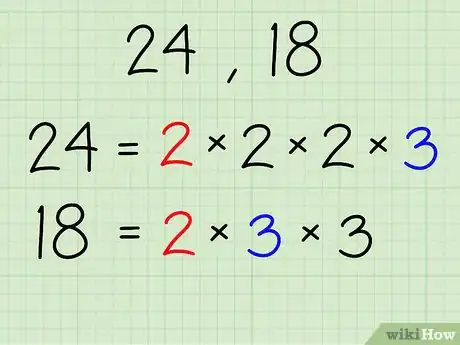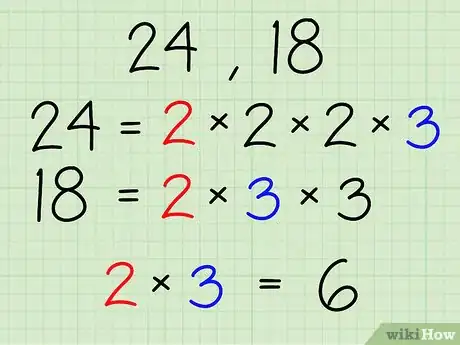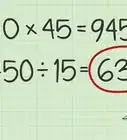wikiHow is a “wiki,” similar to Wikipedia, which means that many of our articles are co-written by multiple authors. To create this article, 40 people, some anonymous, worked to edit and improve it over time.
This article has been viewed 599,363 times.
Learn more...
The Greatest Common Divisor (GCD) of two whole numbers, also called the Greatest Common Factor (GCF) and the Highest Common Factor (HCF), is the largest whole number that's a divisor (factor) of both of them. For instance, the largest number that divides into both 20 and 16 is 4. (Both 16 and 20 have larger factors, but no larger common factors -- for instance, 8 is a factor of 16, but it's not a factor of 20.) In grade school, most people are taught a "guess-and-check" method of finding the GCD. Instead, there is a simple and systematic way of doing this that always leads to the correct answer. The method is called "Euclid's algorithm." If you want to know how to truly find the Greatest Common Divisor of two integers, see Step 1 to get started.[1]
Steps
Using the Divisor Algorithm
-
1Drop any negative signs.
-
2Know your vocabulary: when you divide 32 by 5,[2]
- 32 is the dividend
- 5 is the divisor
- 6 is the quotient
- 2 is the remainder (or modulo).
Advertisement -
3Identify the larger of the two numbers. That will be the dividend, and the smaller the divisor.[3]
-
4Write out this algorithm: (dividend) = (divisor) * (quotient) + (remainder)[4]
-
5Put the larger number in the spot for dividend, and the smaller number as the divisor.[5]
-
6Decide how many times the smaller number will divide into the larger number, and drop it into the algorithm as the quotient.
-
7Calculate the remainder, and substitute it into the appropriate place in the algorithm.[6]
-
8Write out the algorithm again, but this time A) use the old divisor as the new dividend and B) use the remainder as the new divisor.
-
9Repeat the previous step until the remainder is zero.
-
10The last divisor is the greatest common divisor.
-
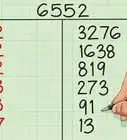
11Here is an example, where we are trying to find the GCD of 108 and 30:
-
12Notice how the 30 and the 18 in the first line shift positions to create the second line. Then, the 18 and 12 shift to create the third line, and the 12 and 6 shift to create the fourth line. The 3, 1, 1, and 2 that follow the multiplication symbol do not reappear. They represent how many times the divisor goes into the dividend, so they are unique to each line.
Using Prime Factors
-
1Drop any negative signs.[7]
-
2Find the prime factorization of the numbers, and list them out as shown.[8]
- Using 24 and 18 as the example numbers:
- 24- 2 x 2 x 2 x 3
- 18- 2 x 3 x 3
- Using 50 and 35 as the example numbers:
- 50- 2 x 5 x 5
- 35- 5 x 7
- Using 24 and 18 as the example numbers:
-
3Identify all common prime factors.
- Using 24 and 18 as the example numbers:
- 24- 2 x 2 x 2 x 3
- 18- 2 x 3 x 3
- Using 50 and 35 as the example numbers:
- 50- 2 x 5 x 5
- 35- 5 x 7
- Using 24 and 18 as the example numbers:
-
4
-
5Finished.
Community Q&A
-
QuestionHow do I find the gcd of three integers?
 DonaganTop AnswererFind all of the divisors of each of the integers, and note the largest one that's common to all three.
DonaganTop AnswererFind all of the divisors of each of the integers, and note the largest one that's common to all three. -
QuestionHow do I round off 93,678,563 to the nearest 10,000?
 DonaganTop AnswererLook at the digit in the 1,000's place: it's 8, so you round up to 93,680,000.
DonaganTop AnswererLook at the digit in the 1,000's place: it's 8, so you round up to 93,680,000. -
QuestionWhat is a multiplicative inverse?
 DonaganTop AnswererA multiplicative inverse is the reciprocal of a number.
DonaganTop AnswererA multiplicative inverse is the reciprocal of a number.
References
- ↑ https://brilliant.org/wiki/greatest-common-divisor/
- ↑ https://www.math-only-math.com/dividend-divisor-quotient-and-remainder.html
- ↑ http://sites.math.rutgers.edu/~greenfie/gs2004/euclid.html
- ↑ http://sites.math.rutgers.edu/~greenfie/gs2004/euclid.html
- ↑ https://www.youtube.com/watch?v=h86RzlyHfUE
- ↑ https://www.youtube.com/watch?v=h86RzlyHfUE
- ↑ https://www.sparknotes.com/math/prealgebra/wholenumbers/section4/
- ↑ https://www.sparknotes.com/math/prealgebra/wholenumbers/section4/
- ↑ https://www.youtube.com/watch?v=25QB-JjZLxY