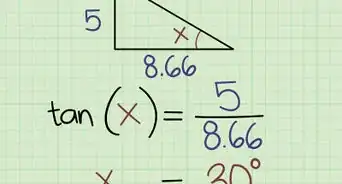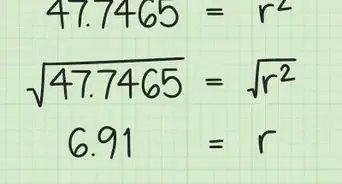This article was co-authored by wikiHow staff writer, Hannah Madden. Hannah Madden is a writer, editor, and artist currently living in Portland, Oregon. In 2018, she graduated from Portland State University with a B.S. in Environmental Studies. Hannah enjoys writing articles about conservation, sustainability, and eco-friendly products. When she isn’t writing, you can find Hannah working on hand embroidery projects and listening to music.
This article has been viewed 91,235 times.
Learn more...
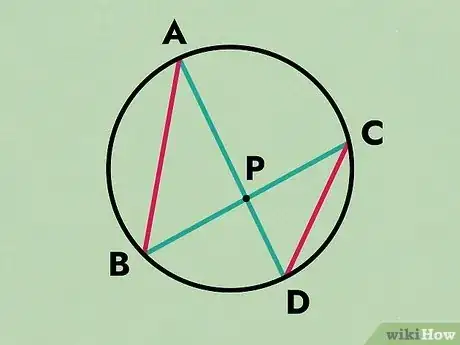
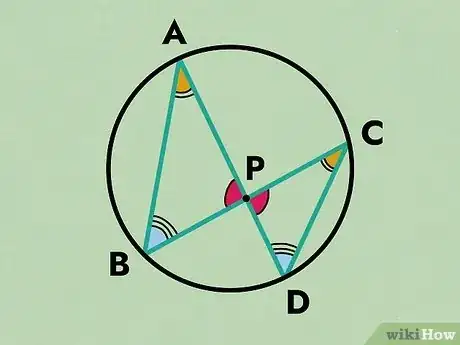
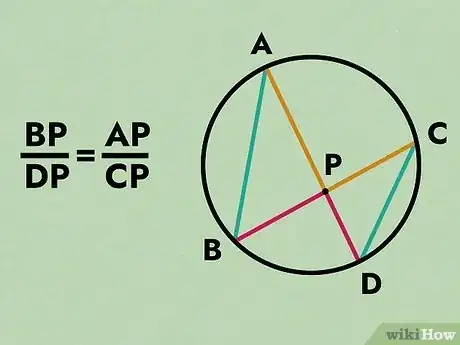
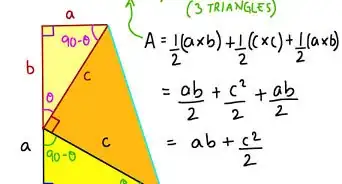
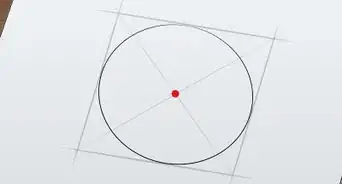
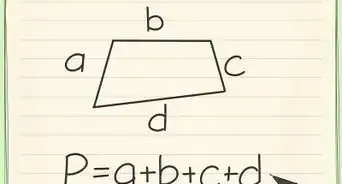
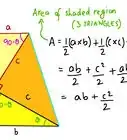
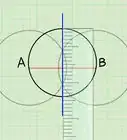
In geometry, the Intersecting Chords Theorem of Euclid is a statement that describes the relationship between 4 line segments created by 2 intersecting chords in a circle. Euclid’s theorem states that the products of the lengths of the line segments on each chord are equal. You can prove this mathematically with a few simple steps and a diagram. Keep reading to learn how to prove the Intersecting Chords Theorem of Euclid.
Steps
References
- ↑ http://www2.fairmontstate.edu/users/ywang/teaching/fsu/courses/geometry_372/lecture_372_ch4.pdf
- ↑ https://www.spps.org/cms/lib/MN01910242/Centricity/Domain/853/IBFMathHLGeom.pdf
- ↑ https://amsi.org.au/teacher_modules/Circle_Geometry.html
- ↑ https://amsi.org.au/teacher_modules/Circle_Geometry.html
- ↑ http://www2.fairmontstate.edu/users/ywang/teaching/fsu/courses/geometry_372/lecture_372_ch4.pdf