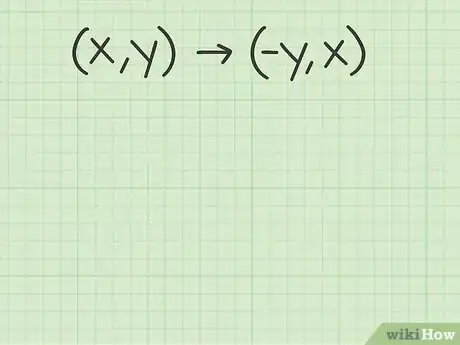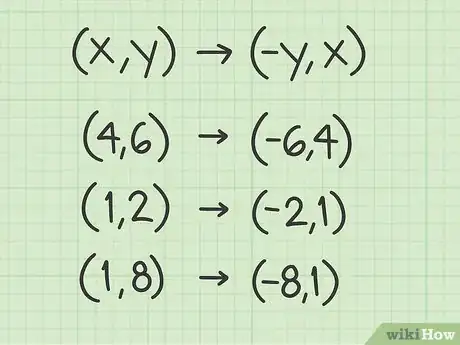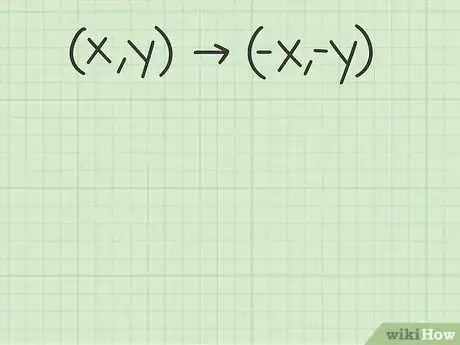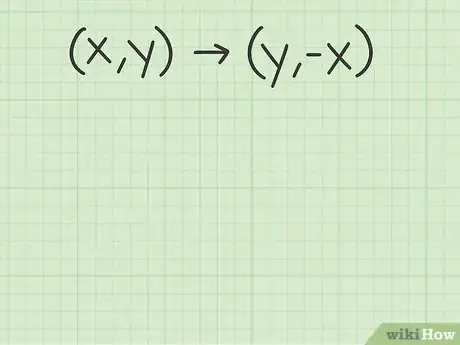How to Rotate a Shape

Co-authored by wikiHow Staff

Last Updated: December 13, 2022 References Approved

A rotation is a type of geometrical transformation in which the vertices of a shape are rotated at a certain angle around a fixed point (called the center of rotation).^{[1]
X
Research source} In simpler terms, imagine gluing a triangle to the second hand of a clock that is spinning backwards. Usually, you will be asked to rotate a shape around the origin, which is the point (0, 0) on a coordinate plane. You can rotate shapes 90, 180, or 270 degrees around the origin using three basic formulas.

Method 1

Method 1 of 3:

Rotating a Shape 90 Degrees About the Origin

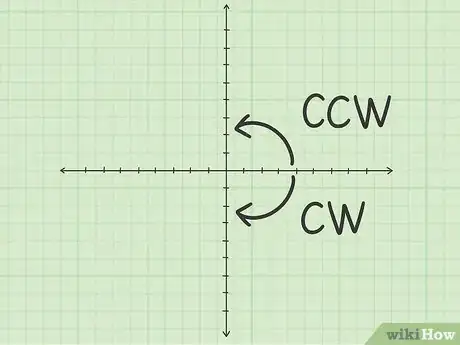
1
Note the corresponding clockwise and counterclockwise rotations. Rotating a shape 90 degrees is the same as rotating it 270 degrees clockwise.^{[2]
X
Research source}The convention is that when rotating shapes on a coordinate plane, they rotate counterclockwise, or towards the left.^{[3]
X
Research source} You should assume this, unless it is noted in the problem that you need to rotate clockwise.
- For example, if the problem states, “Rotate the shape 90 degrees around the origin,” you can assume you are rotating the shape counterclockwise.
  - You would complete this problem the same way you complete a problem that asks “Rotate the shape 270 degrees clockwise around the origin.”
  - You might also see, “Rotate this shape -270 degrees around the origin.”
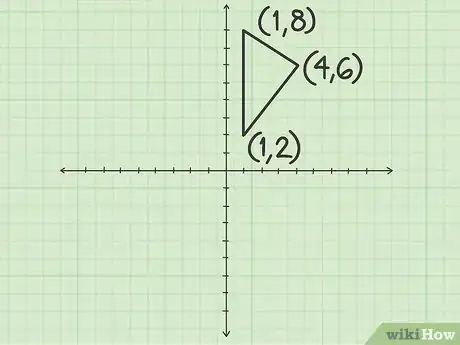
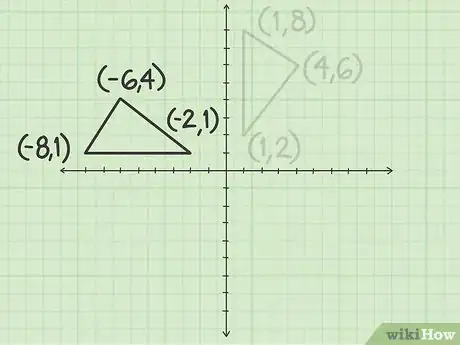
2
Find the coordinates of the original vertices. If these aren’t already provided, determine the coordinates using the graph. Remember that coordinates of points are shown using the $(x,y)$ $(x,y)$ formula, where $x$ $x$ equals the point on the horizontal, or x-axis, and $y$ $y$ equals the point on the vertical, or y-axis.^{[4]
X
Research source}
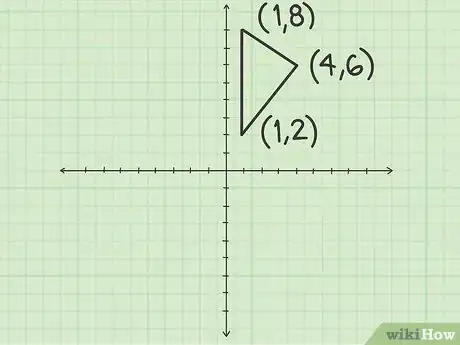
- For example, you might have a triangle with points (4, 6), (1, 2), and (1, 8).
Advertisement
3
Set up the formula for rotating a shape 90 degrees. The formula is $(x,y)\rightarrow (-y,x)$ .^{[5]
X
Research source} This formula shows that you are reflecting the shape, then flipping it.^{[6]
X
Research source}
4
Plug the coordinates into the formula. Make sure that you keep your x and y-coordinates straight. In this formula, you take the negative of the y value, and then switch the order of the coordinates.^{[7]
X
Research source}
- For example, the points (4, 6), (1, 2), and (1, 8) become (-6, 4), (-2, 1), and (-8, 1).
5
Draw the new shape. Plot the new vertex points on the plane. Connect your points using a straightedge. The resulting shape shows the original shape rotated 90 degrees around the origin.^{[8]
X
Research source}

Advertisement

Method 2

Method 2 of 3:

Rotating a Shape 180 Degrees About the Origin

1
Identify the corresponding clockwise and counterclockwise rotations. Since a full rotation has 360 degrees, rotating a shape 180 degrees clockwise is the same as rotating 180 counterclockwise.
- If the problem states, “Rotate the shape 180 degrees around the origin,” you can assume you are rotating the shape counterclockwise.
  - You would complete this problem the same way you complete a problem that asks “Rotate the shape 180 degrees clockwise around the origin.”
  - You might also see, “Rotate this shape -180 degrees around the origin.”
2
Write down the coordinates of the original shape’s vertices. These will likely be given. If not, you should be able to deduce them from looking at the coordinate graph. Remember to note the coordinates of each vertex’s point using the (x, y) convention.
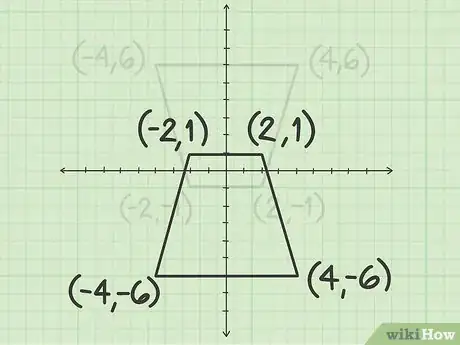
- For example, you might have a rhombus with points (4, 6), (-4, 6), (-2, -1), and (2, -1).
3
Set up the formula for rotating a shape 180 degrees. The formula is $(x,y)\rightarrow (-x,-y)$ .^{[9]
X
Research source} This formula shows that you are reflecting the shape twice.^{[10]
X
Research source}
4
Plug the coordinates into the formula. Take care to plug the correct coordinate into the correct position of the new ordered pair. In this formula, you keep the x and y values in the same position, but you take the negative value of each coordinate.
- For example, the points (4, 6), (-4, 6), (-2, -1), and (2, -1) become (-4, -6), (4, -6), (2, 1), and (-2, 1).
5
Draw the new shape. Plot the new vertex points on the plane. Connect your points using a straightedge. The resulting shape shows the original shape rotated 180 degrees around the origin.^{[11]
X
Research source}

Advertisement

Method 3

Method 3 of 3:

Rotating a Shape 270 Degrees About the Origin

1
Note the corresponding clockwise and counterclockwise rotations. Rotating a shape 270 degrees is the same as rotating it 90 degrees clockwise. Conventionally, shapes are rotated counterclockwise on a coordinate plane.^{[12]
X
Research source} You should assume this, unless it is noted in the problem that you need to rotate clockwise.
- For example, if the problem states, “Rotate the shape 270 degrees around the origin,” you can assume you are rotating the shape counterclockwise.
  - You would complete this problem the same way you complete a problem that asks “Rotate the shape 90 degrees clockwise around the origin.”
  - You might also see, “Rotate this shape -90 degrees around the origin.”
2
Find the coordinates of the original vertices. This information should be provided, or you should be able to easily find the coordinates by looking at the coordinate plane.
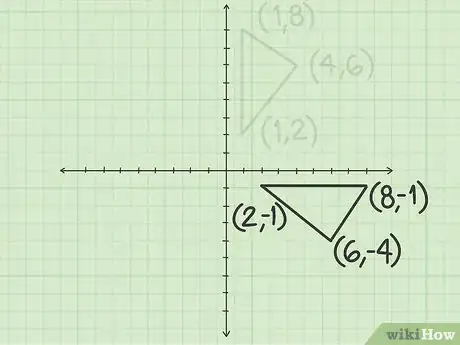
- For example, you might have a triangle with points (4, 6), (1, 2), and (1, 8).
3
Set up the formula for rotating a shape 270 degrees. The formula is $(x,y)\rightarrow (y,-x)$ .^{[13]
X
Research source} It shows you that are reflecting the shape, then flipping it.^{[14]
X
Research source}
4
Plug the coordinates into the formula. Make sure you plug the correct x and y values into the new coordinate pair. In this formula, the x and y values are reversed, and you take the negative value of the x coordinate.^{[15]
X
Research source}
- For example, the points (4, 6), (1, 2), and (1, 8) become (6, -4), (2, -1), and (8, -1).
5
Draw the new shape. Draw the new points on the plane. Use a straightedge to connect them. The resulting shape shows the original shape rotated 270 degrees around the origin.^{[16]
X
Research source}

Advertisement

Community Q&A

Question

How would I rotate a quadrilateral about a point?

Nitakuar

Community Answer

If the point is the origin, then simply apply above the transformation for each of the vertices. If it is some other point, then shift the coordinate axes parallel to the original so it becomes the origin and, after rotation, revert back to the original coordinates.
Question

What does "around the origin" mean? Does it mean around point (0,0)?

Community Answer

The origin is around (0,0), the center of the diagram.
Question

What if the number is negative?

Donagan

Top Answerer

If we assume a positive rotation is counterclockwise (anti-clockwise), a negative rotation would be clockwise (to the right at the top).

Advertisement

You Might Also Like

Advertisement

References

More References (7)

About This Article

Co-authored by:

wikiHow Staff Writer

This article was co-authored by wikiHow Staff. Our trained team of editors and researchers validate articles for accuracy and comprehensiveness. wikiHow's Content Management Team carefully monitors the work from our editorial staff to ensure that each article is backed by trusted research and meets our high quality standards. This article has been viewed 151,482 times.

126 votes - 71%

Co-authors: 15

Updated: December 13, 2022

Views: 151,482

Categories: Geometry

Article SummaryX

To rotate a shape 90 degrees around the point of origin, turn the x and y coordinates into -y and +x coordinates. For example, a triangle with the coordinates 1,2, 4,2, and 4,4 would become -2,1, -2,4, and -4,4. If you want to rotate a shape 180 degrees around the point of origin, turn the x and y coordinates into -y and -x coordinates. So, if a line has the coordinates 2,4 and 4,5, it would rotate to -4,-2 and -5,-4. Read more to learn how to rotate a shape 270 degrees!

Did this summary help you?

Advertisement