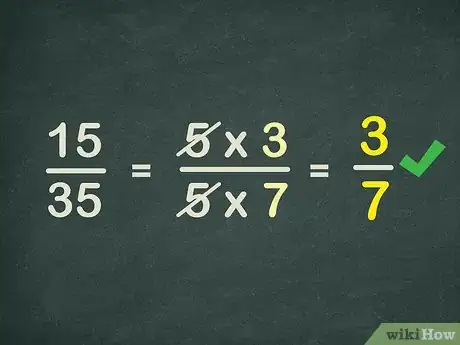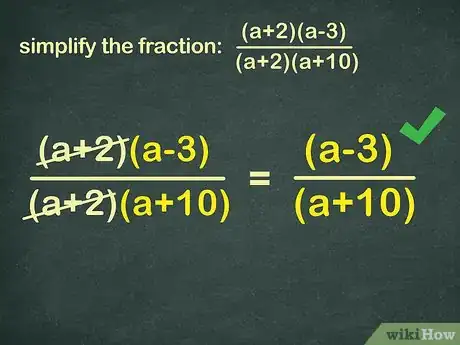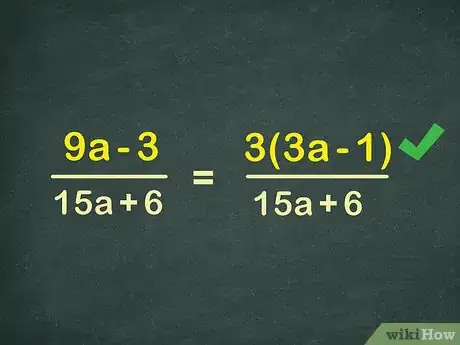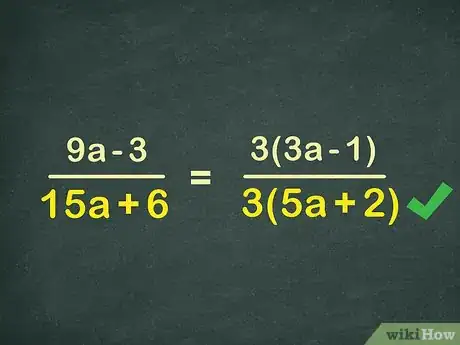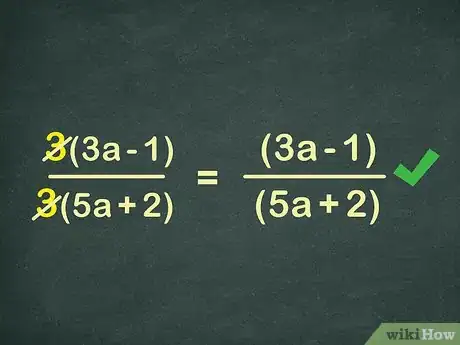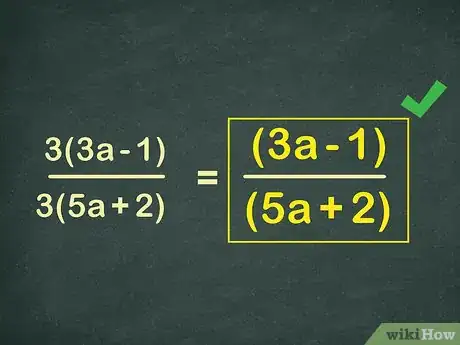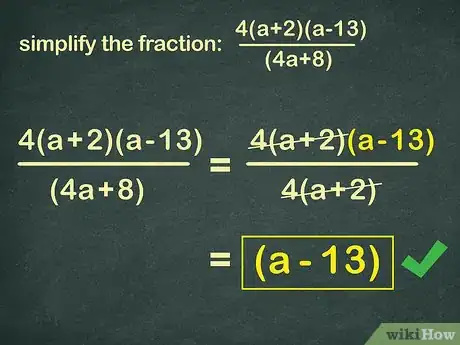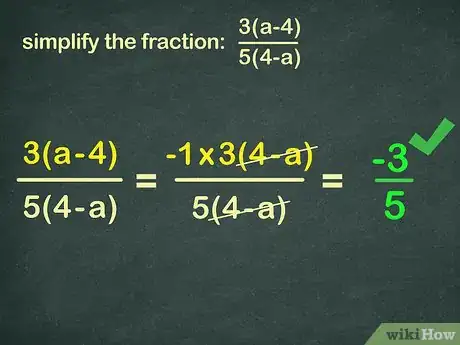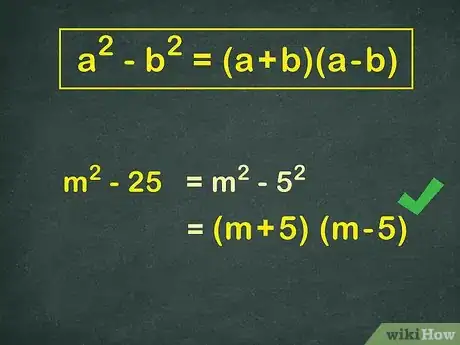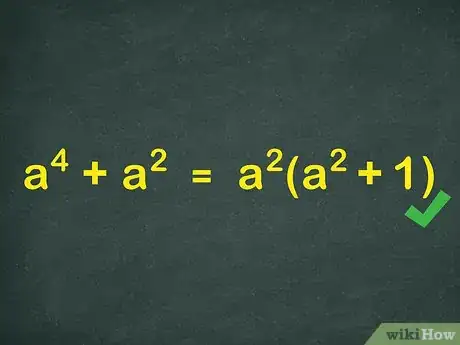How to Simplify Algebraic Fractions

Co-authored by David Jia

Last Updated: December 5, 2022 References

Algebraic fractions look incredibly difficult at first, and can seem daunting to tackle for the untrained student. With a mixture of variables, numbers, and even exponents, it is hard to know where to begin. Luckily however, the same rules needed to simplify regular fractions, like 15/25, still apply to algebraic fractions.

Method 1

Method 1 of 3:

Simplifying Fractions

1
Know the vocabulary for algebraic fractions. The following terms will be used throughout the examples, and are common in problems involving algebraic fractions:^{[1]
X
Research source}
- Numerator: The top part of a fraction (ie. (x+5)/(2x+3)).
- Denominator: The bottom part of the fraction (ie. (x+5)/(2x+3)).
- Common Denominator: This is a number that you can divide out of both the top and bottom of a fraction. For example, in the fraction 3/9, the common denominator is 3, since both numbers can be divided by 3.
- Factor: One number that multiples to make another. For example, the factors of 15 are 1, 3, 5, and 15. The factors of 4 are 1, 2, and 4.
- Simplified Equation: This involves removing all common factors and grouping similar variables together (5x + x = 6x) until you have the most basic form of a fraction, equation, or problem. If you cannot do anything more to the fraction, it is simplified.
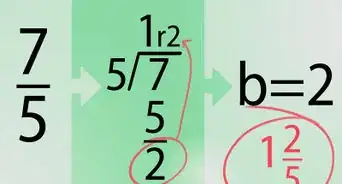
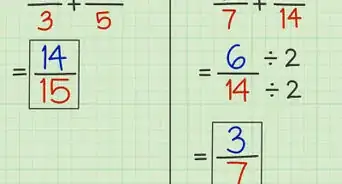
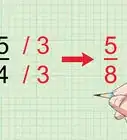
2
Review how to solve simple fractions. These are the exact same steps you will take to solve algebraic fractions.^{[2]
X
Research source} Take the example, 15/35. In order to simplify a fraction, we need to find a common denominator. In this case, both numbers can be divided by five, so you can remove the 5 from the fraction:
15 → 5 * 3
35 → 5 * 7
Now you can cross out like terms. In this case you can cross out the two fives, leaving your simplified answer, 3/7.

Advertisement
3
Remove factors from algebraic expressions just like normal numbers.^{[3]
X
Research source} In the previous example, you could easily remove the 5 from 15, and the same principle applies to more complex expressions like, 15x – 5. Find a factor that both numbers have in common. Here, the answer is 5, since you can divide both 15x and -5 by the number five. Like before, remove the common factor and multiply it by what is “left.”
15x – 5 = 5 * (3x – 1) To check your work, simply multiply the five back into the new expression – you will end up with the same numbers you started with.
4
Know you can remove complex terms just like simple ones. The same principle used in common fractions works for algebraic ones as well. This is the easiest way to simplify fractions while you work.^{[4]
X
Research source} Take the fraction:
(x+2)(x-3)
(x+2)(x+10)
Notice how the term (x+2) is common in both the numerator (top) and denominator (bottom). As such, you can remove it to simplify the algebraic fraction, just like you removed the 5 from 15/35:
~~(x+2)~~(x-3) → (x-3)
~~(x+2)~~(x+10) → (x+10) This leaves us with our final answer: (x-3)/(x+10)

Method 2

Method 2 of 3:

Simplifying Algebraic Fractions

1
Find a common factor in the numerator, or top part of the fraction. The first thing to do when simplifying an algebraic fraction is to simplify each part of the fraction. Start with the top part, factoring out as many numbers as you can.^{[5]
X
Research source} For an example, this section will use the problem:
9x-3
15x+6
Start with the numerator: 9x – 3. There is a common factor to both 9x and -3: 3. Factor out the 3 like you would any other number, leaving you with 3 * (3x-1). This is your new numerator:
3(3x-1)
15x+6
2
Find a common factor in the denominator.^{[6]
X
Research source} Continuing the example from above, isolate the denominator, 15x+6. Again, look for a number that can divide into both parts. Here you can again factor out a 3, leaving you with 3 * (5x +2). Write in your new denominator:
3(3x-1)
3(5x+2)
3
Remove like terms. This is the stage where you really get to simplify the fraction. Take any terms that are in both the numerator and the denominator and remove them. In this case, we can remove the 3 from both the top and the bottom.^{[7]
X
Research source}
3(3x-1) → (3x-1)
3(5x+2) → (5x+2)
4
Know when the equation is fully simplified. A fraction is simplified when there are no more common factors in the top or the bottom.^{[8]
X
Research source} Remember that you cannot remove factors from inside the parenthesis – in the example problem you cannot factor out the x from 3x and 5x, since the full terms are actually (3x -1) and (5x + 2). Thus, the example is fully simplified, making the final answer:
(3x-1)
(5x+2)
5
Try a practice problem. The best way to learn is to keep trying to simplify algebraic fractions. The answers are underneath the problems.
4(x+2)(x-13)
(4x+8) Answer: (x=13)
2x²-x
5x Answer:(2x-1)/5

Method 3

Method 3 of 3:

Tricks for Difficult Problems

1
”Reverse” parts of the fraction by factoring out negative numbers. For example, let’s say we have the equation:
3(x-4)
5(4-x)
Notice how (x-4) and (4-x) are ‘’almost’’ identical, but you can’t cross them out because they are reversed. However, (x - 4) can be written as -1 * (4 - x) in the same way that you rewrite (4 + 2x) as 2 * (2 + x). This is called “factoring out the negative.”
-1 * 3(4-x)
5(4-x)
Now we can easily remove the two identical (4-x):
-1 * 3~~(4-x)~~
5~~(4-x)~~
Leaving us with our final answer -3/5
2
Recognize the difference of two squares when working. The difference of two squares is simply one squared number subtracted by another, like the expression (a² - b²). The difference of perfect squares always simplifies into two parts, adding and subtracting the square roots. In every case, you can simplify the difference of perfect square as follows:
a² - b² = (a+b)(a-b) This can be incredibly helpful when trying to find like terms in algebraic fractions.
- Example: x² - 25 = (x+5)(x-5)
3
Simplify any polynomial expressions. Polynomials are complex algebraic expressions with more than two terms, like x² + 4x + 3. Luckily, many polynomials can be simplified using polynomial factorization. The previous expression, for example, can be rewritten as (x+3)(x+1).
4
Remember that variables can be factored out as well. This is especially helpful in expressions with exponents, like x⁴ + x². You can remove the largest exponent as a factor. In this case, x⁴ + x² = x²(x² + 1).

Community Q&A

Question

Why does it work exactly like this all the time?

Donagan

Top Answerer

Because the properties of and operations with numbers never change.
Question

When factoring algebraic fractions, how do I know which one will have a plus or minus sign? For example, 12x^2 + 43x+ 35 / 6x^2 +5x - 21?

Donagan

Top Answerer

This is known as "solving by inspection." In other words, you just look at ("inspect") the expression you're factoring, and choose plus and minus signs so that the factors, when multiplied together, result in the original expression. In the example cited, 12x² + 43x +35 factors into (3x + 7) and (4x + 5). 6x² + 5x - 21 factors into (3x + 7) and (2x - 3). In each case the signs were chosen so that multiplying the factors together would result in the original expression. In this case there is a factor of (3x + 7) in both the numerator and denominator, so that they cancel each other. The final, simplified expression is (4x + 5) / (2x - 3).
Question

What if there's a question like this: (1–y²) / (–y² – y + 2)?

Donagan

Top Answerer

First simplify a little by factoring (-1) from both numerator and denominator: -(y²-1) / -(y²+y-2). The (-1)'s will cancel each other, and you're left with (y²-1) / (y²+y-2). Factor numerator and denominator: [(y+1)(y-1)] / [(y+2)(y-1)]. The two (y-1)'s cancel each other, and the final fraction is (y+1) / (y+2).