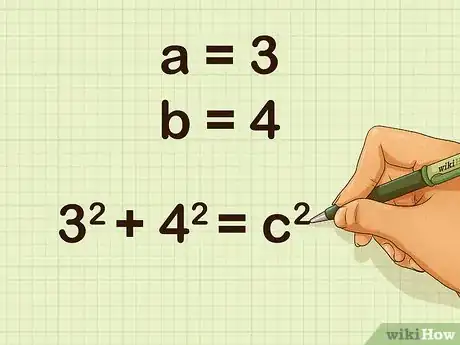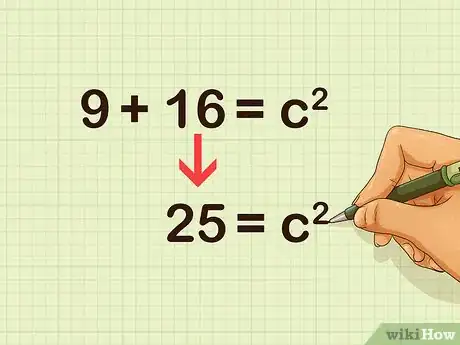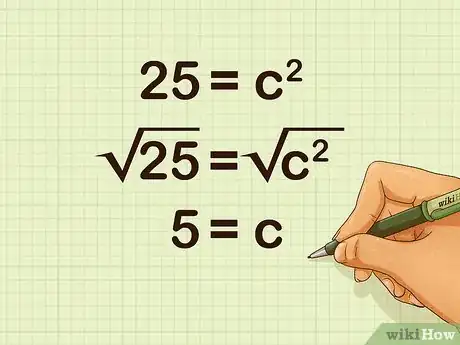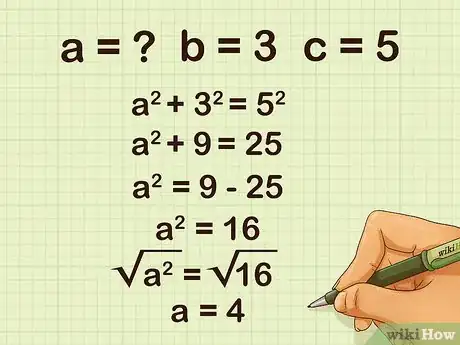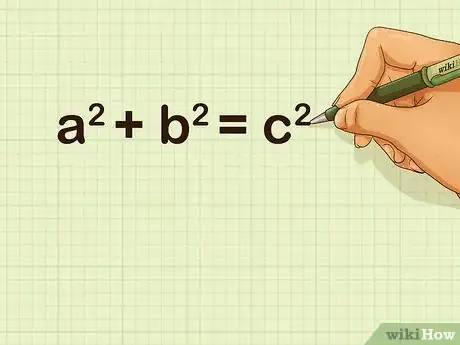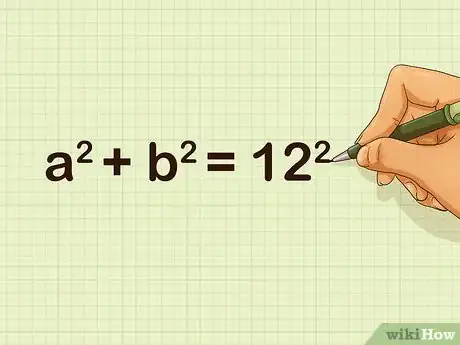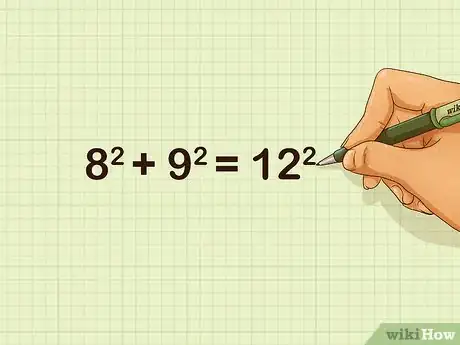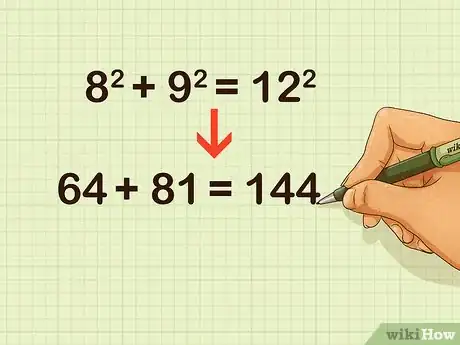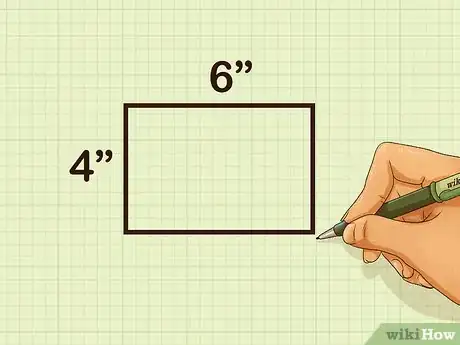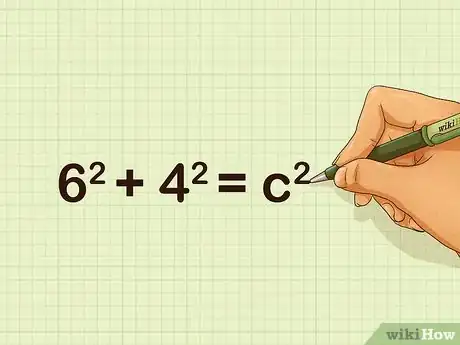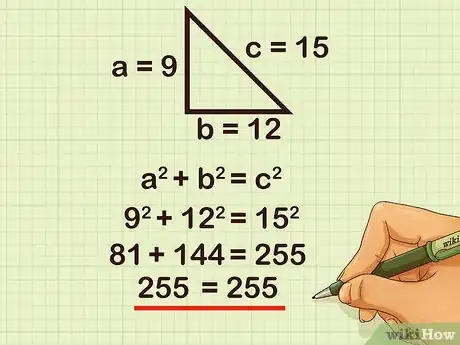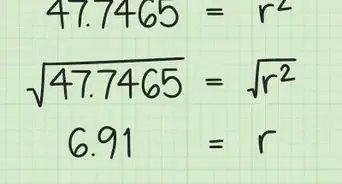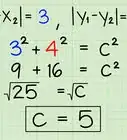This article was co-authored by wikiHow Staff. Our trained team of editors and researchers validate articles for accuracy and comprehensiveness. wikiHow's Content Management Team carefully monitors the work from our editorial staff to ensure that each article is backed by trusted research and meets our high quality standards.
This article has been viewed 39,272 times.
Learn more...
Pythagoras's Theorem is a formula you can use to find an unknown side length of a right triangle. It is one of the most basic geometric tools in mathematics.[1] You will likely come across many problems in school and in real life that require using the theorem to solve. In these problems you might need to directly calculate the side length of a triangle, or use right triangles to calculate measurements of other types of polygons.
Steps
Calculating the Hypotenuse
-
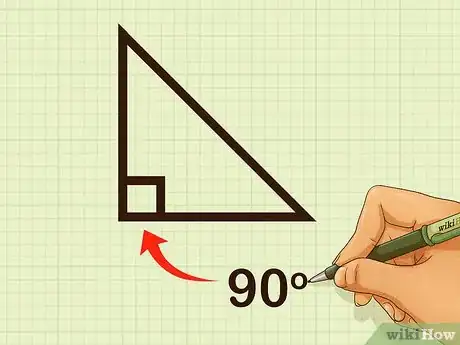
1Find the right, or 90-degree, angle. Because this theorem only applies to right triangles, you need to determine which angle is the right angle. If the triangle does not have a right angle, you cannot use the theorem.
- Usually the right angle is denoted by a small box.
-
2Determine that the missing length is the hypotenuse. The hypotenuse is the longest side of a right triangle, and will be opposite the right angle.[2]Advertisement
-
3Write the formula for Pythagoras's Theorem. The formula is , where is the length of the hypotenuse, and and are the lengths of the other sides of the triangle.[3]
-
4Plug the value of the side lengths into the theorem. Remember, these are represented by the variables and .
- For example, if the triangle has side lengths of 3 and 4 cm, your formula will look like this: .
-
5Square the length of the sides. Plug these new values into the formula.
- For example:
- For example:
-
6Add the squared length of the sides. This sum is equal to the length of the hypotenuse squared ().
- For example:
- For example:
-
7Find the square root of both sides of the equation. This will give you the length of your hypotenuse.
- For example:
So, the length of a hypotenuse of a triangle with side lengths of 3 and 4 cm is 5 cm.
- For example:
-
8Use the theorem to find the sides of triangles. If you know the hypotenuse and one side of the triangle, you can still use the theorem by substituting for the appropriate values.
- For example, if you know a right triangle has a hypotenuse measuring 5 cm in length, and one side measuring 3 cm in length, your formula will look like this: . You would then solve the equation for instead of :
- For example, if you know a right triangle has a hypotenuse measuring 5 cm in length, and one side measuring 3 cm in length, your formula will look like this: . You would then solve the equation for instead of :
Identifying Right Triangles from Three Side Lengths
-
1Ensure that you have the measurements for all three sides of the triangle. If you do not have all three side lengths, you cannot use the Pythagorean Theorem to determine whether the triangle is right.
- For example, you might be given a triangle with side lengths of 8, 9, and 12 cm, and you need to determine whether the triangle is right.
-
2Write the formula for Pythagoras's Theorem. The formula is , where is the length of the hypotenuse, and and are the lengths of the other sides of the triangle.[4]
-
3Plug the length of the potential hypotenuse into the formula. The hypotenuse is the longest side of a right triangle, so whatever measurement is largest will stand for the variable .
- For example, if the side lengths of a triangle are 8, 9, and 12 cm, you would use the measurement of 12 for the potential hypotenuse, because it's the longest side. So, your formula will look like this: .
-
4Plug the values of the other two sides into the equation. It does not matter which value is and which value is .
- For example, if the other two side lengths are 8 and 9 centimeters, your formula will look like this: .
-
5Square all of the numbers. Remember that squaring a number means to multiply it by itself.
- For example:
- For example:
-
6Add the square of the two sides. If this sum is equal to the square of the hypotenuse, the triangle is right. If the two sides of the equation are not equal, the triangle is not right.[5]
- For example:
Since the equation is not true, the triangle is not right.
- For example:
Finding the Diagonal of a Rectangle
-
1Ensure the polygon is a rectangle. A rectangle is a four-sided shape with four 90-degree angles.[6]
-
2Make sure you have the length and width of the rectangle. If you do not have these measurements, you cannot use this method.
- For example, you might be asked to use the Pythagorean Theorem to find the length of the diagonal of a 6-inch by 4-inch rectangle.
-
3Locate or draw the diagonal of the rectangle. Since the diagonal of a rectangle divides the shape into two congruent right triangles, you can use Pythagoras's Theorem to find its length.
- The length of the diagonal will equal the length of the hypotenuse of the right triangles.
-
4Set up the formula for Pythagoras's Theorem. The formula is , where is the length of the hypotenuse, and and are the lengths of the other sides of the triangle.[7]
-
5Plug the values of the rectangle's length and width into the formula. Make sure you substitute for the variables and . It doesn't matter which variable is the length and which is the width.
- For example, for a 6-inch by 4-inch rectangle, the formula will look like this: .
-
6Square the length and width. Remember that squaring means to multiply a number by itself.
- For example:
- For example:
-
7Add the squared side lengths. This sum will give you the value of the hypotenuse, or diagonal, squared.
- For example:
- For example:
-
8Find the square root of both sides. This will give you the value of , which is the length of the right triangle's hypotenuse, and also the length of the rectangle's diagonal.
- For example:
So, the diagonal of a 6-inch by 4-inch rectangle is 7.21 inches.
- For example:
Solving Sample Test Questions
-
1Find the shortest distance between two points. For instance, Luis walks through a park. He starts at the fountain and walks 80 feet south and 60 feet west. What is the shortest distance back to the fountain?
- The shortest distance between two points is a straight line. This straight line creates a hypotenuse of a right triangle, with one side 80 feet long and the other side 60 feet long.
- The formula for Pythagoras's theorem is , where equals the length of the hypotenuse, and and equal the lengths of the other two sides.
- Since you know the lengths of the two sides, plug the values of and into the formula: .
- Square the lengths of the sides: .
- Add the squared side lengths: .
- Find the square root of both sides of the equation:
. - The length of hypotenuse, and the shortest distance back to the fountain, is 100 ft.
-
2Find a missing length. For instance, find the length of , given a right triangle with a hypotenuse measuring 10 cm and one side measuring 6 cm.
- The formula for Pythagoras's theorem is , where equals the length of the hypotenuse, and and equal the lengths of the other two sides.
- Since you know the lengths of the hypotenuse and one side, plug the values of and into the formula: .
- Square the known measurements: .
- Subtract the squared value of from both sides of the equation: .
- Find the square root of both sides of the equation:
- The length of is 8 cm.
-
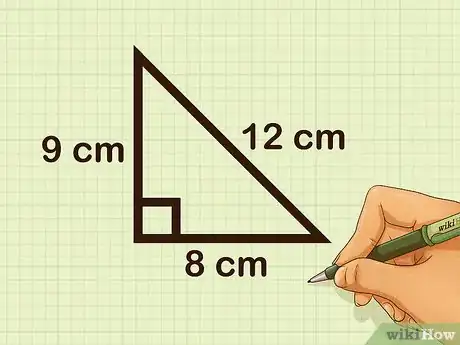
3Identify a right triangle. For instance, determine whether the triangle is right, given side lengths of 9, 12, and 15 cm.
- The formula for Pythagoras's theorem is , where equals the length of the hypotenuse, and and equal the lengths of the other two sides.
- The longest side length is the potential hypotenuse. Plug this value in for : .
- Plug the values of the other two sides into the equation: .
- Square all of the numbers: .
- Add the square of the two sides: .
- Since the equation is true, the triangle is right.
-
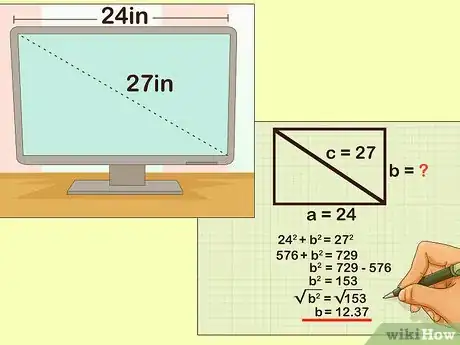
4Use the diagonal of a rectangle as the hypotenuse of a right triangle. For instance, Sherrie is buying a new computer screen. It needs to be less than 12 inches high to be able to fit under the shelf over her desk. She finds a computer screen with a 27-inch diagonal, and a width of 24 inches. Will this screen fit on her desk?
- The formula for Pythagoras's theorem is , where equals the length of the hypotenuse, and and equal the lengths of the other two sides.
- Since you know the width and the diagonal of the rectangle, plug the values of and into the formula: .
- Square the known measurements: .
- Subtract the squared value of from both sides of the equation: .
- Find the square root of both sides of the equation:
- The height of the computer screen is about 12.37 inches. Sherrie only has room for a screen that is 12 inches high, so this screen will not fit on her desk.
Community Q&A
-
QuestionHow do I prove that angle A is equal to angle B?
 DonaganTop AnswererThere are many ways to prove two angles equal. Among them are: show that corresponding sides of the angles are parallel to each other; show that they are opposite angles in a rectangle, parallelogram, isosceles triangle or isosceles trapezoid; show that they are formed by two perpendicular lines; or show that they are corresponding angles of congruent or similar triangles. There are also several other ways to prove angles equal.
DonaganTop AnswererThere are many ways to prove two angles equal. Among them are: show that corresponding sides of the angles are parallel to each other; show that they are opposite angles in a rectangle, parallelogram, isosceles triangle or isosceles trapezoid; show that they are formed by two perpendicular lines; or show that they are corresponding angles of congruent or similar triangles. There are also several other ways to prove angles equal. -
QuestionWhat if I only know one side?
 Community AnswerTo use the Pythagorian Theorem you MUST know two sides. This may mean you have to use trigonometry to find another side. If you are still confused, ask your teacher.
Community AnswerTo use the Pythagorian Theorem you MUST know two sides. This may mean you have to use trigonometry to find another side. If you are still confused, ask your teacher.
References
- ↑ http://mathworld.wolfram.com/PythagoreanTheorem.html
- ↑ http://mathworld.wolfram.com/Hypotenuse.html
- ↑ https://www.mathsisfun.com/pythagoras.html
- ↑ https://www.mathsisfun.com/pythagoras.html
- ↑ http://www.purplemath.com/modules/pythagthm.htm
- ↑ http://www.mathopenref.com/rectangle.html
- ↑ https://www.mathsisfun.com/pythagoras.html