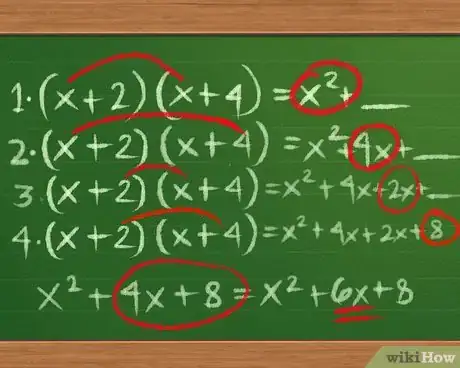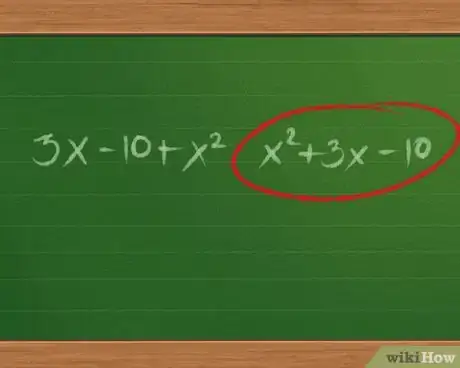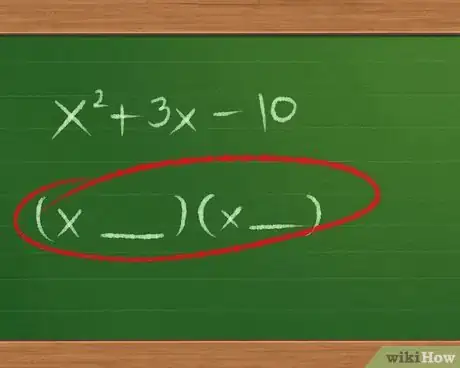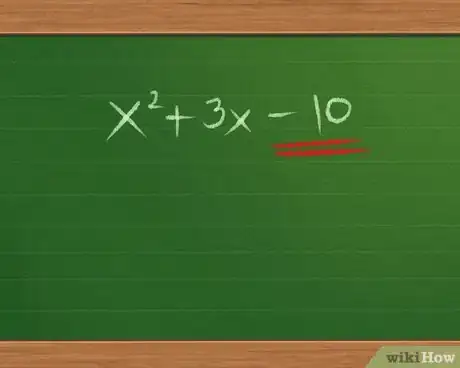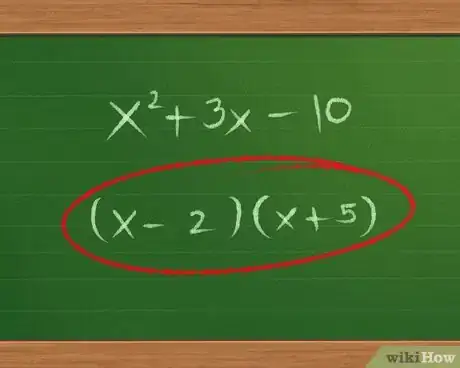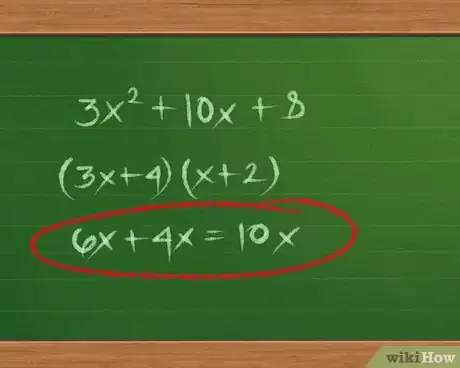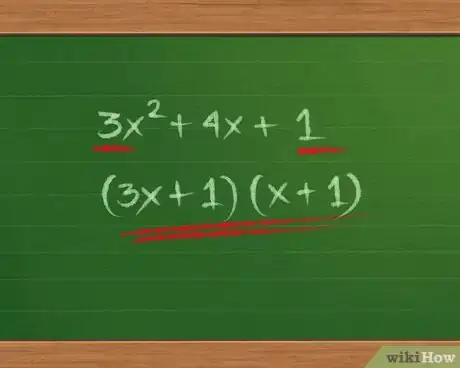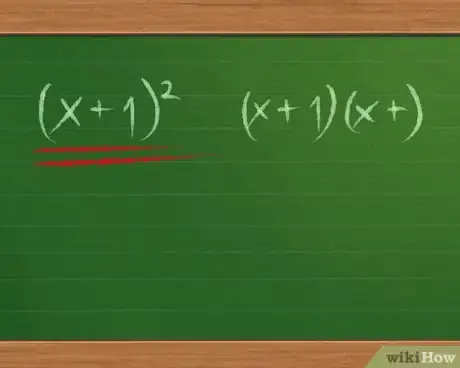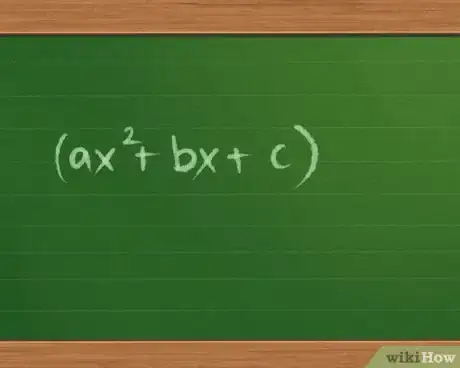wikiHow es un "wiki", lo que significa que muchos de nuestros artículos están escritos por varios autores. Para crear este artículo, 26 personas, algunas anónimas, han trabajado para editarlo y mejorarlo con el tiempo.
Este artículo ha sido visto 861 427 veces.
Un trinomio es una expresión algebraica compuesta por tres términos. Lo más probable es que primero aprendas a factorizar trinomios "cuadráticos"; es decir, los trinomios escritos de la forma ax2 + bx + c. Hay varios trucos que puedes aprender y que aplican a diferentes tipos de trinomios cuadráticos, los cuales aprenderás a usar mejor y más rápido con un poco de práctica. Los polinomios de mayor grado, con términos como x3 o x4, no siempre se pueden resolver utilizando los mismos métodos, pero por lo general puedes utilizar una factorización simple o el método por sustitución para convertirlos en problemas que puedan resolverse como cualquier fórmula cuadrática.
Pasos
Método 1
Método 1 de 3:Factorizar trinomios de la forma x2 + bx + c
-
1Aprende el método de multiplicación FOIL. Tal vez ya conozcas el método FOIL (por sus siglas en inglés), el cual significa "primero, exterior, interior y último", y se usa para multiplicar expresiones como (x+2)(x+4). Es de gran ayuda saber cómo funciona dicho método antes de factorizar. Este se realiza de la siguiente manera:
- Multiplica los primeros términos: (x+2)(x+4) = x2 + __
- Multiplica los términos exteriores: (x+2)(x+4) = x2+4x + __
- Multiplica los términos interiores: (x+2)(x+4) = x2+4x+2x + __
- Multiplica los últimos términos: (x+2)(x+4) = x2+4x+2x+8
- Simplifica: x2+4x+2x+8 = x2+6x+8
-
2Comprende el proceso de factorización. Cuando multiplicas dos binomios utilizando el método FOIL, el resultado es un trinomio (una expresión con tres términos) de la forma ax2+bx+c, donde a, b y c son números normales. Si te dan una ecuación con esa misma forma, puedes factorizarla para convertirla en dos binomios.
- Si la ecuación no se encuentra escrita de esa forma, reorganiza los términos. Por ejemplo, reescribe3x - 10 + x2 como x2 + 3x - 10.
- Debido a que el mayor exponente es 2 (x2), este tipo de expresión se denomina "cuadrática".
-
3Deja un espacio para la respuesta. Por el momento, solo debes escribir (__ __)(__ __), en el espacio donde planees escribir tu respuesta. Vas a llenar los campos a medida que avances.
- Todavía no escribas + o - en medio de los términos en blanco, ya que desconocemos el signo.
-
4Completa los primeros términos. Para problemas sencillos, donde el primer término del trinomio es x2, los términos en las primeras líneas siempre serán x y x. Esos son los factores del término x2, ya que x por x = x2.
- Nuestro ejemplo x2 + 3x - 10 empieza con x2, por lo que podemos escribir lo siguiente:
- (x __)(x __)
- Cubriremos problemas más complicados en la próxima sección, incluyendo trinomios que empiecen con un término como 6x2 o -x2. Por ahora, sigue el ejemplo.
-
5Utiliza la factorización para hallar los últimos términos. Si regresas y revisas el método FOIL, te darás cuenta de que al multiplicar los últimos términos obtendrás el término final del polinomio (el que no tiene x). Por ello, para factorizar, necesitarás encontrar dos números que multiplicados den el último término.
- En nuestro ejemplo, x2 + 3x - 10, el último término es -10.
- ¿Cuáles son los factores de -10? ¿Qué números multiplicados dan como resultado -10?
- Hay varias posibilidades: -1 x 10, 1 x -10, -2 x 5 y por último 2 x -5. Escribe estos conjuntos de números para que no los olvides.
- Aún no escribas la respuesta. Todavía debe verse así: (x __)(x __).
-
6Define la respuesta correcta multiplicando el número interior por el exterior. Hemos disminuido la búsqueda de los últimos términos a solo un par de posibilidades. Utiliza el ensayo y error para probar cada posibilidad, multiplicando el término exterior por el interior y comparando el resultado con el trinomio. Por ejemplo:
- El problema original tiene un término "x" de 3x, por lo que debemos conseguir ese término con la multiplicación.
- Probemos con -1 y 10: (x-1)(x+10). El exterior + el interior = 10x - x = 9x. No es la respuesta.
- Probemos con 1 y -10: (x+1)(x-10). -10x + x = -9x. Tampoco es la respuesta. De hecho, ya que probamos con -1 y 10, sabemos que si utilizamos 1 y -10, obtendremos la misma respuesta con el signo contrario: -9x en lugar de 9x.
- Probemos con -2 y 5: (x-2)(x+5). 5x - 2x = 3x. Esta respuesta coincide con el polinomio original, por lo que es la respuesta correcta: (x-2)(x+5).
- En casos sencillos como el anterior, cuando no hay una constante al lado del término x2, puedes utilizar un atajo: simplemente suma los dos factores y añade una "x" (-2+5 → 3x). Pero este truco no funciona para problemas más complicados, por lo que es bueno recordar la "forma larga" descrita anteriormente.
Método 2
Método 2 de 3:Factorizar trinomios más complicados
-
1Utiliza la factorización simple para facilitar los problemas más complicados. Supongamos que vamos a factorizar 3x2 + 9x - 30. Busca el factor de los tres términos (el "máximo factor común" o MFC).[1] En este caso, es 3:
- 3x2 = (3)(x2)
- 9x = (3)(3x)
- -30 = (3)(-10)
- Por lo tanto, 3x2 + 9x - 30 = (3)(x2+3x-10). Podemos factorizar el nuevo trinomio utilizando los pasos descritos en la sección anterior. La respuesta final será (3)(x-2)(x+5).
-
2Halla factores más complicados. En ocasiones, el factor puede ir acompañado de una variable o tal vez debas factorizar varias veces para hallar la expresión más simple posible. Aquí tienes algunos ejemplos:
- 2x2y + 14xy + 24y = (2y)(x2 + 7x + 12)
- x4 + 11x3 - 26x2 = (x2)(x2 + 11x - 26)
- -x2 + 6x - 9 = (-1)(x2 - 6x + 9)
- No te olvides de factorizar cada nuevo trinomio que obtengas, utilizando los pasos descritos en el método 1. Comprueba tus resultados y busca ejemplos similares en la sección de problemas en la parte inferior de esta página.
-
3Resuelve los trinomios que tengan un número que acompañe el término x2. Algunos trinomios cuadráticos no se pueden simplificar para resolverlos de forma sencilla. Aprende a resolver problemas similares a 3x2 + 10x + 8 y luego práctica por tu cuenta con los problemas en la parte inferior de la página:
- Dejemos espacio para la respuesta: (__ __)(__ __)
- Los "primeros" términos deben tener una x y tenemos que multiplicarlos para obtener 3x2. Solo existe una única solución: (3x __)(x __).
- Escribe los factores de 8. Nuestras opciones son 1 x 8 o 2 x 4.
- Prueba multiplicando el término exterior con el término interior. Ten en cuenta el orden de los factores, ya que debes multiplicar el término exterior por 3x en lugar de x. Prueba todas las opciones hasta obtener como resultado 10x (el término del problema original):
- (3x+1)(x+8) → 24x+x = 25x no
- (3x+8)(x+1) → 3x+8x = 11x no
- (3x+2)(x+4) → 12x+2x=14x no
- (3x+4)(x+2) → 6x+4x=10x sí. Este es el factor correcto.
-
4Utiliza el método por sustitución para los trinomios de mayor grado. Tal vez te den una ecuación con un exponente mayor a dos (como por ejemplo x4) incluso después de haber factorizado para simplificar el problema. Sustituye con una variable que convierta el problema en uno que sepas cómo resolver.[2] Por ejemplo:
- x5+13x3+36x
- =(x)(x4+13x2+36)
- Creemos una nueva variable. Supongamos y = x2 y reemplacemos:
- (x)(y2+13y+36)
- =(x)(y+9)(y+4). Ahora reemplacemos con la variable original:
- =(x)(x2+9)(x2+4)
- =(x)(x±3)(x±2)
Método 3
Método 3 de 3:Factorizar casos especiales
-
1Busca números primos. Comprueba que la constante en el primer o tercer término del trinomio sea un número primo. Un número primo se puede dividir para obtener un número exacto solo por sí mismo y uno, por lo que solo hay un posible par de factores para introducir en el binomio.
- Por ejemplo, en x2 + 6x + 5, 5 es un número primo, por lo que el binomio debe tener la forma (__ 5)(__ 1).
- En el problema 3x2+10x+8, 3 es un número primo, por lo que el binomio debe tener la forma (3x __)(x __).
- Para el problema 3x2+4x+1, el 3 y el 1 son números primos, por lo que la única solución posible es (3x+1)(x+1). (De todas formas debes resolver la multiplicación para comprobar, ya que algunas expresiones no se pueden factorizar, por ejemplo, la ecuación 3x2+100x+1, no tiene factores).
-
2Revisa si el trinomio es un cuadrado perfecto. Un trinomio cuadrado perfecto se puede factorizar en dos binomios idénticos y el factor resultante normalmente se escribe como (x+1)2 en lugar de (x+1)(x+1). Aquí tienes algunos ejemplos que suelen verse en los problemas de álgebra:
- x2+2x+1=(x+1)2 y x2-2x+1=(x-1)2
- x2+4x+4=(x+2)2 y x2-4x+4=(x-2)2
- x2+6x+9=(x+3)2 y x2-6x+9=(x-3)2
- Un trinomio cuadrado perfecto de la forma ax2 + bx + c siempre tiene términos de a y c que son cuadrados perfectos positivos (como 1, 4, 9, 15 o 25) y el término b (positivo o negativo) es igual a 2(√a * √c).[3]
-
3Comprueba que el problema tenga solución. No todos los trinomios pueden factorizarse. Si no puedes resolver un trinomio cuadrático (ax2+bx+c), utiliza la fórmula cuadrática para hallar la respuesta. Si las únicas soluciones son la raíz cuadrada de un número negativo (es decir, no existe solución real), entonces el trinomio no puede factorizarse.
- Para trinomios no cuadráticos, utiliza el criterio de Eisenstein, descrito en la sección de consejos.
Problemas y soluciones
-
Respuestas a problemas de factorización "complicados". Estos son los problemas del paso sobre "factores más complicados". Ya han sido simplificados a trinomios sencillos, así que intenta resolverlos utilizando los pasos descritos en el método 1, luego comprueba tus respuestas aquí:
- (2y)(x2 + 7x + 12) = (x+3)(x+4)
- (x2)(x2 + 11x - 26) = (x+13)(x-2)
- (-1)(x2 - 6x + 9) = (x-3)(x-3) = (x-3)2
-
Intenta con problemas de factorización más complicados. Estos problemas tienen un factor común en cada término que primero debe factorizarse. Sombrea el espacio luego del signo de igual para ver la respuesta y comprobar tu trabajo:
- 3x3+3x2-6x = (3x)(x+2)(x-1) ← sombrea este espacio para ver la respuesta.
- -5x3y2+30x2y2-25y2x = (-5xy^2)(x-5)(x-1)
-
Práctica con problemas difíciles. Los siguientes problemas no pueden factorizarse en soluciones sencillas, por lo que debes hallar la respuesta de la forma (_x + __)(_x + __) por medio de ensayo y error:
- 2x2+3x-5 = (2x+5)(x-1) ← sombrea para ver la respuesta.
- 9x2+6x+1 = (3x+1)(3x+1)=(3x+1)2 (Pista: tal vez debas probar con más de un par de factores para el término 9x).
Consejos
- Si no puedes factorizar un trinomio cuadrático (ax2+bx+c), puedes utilizar la fórmula cuadrática para hallar el valor de x.
- Aunque no es necesario saberlo, puedes utilizar el criterio de Eisenstein para determinar rápidamente si el polinomio es irreducible, en cuyo caso no puede factorizarse. Este criterio funciona para cualquier tipo de polinomio, pero funciona mejor en los trinomios. Si hay un número primo (p) que divida de forma exacta los dos últimos términos y cumpla las siguientes condiciones, entonces el polinomio es irreducible:
- El término constante (el que no tiene variable) es un múltiplo de p, pero no de p2.
- El primer término (por ejemplo, a en ax2+bx+c) no es un múltiplo de p.
- Por ejemplo, 14x2 + 45x + 51, es irreducible porque hay un número primo (3) que divide de forma exacta a 45 y 51, pero no a 14; y 51 no se puede dividir de forma exacta entre 32.
Advertencias
- Aunque es cierto para los trinomios cuadráticos, los trinomios factorizables no son necesariamente el producto de dos binomios. Por ejemplo, x4 + 105x + 46 = (x2 + 5x + 2)(x2 - 5x + 23).
Referencias
- ↑ http://www.wtamu.edu/academic/anns/mps/math/mathlab/int_algebra/int_alg_tut28_facttri.htm
- ↑ http://www.regentsprep.org/regents/math/algtrig/ate13/highpolylesson.htm
- ↑ http://www.themathpage.com/alg/perfect-square-trinomial.htm
- http://www.wtamu.edu/academic/anns/mps/math/mathlab/int_algebra/int_alg_tut28_facttri.htm
- http://www.themathpage.com/alg/factoring-trinomials.htm
- http://www.algebrahelp.com/lessons/factoring/trinomial/