wikiHow es un "wiki", lo que significa que muchos de nuestros artículos están escritos por varios autores. Para crear este artículo, 45 personas, algunas anónimas, han trabajado para editarlo y mejorarlo con el tiempo.
Este artículo ha sido visto 48 734 veces.
Los factores de un números son aquellos que al multiplicarse dan como resultado dicho número. Otra forma de pensar en esto es que cada número es el producto de factores múltiples. Aprender cómo factorizar ; es decir, descomponer un número en sus factores componentes, es una habilidad matemática importante que se usa no solo en la aritmética básica sino también en álgebra, cálculo y demás. ¡Revisa el paso 1 para empezar a aprender a factorizar!
Pasos
Método 1
Método 1 de 2:Factorizando números enteros básicos
-
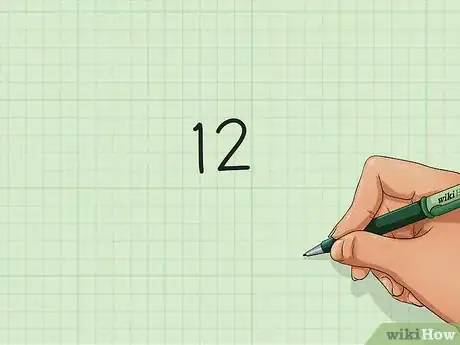
1Escribe tu número. Para empezar a factorizar, todo lo que necesitas es un número, cualquier número funcionará, pero para nuestros propósitos, empecemos con un número entero simple. Los números enteros son aquellos números que no tienen un componente fraccional o decimal (todos los números positivos y negativos son números enteros).
- Elijamos el número 12. Anota este número en un papel.
-
2Halla otros dos números que multiplicados den tu primer número. Cualquier número entero puede ser el producto de otros dos números enteros. Incluso los números primos pueden ser el producto de 1 y el mismo número. Pensar en un número que pueda ser el producto de dos factores necesitará pensar "hacia atrás", básicamente tienes que preguntarte : "¿qué operación de multiplicación da como resultado este número?"
- En el ejemplo, 12 tienes varios factores : 12 × 1, 6 × 2, y 3 × 4 todos dan como resultado 12. Así que podemos decir que los factores de 12 son 1, 2, 3, 4, 6, y 12. Para este efecto, se trabajará con los factores 6 y 2.
- Es más fácil factorizar los números pares, pues todos los números pares tienen al número 2 como factor. 4 = 2 × 2, 26 = 13 × 2, etc.
-
3Determina si alguno de tus factores se puede factorizar otra vez. Muchos números, especialmente los más altos, se pueden factorizar varias veces. Cuando halles dos de los factores de un número, si uno de ellos tiene sus propios factores, también puedes reducir este número a sus factores. De acuerdo a la situación, puede ser o no beneficioso hacer esto.
- Por ejemplo, en el caso se redujo 12 a 2 × 6. Observa que 6 tiene sus propios factores: 3 × 2 = 6. Es por eso que se puede afirmar que 12 = 2 × (3 × 2).
-
4Deja de factorizar cuando llegues a los números primos. Los números primos son aquellos números que solo se pueden dividir entre 1 o sí mismos. Por ejemplo, 1, 2, 3, 5, 7, 11, 13, y 17 son números primos. Cuando hayas factorizado un número en números primos, seguir factorizando es irrelevante. No te beneficia seguir reduciendo cada factor en sí mismo o en uno, así que puedes detenerte.
- En el ejemplo, se redujo 12 a 2 × (2 × 3). 2, 2, y 3 son números primos. Si seguimos factorizando, tendríamos (2 × 1) × ((2 × 1)(3 × 1)) lo cual es inútil y por eso frecuentemente se evita.
-
5Factoriza los números negativos de la misma forma. Los números negativos se pueden factorizar casi de la misma forma que los números positivos. La única diferencia es que al mutiplicar los números negativos debe resultar un número negativo como producto, así que una cantidad impar de los factores debe ser negativa.
- Por ejemplo, factorizar -60. Ver abajo:
- -60 = -10 × 6
- -60 = (-5 × 2) × 6
- -60 = (-5 × 2) × (3 × 2)
- -60 = -5 × 2 × 3 × 2. Observa que tener una cantidad impar de números negativos aparte de uno dará como resultado el mismo producto. Por ejemplo, -5 × 2 × -3 × -2 también da 60.
Anuncio - Por ejemplo, factorizar -60. Ver abajo:
Método 2
Método 2 de 2:Estrategia para factorizar números altos
-
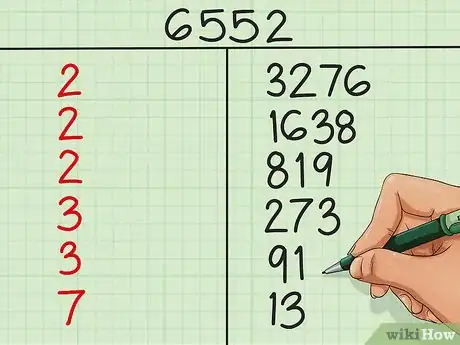
1Escribe tu número sobre una tabla de 2 columnas. Mientras que por lo general es mucho más fácil factorizar números enteros pequeños, hacerlo con números más altos puede ser más desafiante. Para muchos sería más difícil descomponer un número de 4 o 5 dígitos en sus factores primos usando solamente las matemáticas mentales. Por suerte, si se usa una tabla, el proceso se hace más fácil. Escribe tu número sobre un tabla en forma de "t" que tenga dos columnas; usarás esta tabla para controlar la creciente lista de factores.
- Para los efectos de este ejemplo, se elige un número de 4 dígitos para factorizar: 6552.
-
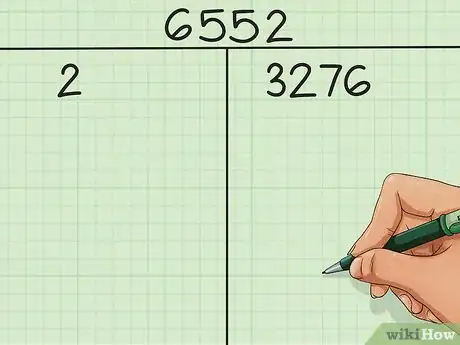
2Divide tu número entre el factor primo más pequeño posible. Divide el número entre el factor primo más pequeño (aparte de 1) que lo divida exactamente (sin residuo). Escribe el factor primo en la columna de la izquierda y la respuesta en la columna derecha. Como ya se mencionó, los números pares son más fáciles de factorizar pues su factor primo más pequeño siempre será 2. Por otro lado, los números impares tendrán un factor primo diferente.
- En el ejemplo, ya que 6552 es par, se sabe que 2 es su factor primo más pequeño. 6552 ÷ 2 = 3276. En la columna de la izquierda se escribe 2, y en la columna derecha 3276.
-
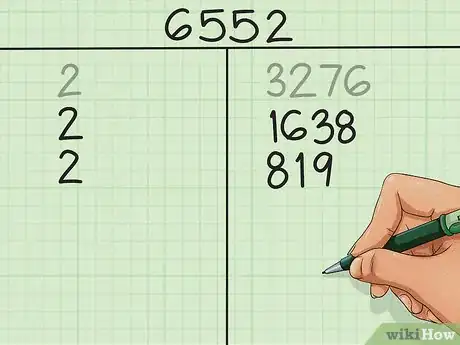
3Sigue factorizando de esta manera. A continuación, factoriza el número que está en la columna de la derecha entre su factor primo más pequeño, en lugar del número que están en la parte superior de la tabla. Escribe el factor primo en la columna de la izquierda y el nuevo número en la columna de la derecha. Continúa repitiendo este proceso; con cada repetición el número de la derecha será cada vez más pequeño.
- Continúa con ese proceso. 3276 ÷ 2 = 1638, así que al final de la columna de la izquierda se escribe otro 2 y 819 al final de las dos columnas.
-
4Trabaja con los impares al intentar con los factores primos. Es más difícil encontrar los factores primos de los impares que de los pares, porque no tienen al número 2 como su factor primo más pequeño. Cuando tengas un número impar, intenta dividir entre números primos pequeños diferentes al número 2; pueden ser 3,5,7, 11, y así sucesivamente, hasta que encuentres un número que lo divida de forma exacta. Este será el factor primo más pequeño del número.
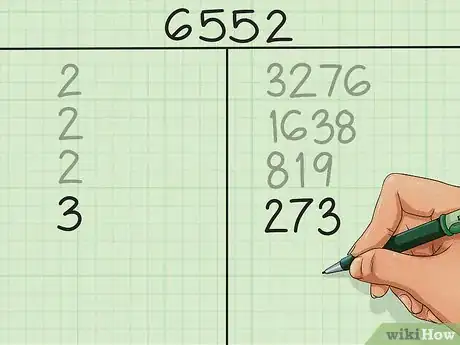
- En el ejemplo, tenemos 819. El número 819 es impar, así que 2 no es un factor de 819. En lugar de escribir el número 2, se intenta con el siguiente número primo: 3. 819 ÷ 3 = 273, sin residuo, así que se escribe 3 y 273.
- Cuando se adivinen los factores, debes intentar con todos los números primos hasta la raíz cuadrada del factor más alto que has hallado hasta entonces. Si ninguno de los factores con los que intentaste lo dividen de forma exacta, es probable que sea un número primo y de este modo, se termina con el proceso de factorización.
-
5Continúa hasta que llegues al número 1. Sigue dividiendo los números de la columna de la derecha entre el factor primo más pequeño hasta que obtengas un número primo en la columna de la derecha. Divide el número entre sí mismo; de esta forma el número estará en la columna de la izquierda y 1 en la columna de la derecha.
- Termina de factorizar tu número. A continuación encontrarás una descomposición detallada:
- Divide entre 3 nuevamente: 273 ÷ 3 = 91, sin residuo, así que escribe 3 y 91.
- Intenta nuevamente con 3: 91 no tiene como factor al 3 ni al 5, que es el siguiente número primo más pequeño, pero 91 ÷ 7 = 13, sin residuo, así que se escribe 7 y 13.
- Intenta nuevamente con 7: 13 no tiene como facto al 7, ni al 11 (el siguiente número primo), pero se tiene a sí mismo como factor: 13 ÷ 13 = 1. Así que para terminar la tabla, escribe 13 y 1. Finalmente podemos dejar de factorizar.
- Termina de factorizar tu número. A continuación encontrarás una descomposición detallada:
-
6Usa los números que están en la columna de la izquierda como los factores originales del número. Una vez que hayas llegado al 1 en la columna de la derecha, ya habrás terminado. Los números que están en el lado izquierdo de la tabla son tus factores. En otras palabras, cuando multipliques todos estos números el producto será el número que aparece en la parte superior de la tabla. Si el mismo factor aparece varias veces, puedes utilizar la notación del exponente par ahorrar espacio. Por ejemplo, si tu lista de factores tiene cuatro veces el número 2, puedes escribir 24 en lugar de 2 × 2 × 2 × 2.
- En el ejemplo 6552=23 × 32 × 7 × 13. Esta es la factorización completa de 6552 en sus números primos. Sin importar el orden en el que se multipliquen los números el producto será 6552.
Anuncio
Consejos
- Asimismo, es importante el concepto de número primo: un número que solo tiene dos factores, 1 y el mismo número. El número 3 es primo porque sus únicos factores son 3 y 1. Por otro lado, el número 4 tiene al 2 como factor. Un número que no es primo se llama compuesto. (No obstante, el número 1 en sí, no se considera ni primo ni compuesto; es un caso en especial).
- Los números primos más bajos son 2, 3, 5, 7, 11, 13, 17, 19, y 23.
- Comprende que un número es el factor del otro número más alto si la división es "exacta"; es decir, el número más alto se puede dividir entre un número más bajo sin dejar residuo. Por ejemplo, 6 es un factor de 24, porque 24 ÷ 6 = 4, sin residuo. Por otro lado, 6 no es un factor de 25.
- Recuerda que solo se habla de "números naturales", a los que a veces también se llama "números cardinales": 1, 2, 3, 4, 5... No se hace referencia a los números negativos o a las fracciones que pueden merecer su propio artículo.
- Algunos números se pueden factorizar de forma más rápida, pero este método siempre funciona y, como ventaja, al terminar tendrás a los factores primos ordenados de forma ascendente.
- Si sumas los dígitos de un número y el resultado es un múltiplo de 3, entonces el primer número también es un múltiplo de 3. (819= 8+1+9 que es =18, 1+8=9. Tres es un factor de nueve así que también es un factor de 819).
Advertencias
- No realices trabajo en vano. Cuando hayas eliminado un potencial factor, no tienes que probarlo nuevamente. Se se prueba que 2 no es un factor de 819, no se debe probar el número 2 en lo que queda del proceso.
Cosas que necesitarás
- Papel
- Útiles para escribir, preferentemente lápiz y borrador
- Calculadora (opcional)




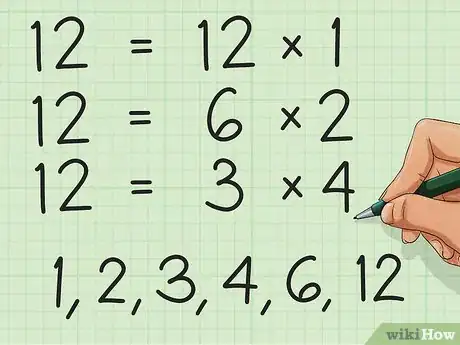
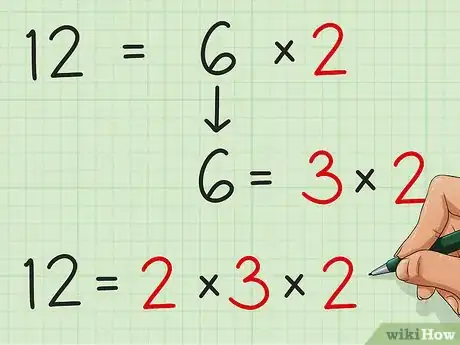

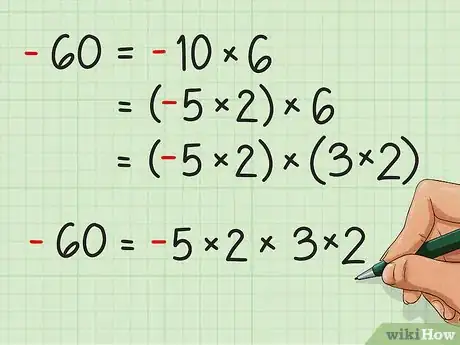

-Step-31-Version-2.webp)









-Step-31-Version-2.webp)



