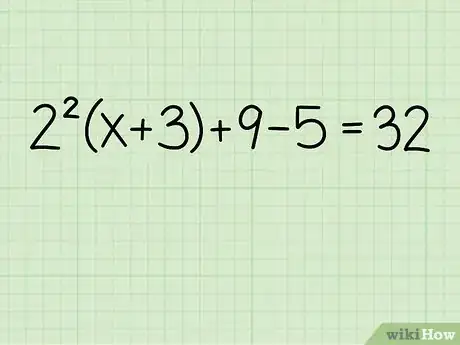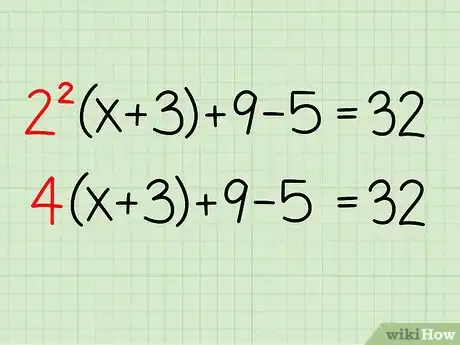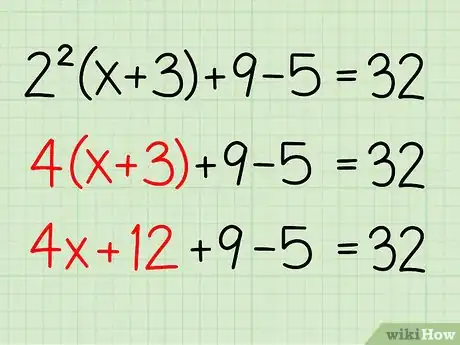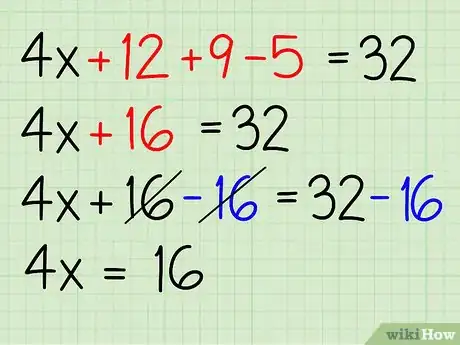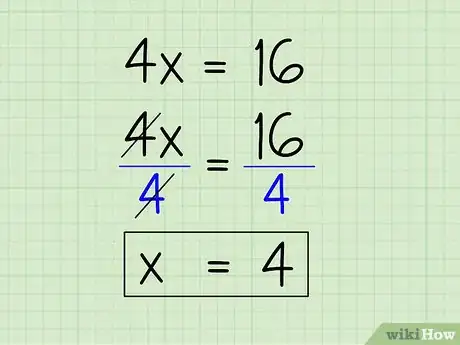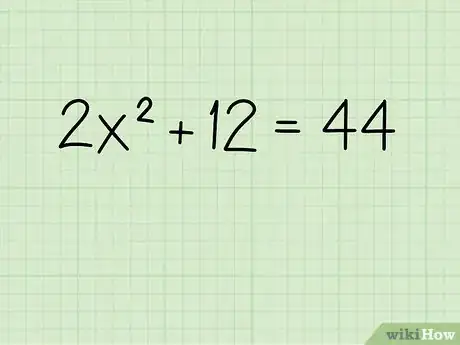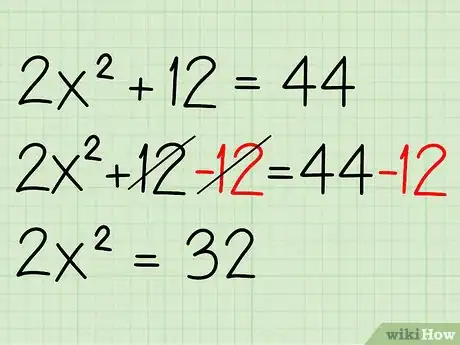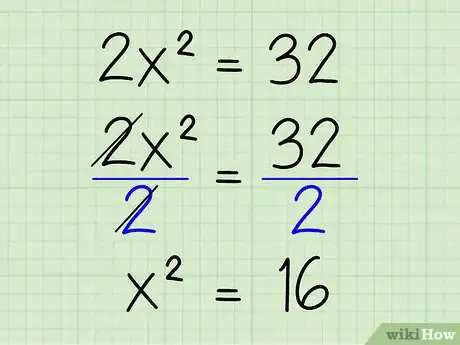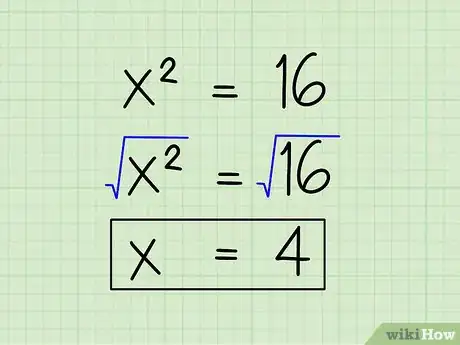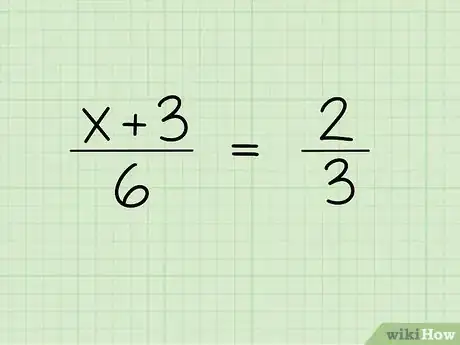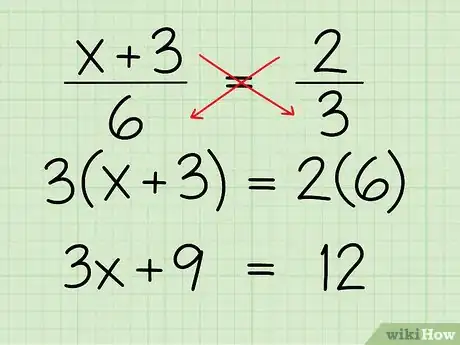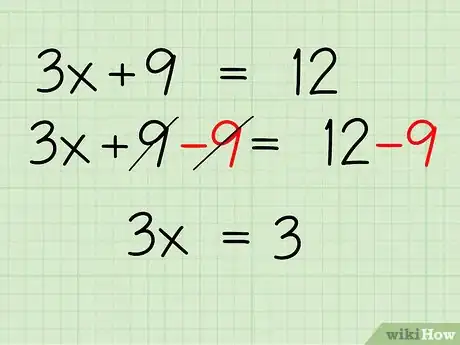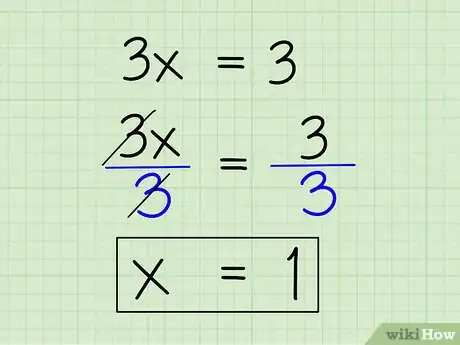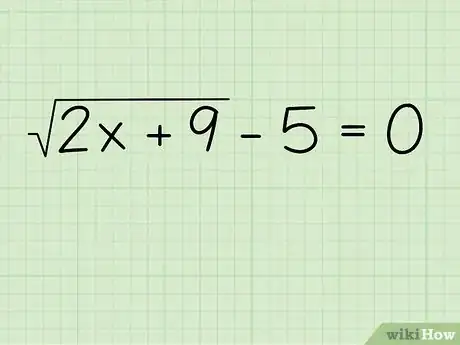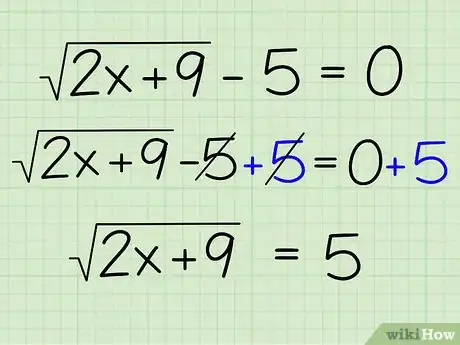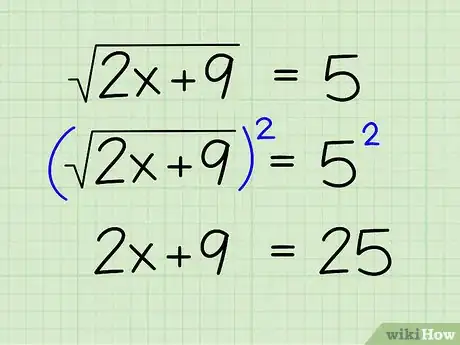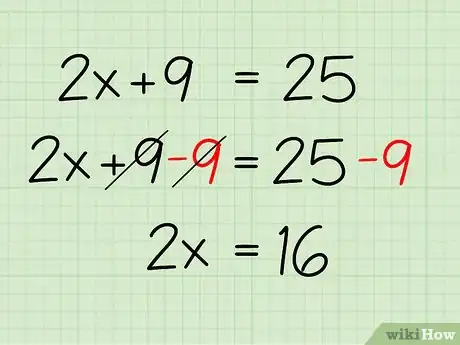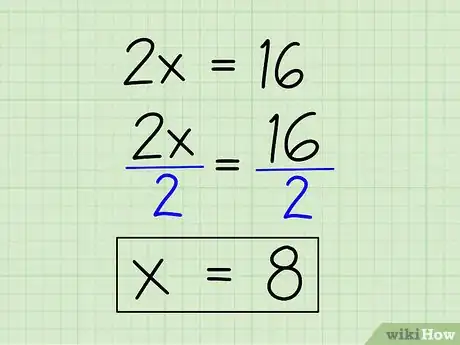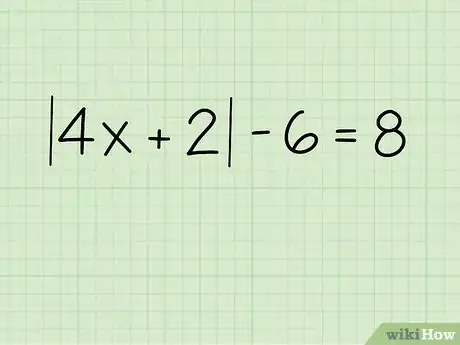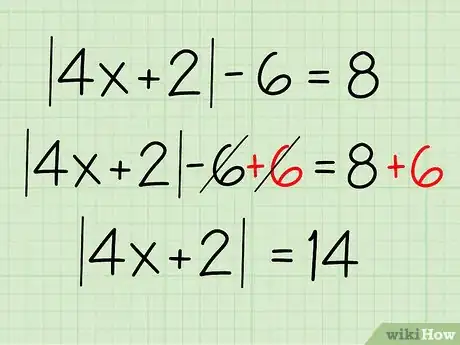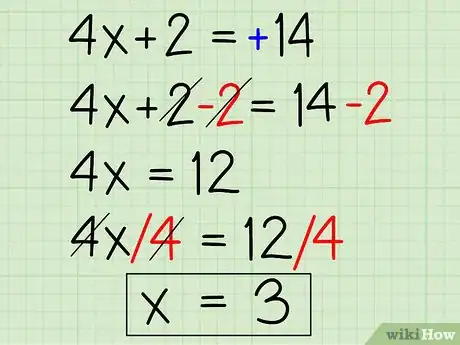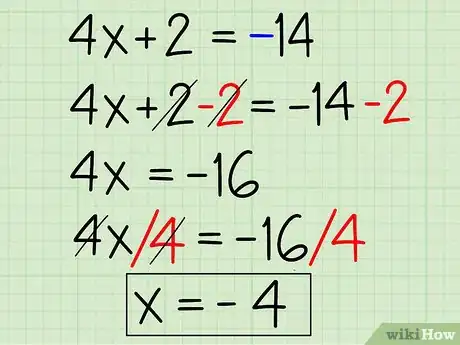Cómo encontrar el valor de X

Coescrito por David Jia

Hay varias maneras de calcular x, ya sea que trabajes con exponentes y radicales o que tengas que dividir o multiplicar. Sin importar el proceso que uses, siempre deberás encontrar una manera de aislar x a un lado de la ecuación para encontrar su valor. Sigue leyendo para saber cómo hacerlo.

Parte 1
Parte 1 de 5:
Utilizar una ecuación lineal básica

  1. Imagen titulada Solve for X Step 1
    1
    Escribe el problema. Aquí está:
    • 22(x+3) + 9 - 5 = 32
  2. Imagen titulada Solve for X Step 2
    2
    Resuelve el exponente. Recuerda el orden de las operaciones: PEMDAS (paréntesis, exponentes, multiplicación o división y adición o sustracción). No puedes resolver antes el paréntesis porque x está dentro del paréntesis, así que debes empezar con el exponente, 22. 22 = 4
    • 4(x+3) + 9 - 5 = 32
  3. Imagen titulada Solve for X Step 3
    3
    Haz la multiplicación. Solo distribuye el 4 en (x + 3). De esta manera:
    • 4x + 12 + 9 - 5 = 32
  4. Imagen titulada Solve for X Step 4
    4
    Haz la adición y la sustracción. Solo suma o resta el resto de los números. De esta manera:
    • 4x+21-5 = 32
    • 4x+16 = 32
    • 4x + 16 - 16 = 32 - 16
    • 4x = 16
  5. Imagen titulada Solve for X Step 5
    5
    Aísla la variable. Para hacerlo, solo divide ambos lados de la ecuación por 4 para encontrar x. 4x/4 = x y 16/4 = 4, así x = 4.
    • 4x/4 = 16/4
    • x = 4
  6. Imagen titulada Solve for X Step 6
    6
    Comprueba tu trabajo. Solo reemplaza x por 4 en la ecuación original para asegurar que esté bien. De esta manera:
    • 22(x+3)+ 9 - 5 = 32
    • 22(4+3)+ 9 - 5 = 32
    • 22(7) + 9 - 5 = 32
    • 4(7) + 9 - 5 = 32
    • 28 + 9 - 5 = 32
    • 37 - 5 = 32
    • 32 = 32
    Anuncio

Parte 2
Parte 2 de 5:
Utilizar exponentes

  1. Imagen titulada Solve for X Step 7
    1
    Escribe el problema. Si trabajas con un problema en el que el término x incluye un exponente:
    • 2x2 + 12 = 44
  2. Imagen titulada Solve for X Step 8
    2
    Aísla el término con el exponente. Lo primero que debes hacer es combinar los términos semejantes de tal manera que todos los términos constantes estén al lado derecho de la ecuación mientras que el término con el exponente esté en el lado izquierdo. Solo resta 12 de ambos lados. De esta manera:
    • 2x2+12-12 = 44-12
    • 2x2 = 32
  3. Imagen titulada Solve for X Step 9
    3
    Aísla la variable con el exponente dividiendo ambos lados por el coeficiente del término x. En este caso, 2 es el coeficiente de x, así que divide ambos lados de la ecuación por 2 para deshacerte del coeficiente. De esta manera:
    • (2x2)/2 = 32/2
    • x2 = 16
  4. Imagen titulada Solve for X Step 10
    4
    Toma la raíz cuadrada de cada lado de la ecuación. Tomar la raíz cuadrada de x2 la cancelará. Así que toma la raíz cuadrada de ambos lados. Te quedará una x a un lado y la raíz cuadrada de 16, 4, al otro. Por lo tanto, x = 4.
  5. Imagen titulada Solve for X Step 11
    5
    Comprueba tu trabajo. Solo reemplaza x por 4 en la ecuación original para asegurarte de que esté bien. De esta manera:
    • 2x2 + 12 = 44
    • 2 x (4)2 + 12 = 44
    • 2 x 16 + 12 = 44
    • 32 + 12 = 44
    • 44 = 44
    Anuncio

Parte 3
Parte 3 de 5:
Utilizar fracciones

  1. Imagen titulada Solve for X Step 12
    1
    Escribe el problema. Digamos que trabajas con el siguiente problema:[1]
    • (x + 3)/6 = 2/3
  2. Imagen titulada Solve for X Step 13
    2
    Haz la regla de tres. Para hacer la regla de tres, solo multiplica el denominador de cada fracción por el numerador de la otra fracción (esencialmente, multiplica en dos líneas diagonales). Entonces, multiplica el primer denominador (6) por el segundo numerador (2) para obtener 12 al lado derecho de la ecuación. Multiplica el segundo denominador (3) por el primer numerador (x + 3) para obtener 3x + 9 al lado izquierdo de la ecuación. Debe verse de esta manera:
    • (x + 3)/6 = 2/3
    • 6 x 2 = 12
    • (x + 3) x 3 = 3x + 9
    • 3x + 9 = 12
  3. Imagen titulada Solve for X Step 14
    3
    Combina los términos semejantes. Combina los términos constantes en la ecuación para restar 9 de ambos lados. Esto es lo que debes hacer:
    • 3x + 9 - 9 = 12 - 9
    • 3x = 3
  4. Imagen titulada Solve for X Step 15
    4
    Aísla x dividiendo cada término por el coeficiente de x. Solo divide 3x y 9 por 3 (el coeficiente de x) para calcular x. 3x/3 = x y 3/3 = 1, entonces obtendrás x = 1.
  5. Imagen titulada Solve for X Step 16
    5
    Comprueba tu trabajo. Para comprobar tu trabajo, solo reemplaza x en la ecuación original para asegurarte de que funciona. Esto es lo que debes hacer:
    • (x + 3)/6 = 2/3
    • (1 + 3)/6 = 2/3
    • 4/6 = 2/3
    • 2/3 = 2/3
    Anuncio

Parte 4
Parte 4 de 5:
Utilizar signos radicales

  1. Imagen titulada Solve for X Step 17
    1
    Escribe el problema. Digamos que quieres calcular x en el siguiente problema:[2]
    • √(2x+9) - 5 = 0
  2. Imagen titulada Solve for X Step 18
    2
    Aísla la raíz cuadrada. Debes mover la parte de la ecuación con el signo de la raíz cuadrada a un lado antes de que puedas proceder. De esta manera, tendrás que sumar 5 a ambos lados de la ecuación. Debes hacerlo de esta manera:
    • √(2x+9) - 5 + 5 = 0 + 5
    • √(2x+9) = 5
  3. Imagen titulada Solve for X Step 19
    3
    Eleva al cuadrado ambos lados. Así como se divide ambos lados de una ecuación por un coeficiente que se multiplica por x, debes elevar al cuadrado ambos lados de la ecuación si x aparece bajo la raíz cuadrada o el signo radical. Esto eliminará el signo radical de la ecuación. Debes hacerlo de esta forma:
    • (√(2x+9))2 = 52
    • 2x + 9 = 25
  4. Imagen titulada Solve for X Step 20
    4
    Combina los términos semejantes. Combina los términos semejantes restando 9 de ambos lados para que todos los términos constantes estén al lado derecho de la ecuación, mientras que la x debe permanecer al lado izquierdo. Esto es lo que debes hacer:
    • 2x + 9 - 9 = 25 - 9
    • 2x = 16
  5. Imagen titulada Solve for X Step 21
    5
    Aísla la variable. Lo último que debes hacer para calcular el valor de x es aislar la variable dividiendo ambos lados de la ecuación por 2 (el coeficiente del término x). 2x/2 = x y 16/2 = 8, de esta manera obtendrás x = 8.
  6. Imagen titulada Solve for X Step 22
    6
    Comprueba tu trabajo. Reemplaza 8 por x en la ecuación original para obtener la respuesta correcta:
    • √(2x+9) - 5 = 0
    • √(2(8)+9) - 5 = 0
    • √(16+9) - 5 = 0
    • √(25) - 5 = 0
    • 5 - 5 = 0
    Anuncio

Parte 5
Parte 5 de 5:
Utilizar un valor absoluto

  1. Imagen titulada Solve for X Step 23
    1
    Escribe el problema. Digamos que tratas de calcular x en el siguiente problema:[3]
    • |4x +2| - 6 = 8
  2. Imagen titulada Solve for X Step 24
    2
    Aísla el valor absoluto. Lo primero que debes hacer es combinar los términos semejantes y lograr que los términos dentro del signo de valor absoluto estén a un lado. En este caso, debes hacerlo sumando 6 a ambos lados de la ecuación. De esta manera:
    • |4x +2| - 6 = 8
    • |4x +2| - 6 + 6 = 8 + 6
    • |4x +2| = 14
  3. Imagen titulada Solve for X Step 25
    3
    Elimina el valor absoluto y resuelve la ecuación. Este es el primer paso y el más sencillo. Tendrás que calcular la x dos veces cuando trabajes con un valor absoluto. Debes hacerlo de esta manera la primera vez:
    • 4x + 2 = 14
    • 4x + 2 - 2 = 14 -2
    • 4x = 12
    • x = 3
  4. Imagen titulada Solve for X Step 26
    4
    Elimina el valor absoluto y cambia el signo de los términos en el lado opuesto del signo igual antes de resolverlo. Ahora, hazlo de nuevo, solo que esta vez iguala la primera parte de la ecuación a -14 en vez de a 14. De esta manera:
    • 4x + 2 = -14
    • 4x + 2 - 2 = -14 - 2
    • 4x = -16
    • 4x/4 = -16/4
    • x = -4
  5. Imagen titulada Solve for X Step 27
    5
    Comprueba tu trabajo. Ahora que sabes que x = (3, -4), simplemente reemplaza ambos números en la ecuación original para saber si funciona. De esta manera:
    • (Para x = 3):
      • |4x +2| - 6 = 8
      • |4(3) +2| - 6 = 8
      • |12 +2| - 6 = 8
      • |14| - 6 = 8
      • 14 - 6 = 8
      • 8 = 8
    • (Para x = -4):
      • |4x +2| - 6 = 8
      • |4(-4) +2| - 6 = 8
      • |-16 +2| - 6 = 8
      • |-14| - 6 = 8
      • 14 - 6 = 8
      • 8 = 8
    Anuncio

Consejos

  • Los radicales o las raíces son otra manera de representar a los exponentes. La raíz cuadrada de x = x^1/2.
  • Para comprobar tu trabajo, reemplaza el valor de la x en la ecuación original y resuélvela.
Anuncio

wikiHows relacionados

calcular el diámetro de un círculo
Cómo
calcular el diámetro de un círculo
calcular un incremento en porcentaje
Cómo
calcular un incremento en porcentaje
calcular la variación porcentual
Cómo
calcular la variación porcentual
medir milímetros
Cómo
medir milímetros
calcular una frecuencia
Cómo
calcular una frecuencia
calcular las probabilidades de sacarte la lotería
Cómo
calcular las probabilidades de sacarte la lotería
convertir de grados a radianes
Cómo
convertir de grados a radianes
calcular la incertidumbre
Cómo
calcular la incertidumbre
calcular la varianza
Cómo
calcular la varianza
convertir radianes a grados
Cómo
convertir radianes a grados
calcular la velocidad
Cómo
calcular la velocidad
calcular el porcentaje de error
Cómo
calcular el porcentaje de error
encontrar una raíz cuadrada sin una calculadora
Cómo
encontrar una raíz cuadrada sin una calculadora
convertir de decimal a binario
Cómo
convertir de decimal a binario
Anuncio

Referencias

  1. ↑ http://www.decodedscience.com/cross-multiply-to-solve-equations-with-fractions/25496
  2. ↑ http://www.mathsisfun.com/algebra/radical-equations-solving.html
  3. ↑ http://www.sosmath.com/algebra/solve/solve0/solve0.html

Acerca de este wikiHow

David Jia
Coescrito por:
David Jia
Tutor de matemáticas
Este artículo fue coescrito por David Jia. David Jia es tutor académico y el fundador de LA Math Tutoring, una empresa de tutoría privada con sede en Los Ángeles, California. Con más de 10 años de experiencia en enseñanza, David trabaja con estudiantes de todas las edades y grados en diversas materias, así como en asesoría para postulaciones universitarias y preparación para pruebas como el SAT, ACT, ISEE y más. Luego de obtener una calificación perfecta de 800 en matemáticas y 690 en inglés en el SAT, David recibió la beca Dickinson de la Universidad de Miami, donde se graduó con una licenciatura en Administración de Empresas. Asimismo, ha trabajado como instructor para videos en línea para empresas de libros de texto como Larson Texts, Big Ideas Learning y Big Ideas Math. Este artículo ha sido visto 673 514 veces.
Categorías: Matemáticas
Anuncio