Nuestro equipo de editores e investigadores capacitados han sido autores de este artículo y lo han validado por su precisión y amplitud.
wikiHow's Content Management Team revisa cuidadosamente el trabajo de nuestro personal editorial para asegurar que cada artículo cumpla con nuestros altos estándares de calidad.
Este artículo ha sido visto 934 178 veces.
La varianza es una medida de qué tan disperso es un conjunto de datos. Es útil al momento de crear modelos estadísticos debido a que la varianza baja puede ser una señal de que estás sobreajustando tus datos. Calcular la varianza puede ser complicado, pero una vez que aprendas la fórmula, solo necesitarás introducir los números correctos para hallar la respuesta.
Pasos
Método 1
Método 1 de 2:Calcular la varianza de una muestra
-
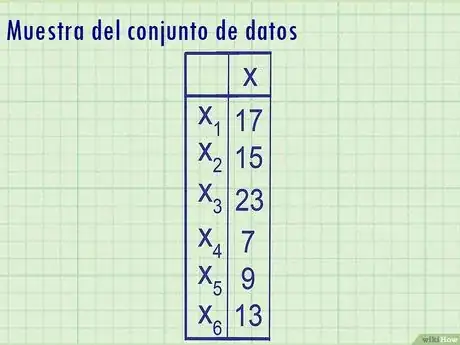
1Toma nota de la muestra del conjunto de datos. En la mayoría de los casos, los estadísticos solo tienen acceso a una muestra o a un subconjunto de la población que van a analizar. Por ejemplo, en vez de analizar la población "costo de todos los autos de Alemania", un estadístico averiguaría el costo de una muestra aleatoria de unos pocos miles de autos. De este modo podría basarse en esa muestra para obtener una estimación aproximada del costo de los autos en Alemania, aunque es posible que no coincida con el valor exacto.
- Ejemplo: analizando la cantidad de panquecitos que se venden todos los días en una cafetería, tomas una muestra de seis días aleatorios y obtienes los siguientes resultados: 17, 15, 23, 7, 9, 13. Esta es una muestra, no la población, ya que no tienes los datos de todos y cada uno de los días en los cuales ha estado abierta la cafetería.
- Si tienes todos los puntos de datos de una población, continúa con el próximo método.
-
2Anota la fórmula de la varianza de una muestra. La varianza de un conjunto de datos te indica qué tan dispersos están los puntos de datos. Mientras más cerca de cero esté la varianza, más cercanos estarán entre sí los puntos de datos. Cuando vayas a trabajar con muestras de conjuntos de datos, utiliza la siguiente fórmula para calcular la varianza:[1]
- = ∑[( - x̅)]/(n - 1)
- es la varianza. La varianza siempre se mide en unidades elevadas al cuadrado.
- representa un término de tu conjunto de datos.
- ∑, que significa "sumatoria", te indica que debes calcular los siguientes términos para cada valor de y luego sumarlos a todos.
- x̅ es la media de la muestra.
- n es la cantidad de puntos de datos.
-
3Calcula la media de la muestra. El símbolo x̅ o "x barra" se refiere a la media de la muestra.[2] Calcúlala como lo calcularías cualquier media: suma todos los puntos de datos, luego divídela por la cantidad de puntos de datos.
-
Por ejemplo: primero suma todos los puntos de datos: 17 + 15 + 23 + 7 + 9 + 13 = 84
A continuación, divide la respuesta por la cantidad de puntos de datos, en este caso, seis: 84 ÷ 6 = 14.
Media de la muestra = x̅ = 14. - Puedes pensar en la media como el "punto central" de los datos. Si los datos se agrupan cerca de la media, entonces la varianza será baja. Si se encuentran esparcidos lejos de la media, la varianza será alta.
-
Por ejemplo: primero suma todos los puntos de datos: 17 + 15 + 23 + 7 + 9 + 13 = 84
-
4Réstale la media a cada punto de datos. Ahora es momento de calcular - x̅, donde es cada número del conjunto de datos. Cada respuesta te indicará la desviación con respecto de la media o, en lenguaje coloquial, qué tan lejos de la media está cada número.[3] .
-
Ejemplo:
- x̅ = 17 - 14 = 3
- x̅ = 15 - 14 = 1
- x̅ = 23 - 14 = 9
- x̅ = 7 - 14 = -7
- x̅ = 9 - 14 = -5
- x̅ = 13 - 14 = -1 - Es fácil revisar tu trabajo, ya que la suma de las respuestas debe ser igual a cero. Esto se debe justamente a la definición de la media, ya que las respuestas negativas (distancia de los números pequeños respecto de la media) cancelan exactamente las respuestas positivas (distancia de los números más grandes respecto de la media).
-
Ejemplo:
-
5Eleva cada resultado al cuadrado. Tal como se explicó más arriba, la lista actual de desviaciones ( - x̅) suman cero. Esto quiere decir que la "desviación promedio" siempre será igual a cero. Por lo tanto, esto no te dice demasiado acerca de qué tan dispersos están los datos. Para resolver este problema, debes elevar al cuadrado cada desviación. Al hacerlo, todos los números se convertirán en positivos, por lo tanto, los valores positivos y negativos dejarán de cancelarse y sumar cero.[4]
-
Ejemplo:
( - x̅)
- x̅)
92 = 81
(-7)2 = 49
(-5)2 = 25
(-1)2 = 1 - Ahora tienes el valor ( - x̅) para cada punto de datos de tu muestra.
-
Ejemplo:
-
6Calcula la suma de los valores al cuadrado. Ahora es momento de calcular el numerador total de la fórmula ∑[( - x̅)]. La letra sigma mayúscula, ∑, te indica que debes sumar el valor del siguiente término para cada valor de . Ya calculaste ( - x̅) para cada valor de en la muestra. Así que todo lo que tienes que hacer ahora, es sumar los resultados.
- Ejemplo: 9 + 1 + 81 + 49 + 25 + 1 = 166.
-
7Divide por , donde es la cantidad de puntos de datos. Hace mucho tiempo, los estadísticos dividían la varianza de la muestra por . Esto te da el valor promedio de la desviación al cuadrado, que coincide perfectamente con la varianza de la muestra. Pero recuerda que la muestra es solo una estimación de una población más grande. Si tomas otra muestra aleatoria y haces el mismo cálculo, obtendrás un resultado diferente. Por este motivo, al dividir por en vez de por obtendrás una mejor estimación de la varianza de una población más grande y eso es justamente lo que estás buscando. Esta corrección es tan común que se ha convertido en la definición aceptada de la varianza de una muestra.[5]
-
Ejemplo: en la muestra hay seis puntos de datos, por lo tanto:
Varianza de la muestra = 33,2
-
Ejemplo: en la muestra hay seis puntos de datos, por lo tanto:
-
8Aprende a distinguir varianza de desviación estándar. Ten en cuenta que, al haber un exponente en la fórmula, la varianza se mide en unidades al cuadrado de los datos originales. Esto puede hacer que no sea tan sencillo entenderlo en forma intuitiva. En su lugar, a menudo se usa la desviación estándar. De todas formas, tu esfuerzo no fue en vano, ya que la desviación estándar no es otra cosa que la raíz cuadrada de la varianza. Es por eso que la varianza de una muestra se expresa como y la desviación estándar de una muestra como .
- Por ejemplo, la desviación estándar de la muestra anterior es = s = √33,2 = 5,76.
Método 2
Método 2 de 2:Calcular la varianza de una población
-
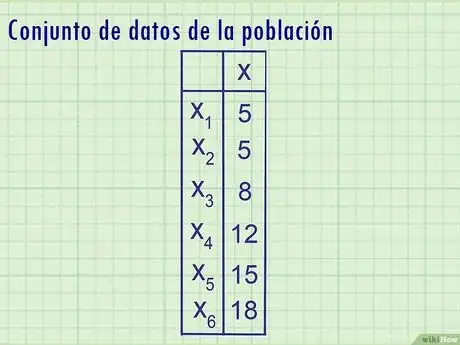
1Comienza con un conjunto de datos de la población. El término "población" hace referencia al total de datos de las observaciones relevantes. Por ejemplo, si vas a analizar la edad de los residentes del estado de Texas, tu población debe incluir la edad de cada uno de los residentes de Texas. Normalmente, para un conjunto de datos tan grande como ese, crearías una hoja de cálculo. Sin embargo, aquí tienes un conjunto más pequeño de datos como ejemplo:
-
Ejemplo: en la habitación de un acuario hay exactamente 6 peceras. Las seis peceras contienen la siguiente cantidad de peces:
-
Ejemplo: en la habitación de un acuario hay exactamente 6 peceras. Las seis peceras contienen la siguiente cantidad de peces:
-
2Anota la fórmula de la varianza de la población. Debido a que la población contiene todos los datos que necesitas, esta fórmula te dará el valor exacto de la varianza de la población. Para poder distinguirla de la varianza de una muestra (que es solo un valor aproximado), los estadísticos usan otras variables:[6]
- σ = (∑( - μ))/n
- σ = varianza de la población. Es la letra sigma minúscula, elevada al cuadrado. La varianza se mide en unidades al cuadrado.
- representa un término de tu conjunto de datos.
- Los términos dentro de ∑ se calcularán para cada valor de , y luego se sumarán.
- μ es la media de la población.
- n es la cantidad de puntos de datos de la población.
-
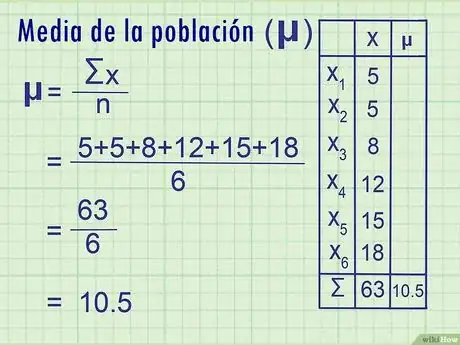
3Encuentra la media de la población. Cuando analizas una población, el símbolo μ ("mu") representa la media aritmética. Para encontrar la media, suma todos los puntos de datos y luego divide el resultado por la cantidad de puntos de datos.
- Puedes pensar en la media como el "promedio", pero ten cuidado, ya que esa palabra tiene muchas definiciones en matemática.
- Ejemplo: media = μ = = 10,5
-
4Réstale la media a cada punto de datos. Los puntos de datos cercanos a la media tendrán una diferencia más cercana a cero. Repite la resta para cada punto de datos y comenzarás a tener una noción aproximada de qué tan dispersos están los datos.
-
Ejemplo:
- μ = 5 - 10,5 = -5,5
- μ = 5 - 10,5 = -5,5
- μ = 8 - 10,5 = -2,5
- μ = 12 - 10,5 = 1,5
- μ = 15 - 10,5 = 4,5
- μ = 18 - 10,5 = 7,5
-
Ejemplo:
-
5Eleva al cuadrado todas las respuestas. Ahora, algunos de los números del paso anterior serán negativos mientras que otros serán positivos. Si dibujas tus datos en una línea numérica, estas dos categorías representarán los números que están a la izquierda de la media y los que están a la derecha de la media. Estos valores no son de mucha ayuda para calcular la varianza, ya que los dos grupos se cancelarían entre sí. Eleva al cuadrado cada uno de los números para transformarlos en valores positivos.
-
Ejemplo:
( - μ) para cada valor de i de 1 a 6:
(-5,5) = 30,25
(-5,5) = 30,25
(-2,5) = 6,25
(1,5) = 2,25
(4,5) = 20,25
(7,5) = 56,25
-
Ejemplo:
-
6Encuentra la media de tus resultados. Ahora tienes un valor para cada punto de datos, relacionado (indirectamente) con la dispersión que ese punto de datos tiene respecto de la media. Calcula la media de estos valores sumándolos y luego dividiendo la suma por la cantidad de valores.
-
Ejemplo:
Varianza de la población = 24,25
-
Ejemplo:
-
7Relaciona este valor nuevamente con la fórmula. Si no estás seguro acerca de cómo coincide este valor con la fórmula que aplicaste al principio de este método, intenta escribir todo el problema a mano:
- Después de encontrar la diferencia entre la media y elevar al cuadrado, obtendrás el valor ( - μ), ( - μ), y así sucesivamente hasta ( - μ), donde es el último punto de datos del conjunto.
- Para encontrar la media de estos valores, debes sumarlos a todos y dividirlos por : ( ( - μ) + ( - μ) + ... + ( - μ) ) / n
- Después de rescribir el numerador en notación sigma, obtendrás (∑( - μ))/n, que es la fórmula de la varianza.
Consejos
- Debido a que es difícil interpretar la varianza, este valor generalmente se calcula como punto de partida para el cálculo de la desviación estándar.
- La utilización de en lugar de en el denominador al analizar muestras, es una técnica conocida como corrección de Bessel. La muestra es solo un valor estimativo de la población completa y la media de la muestra se encuentra sesgada para ajustar esa estimación. Esta corrección sirve para eliminar ese sesgo. Esto tiene que ver con el hecho de que, una vez que hayas listado los puntos de datos, el n-ésimo punto final ya tendrá una restricción, dado que solamente algunos valores resultarán en la media de la muestra (x̅) utilizada en la fórmula de la varianza.[7]
Referencias
- ↑ https://www.youtube.com/watch?v=VgKHjVDK0uM
- ↑ http://stattrek.com/statistics/notation.aspx
- ↑ http://www.mathsisfun.com/data/standard-deviation.html
- ↑ https://www.youtube.com/watch?v=sOb9b_AtwDg
- ↑ https://www.youtube.com/watch?v=sOb9b_AtwDg
- ↑ https://www.youtube.com/watch?v=VgKHjVDK0uM
- ↑ http://www.statsdirect.com/help/default.htm#basics/degrees_freedom.htm
Acerca de este wikiHow
Para calcular la varianza, primero calcula la media (o promedio) de la muestra. Luego réstale a cada punto de dato la media y eleva esta diferencia al cuadrado. Posteriormente, suma todas las diferencias al cuadrado. Por último, divide el resultado de la suma entre n menos 1, siendo n la cantidad total de puntos de datos de la muestra. ¡Desplázate hacia abajo si quieres aprender a calcular la varianza de una población!







































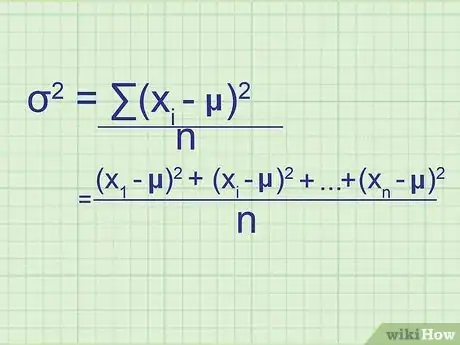



















wikiHow's Content Management Team revisa cuidadosamente el trabajo de nuestro personal editorial para asegurar que cada artículo cumpla con nuestros altos estándares de calidad. Este artículo ha sido visto 934 178 veces.