Nuestro equipo de editores e investigadores capacitados han sido autores de este artículo y lo han validado por su precisión y amplitud.
wikiHow's Content Management Team revisa cuidadosamente el trabajo de nuestro personal editorial para asegurar que cada artículo cumpla con nuestros altos estándares de calidad.
Este artículo ha sido visto 196 669 veces.
Todos han escuchado comparaciones entre las probabilidades de ganar la lotería y las probabilidades de otros eventos poco probables (por ejemplo, que te caiga un rayo). Si bien es verdad que las probabilidades de ganar el bote en un juego como el Powerball u otro juego de lotería de selección de 6 números son extremadamente bajas, ¿qué tan bajas son? ¿Y cuántas veces tendrías que jugar para tener mejores posibilidades de ganar? Puedes encontrar estas respuestas hasta las probabilidades exactas con algunos cálculos simples.
Pasos
Método 1
Método 1 de 3:Calcular las probabilidades de ganar el bote del Powerball
-
1Comprende los cálculos involucrados. Si quieres determinar las probabilidades de ganar cualquier lotería, divide la cantidad de números ganadores entre la cantidad total de números posibles. En caso de que los números se elijan de un conjunto y el orden no importe, utiliza la fórmula . En la fórmula, n representa la cantidad total de números posibles y r representa la cantidad de números elegidos. El signo "!" denota un factorial, el cual, para cualquier número entero n es n*(n - 1)*( n - 2)... y así sucesivamente hasta llegar a 0. Por ejemplo, 3! representa .[1]
- Si quieres un ejemplo simple, imagina que debes elegir dos números y puedes elegir números del 1 al 5. Tus probabilidades de elegir los dos números "correctos" (los números ganadores) se definiría como .
- Luego, esto se resolvería de la siguiente forma: , que es , o 10.
- Por lo tanto, tus probabilidades de ganar este juego son de 1 en 10.
- Los cálculos con factoriales pueden volverse difíciles de manejar, sobre todo con números grandes. En su mayoría, las calculadoras tienen una función de factorial para que los cálculos te sean más fáciles. Como otra alternativa, puedes escribir el factorial en Google (por ejemplo, como "55!") y te lo resolverá.
-
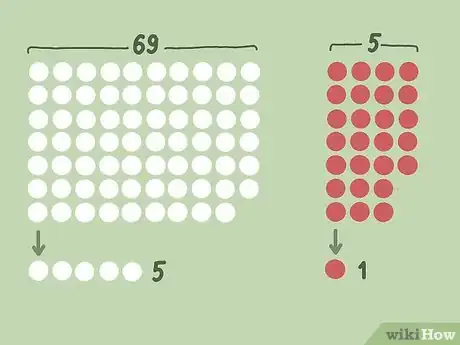
2Establece las reglas de la lotería. La mayoría de las loterías como Mega Millions, Powerball y otras loterías grandes utilizan aproximadamente las mismas reglas: se eligen 5 o 6 números de un grupo grande de números sin un orden particular. No es posible repetir los números. En algunos juegos, se elige un número final de un conjunto de números más pequeño (un ejemplo es el número "Powerball" en los juegos de Powerball). En el Powerball, se eligen 5 números de 69 números posibles. Luego, para el número Powerball único, se elige un número de un conjunto de 26 números posibles.[2]
- Es posible que otros juegos te hagan elegir 5 o 6 números, o más de un grupo de números más grande o pequeño. Si quieres calcular las probabilidades de ganar, tan solo debes saber la cantidad de números ganadores y la cantidad total de números posibles.[3]
-
3Ingresa los números en la ecuación de probabilidad. La primera parte de las probabilidades del Powerball determina la cantidad de formas en las que se podrían elegir 5 números de 69 números únicos. Usando las reglas del Powerball, la ecuación completada para los primeros 5 números sería , que se simplifica a .[4]
-
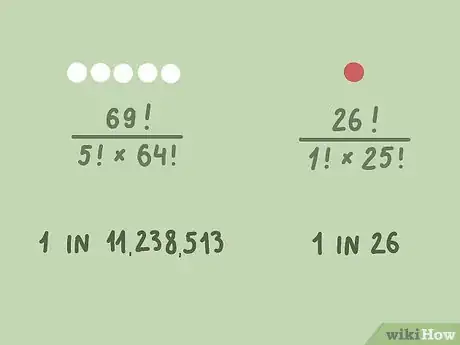
4Calcula tus probabilidades de elegir correctamente. Para resolver esta ecuación, lo mejor es hacerlo en su totalidad en un motor de búsqueda o calculadora debido a que es inconveniente anotar los números involucrados entre cada paso. El resultado te indica que hay 11 238 513 combinaciones posibles de 5 números en un conjunto de 69 números únicos. Esto quiere decir que tus probabilidades son de 1 en 11 238 513 de elegir los cinco números correctamente.[5]
- Si quieres calcular tus probabilidades de elegir el número final Powerball correctamente, completarías la misma ecuación usando los valores para el Powerball (1 número de entre 26 números posibles). Debido a que aquí solo eliges un número, no necesariamente debes completar toda la ecuación. La respuesta será 26, ya que hay 26 maneras distintas en las que se puede elegir un número de un conjunto de 26 números únicos.
-
5Multiplica para calcular tus probabilidades de ganar el bote. Si quieres calcular las probabilidades de que adivinarás los 5 primeros números y el número Powerball correctamente para ganar el bote, multiplica las probabilidades de que adivinarás los primeros 5 números (1 en 11 238 513) por las probabilidades de que adivinarás correctamente el número Powerball (1 en 26). La ecuación sería .[6]
- Entonces, tus probabilidades de elegir correctamente los 5 primeros números y el número Powerball y ganar el bote son de 1 en 292 201 338.
Anuncio
Método 2
Método 2 de 3:Determinar las probabilidades para los premios menores
-
1Calcula tus probabilidades de ganar el segundo premio. Volviendo al juego del Powerball, hay 5 números y un solo número Powerball. En caso de que adivines los 5 números restantes correctamente pero no obtengas el número Powerball, ganarás el segundo premio. Si calculaste tus probabilidades de ganar el bote, de por sí sabes que tus probabilidades de adivinar los 5 números correctamente son de 1 en 11 238 513.[7]
- Para ganar el segundo premio, tendrías que adivinar el número Powerball incorrectamente. En caso de que hayas calculado tus probabilidades de ganar el bote, sabes que tus probabilidades de adivinar el número Powerball correctamente son de 1 en 26. Por ende, tus probabilidades adivinar el número Powerball incorrectamente son de 25 en 26.
- Utiliza la misma ecuación con estos valores para determinar tus probabilidades de ganar el segundo premio: . Al terminar este cálculo, verás que tus probabilidades de ganar el segundo premio son de 1 en 11 688 053,52.
-
2Usa una ecuación expandida para encontrar tus probabilidades de ganar otros premios. Para ganar otros premios, adivinas correctamente algunos de los números ganadores, pero no todos. Si quieres determinar tus probabilidades, usa una ecuación en la que "k" represente los números que elijas correctamente, "r" represente la cantidad total de números que se obtuvieron y "n" represente la cantidad de números únicos de los cuales se tomarán los números. Sin los números, la fórmula se ve así: .
- Por ejemplo, podrías usar los valores del Powerball para determinar tus probabilidades de adivinar correctamente 3 de los 5 números elegidos del conjunto de 69 números únicos. La ecuación se vería así: .
- El resultado de esta ecuación te indica la cantidad de formas en las que se pueden elegir 3 números correctamente de 5 números. Tus probabilidades serán ese número de la cantidad total de formas en las que se pueden elegir 5 números correctamente.
-
3Resuelve la ecuación para encontrar las probabilidades de adivinar los números correctamente. Al igual que con la ecuación base, lo mejor es resolver esta ecuación tecleándola toda en una calculadora o motor de búsqueda. Sería engorroso anotar algunos de los números intermedios involucrados en el cálculo y sería fácil cometer un error.[8]
- En el ejemplo anterior, tus probabilidades de adivinar 3 de los 5 números elegidos en el Powerball serían de 20 160 en 11 238 513.
-
4Multiplica el resultado por el valor del número Powerball para determinar tus probabilidades de ganar ese premio. Esta fórmula te da las probabilidades de adivinar correctamente solo algunos de los números, pero aún no has tomado en consideración el número Powerball. Si quieres encontrar tus probabilidades verdaderas, multiplica el resultado por las probabilidades de adivinar correcta o incorrectamente el número Powerball (el valor que quieras obtener).[9]
- Por ejemplo, si quieres calcular tus probabilidades de adivinar correctamente solo 3 de los 5 números y no acertar en el número Powerball, la ecuación sería , o de 1 en 579,76.
- Por otro lado, las probabilidades de adivinar correctamente 3 de los 5 números y acertar en el número Powerball serían , o de 1 en 14 494,11.
-
5Cambia la cantidad de números que hayas adivinado correctamente para otros premios. Después de dominar la fórmula, tan solo cambia el valor de "k" para encontrar las probabilidades de ganar premios de distintos niveles. En general, tus probabilidades de ganar disminuirán conforme el valor de "k" incremente.[10]
- En caso de que vayas a calcular las probabilidades del Powerball o un juego similar, recuerda multiplicar el resultado por el valor del Powerball.
Anuncio
Método 3
Método 3 de 3:Calcular las probabilidades de ganar otras loterías
-
1Busca el retorno esperado de un boleto de lotería. El retorno esperado te indica lo que podrías esperar recuperar en teoría por comprar un solo boleto de lotería. Si quieres calcular el retorno esperado de un solo boleto, multiplica las probabilidades de un pago en particular por el valor de ese pago. Si lo haces para cada premio que podrías ganar, obtendrás un rango de retornos esperados.[11]
- Volviendo al ejemplo del Powerball, el retorno esperado de un solo boleto de $2 sería de alrededor de $1,79 en el extremo alto y de apenas $1,35 en el extremo bajo.
- Ten en cuenta que "retorno esperado" es un término de arte que se utiliza en la estadística. El pago real casi siempre será mucho menor que el retorno esperado que hayas calculado.
-
2Compara el costo de un solo boleto con su retorno esperado. Puedes determinar el beneficio esperado de jugar la lotería si comparas el retorno esperado de un boleto con el costo. La mayor parte del tiempo, el retorno esperado será menor al costo del boleto. Adicionalmente, es probable que el retorno en sí difiera en gran medida del valor esperado. Por lo general, obtendrás únicamente una fracción del valor esperado, si acaso.[12]
- Calcular las probabilidades puede servirte para determinar los juegos de lotería que tengan el mejor beneficio esperado. Por ejemplo, en un momento, la New York Lottery tenía un boleto Take Five ("lleva cinco") de $1 cuyo valor esperado era equivalente a su costo. Si lo jugabas, podías esperar cubrir tus pérdidas con el tiempo.[13]
-
3Determina el incremento en las probabilidades al jugar varias veces. Jugar la lotería varias veces hace que tus probabilidades generales de ganar sean mayores, por muy pocas que sean. Es más fácil visualizar este incremento como una disminución en tus probabilidades de perder.[14]
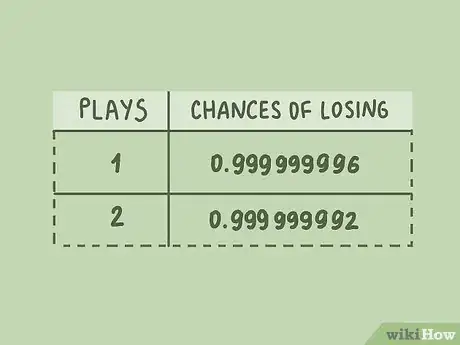
- Por ejemplo, en caso de que tus probabilidades generales de ganar sean de 1 en 250 000 000, tus probabilidades de perder en una jugada son de . Esto equivale a un número muy cercano a 1 (0,99999...).
- En caso de que juegues dos veces, ese número se eleva al cuadrado (), lo que representa un alejamiento ligero de 1 (y, por ende, mejores probabilidades de ganar).
-
4Busca la cantidad de jugadas que se necesitan para tener probabilidades considerables de ganar. En su mayoría, quienes juegan la lotería están convencidos de que, si juegan con la frecuencia suficiente, tendrán probabilidades significativamente mayores de ganar. Si bien es cierto que jugar más incrementa las probabilidades de ganar, toma mucho tiempo para que ese incremento en las probabilidades se vuelva significativo.[15]
- Por ejemplo, si tuvieras una probabilidad de 1 en 250 000 000 de ganar en una jugada, tomaría alrededor de 180 millones de jugadas para llegar a una probabilidad de ganar del 50-50.
- A este ritmo, si compraras 10 boletos al día por 49 300 años, tendrías una probabilidad de ganar del 50 %.
- Asimismo, en caso de que por fin llegaras a las probabilidades de 50-50, de todos modos, no estaría garantizado que ganes si compraras dos boletos ese día. Tus probabilidades generales de ganar seguirían siendo de aproximadamente el 50 % para cada uno de esos boletos.
Anuncio
Consejos
- Cualquier conjunto de números tiene exactamente las mismas probabilidades que cualquier otro. 32-45-22-19-09-11 es igual a 1-2-3-4-5-6.
Advertencias
- Evita apostar más de lo que puedas perder.
- No caigas en estafas de lotería en las que alguien te dice que tiene una manera infalible de ganar. Si alguien tuviera una manera infalible y garantizada de ganar, sería contraproducente que te la contara.
- En caso de que consideres que tienes un problema con el juego, es probable que así sea. Jugadores Anónimos es una buena fuente de información y ayuda para quienes sufran de una adicción al juego.
Referencias
- ↑ http://garsia.math.yorku.ca/~zabrocki/math5020f03/lot649/lot649v3.pdf
- ↑ http://www.flalottery.com/exptkt/pwrball-odds.pdf
- ↑ http://garsia.math.yorku.ca/~zabrocki/math5020f03/lot649/lot649v3.pdf
- ↑ http://www.molottery.com/powerball/understanding_chances.jsp
- ↑ http://www.molottery.com/powerball/understanding_chances.jsp
- ↑ http://www.flalottery.com/exptkt/pwrball-odds.pdf
- ↑ http://www.flalottery.com/exptkt/pwrball-odds.pdf
- ↑ http://www.flalottery.com/exptkt/pwrball-odds.pdf
- ↑ http://www.flalottery.com/exptkt/pwrball-odds.pdf
- ↑ http://garsia.math.yorku.ca/~zabrocki/math5020f03/lot649/lot649v3.pdf
- ↑ https://www.wired.com/2016/01/the-fascinating-math-behind-why-you-wont-win-powerball/
- ↑ https://www.wired.com/2016/01/the-fascinating-math-behind-why-you-wont-win-powerball/
- ↑ http://wmbriggs.com/post/5285/
- ↑ http://www.quickanddirtytips.com/education/math/what-are-the-odds-of-winning-the-lottery
- ↑ http://www.quickanddirtytips.com/education/math/what-are-the-odds-of-winning-the-lottery










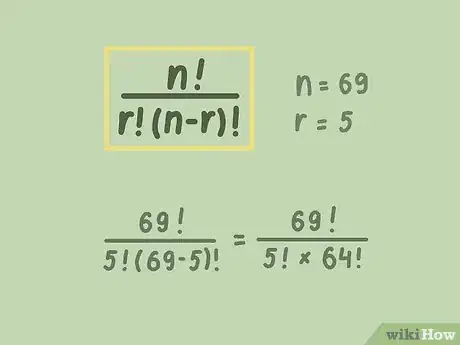






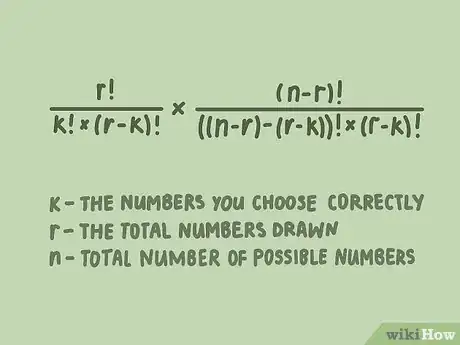






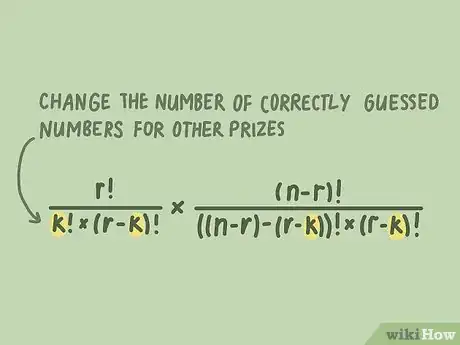


















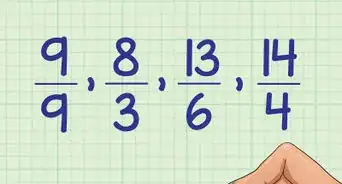





wikiHow's Content Management Team revisa cuidadosamente el trabajo de nuestro personal editorial para asegurar que cada artículo cumpla con nuestros altos estándares de calidad. Este artículo ha sido visto 196 669 veces.