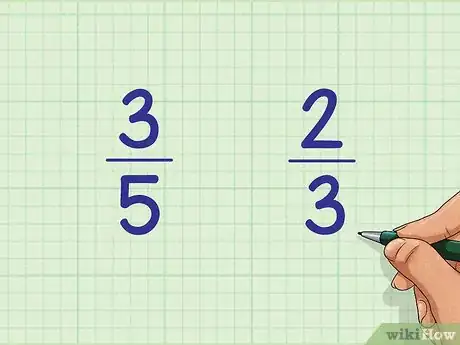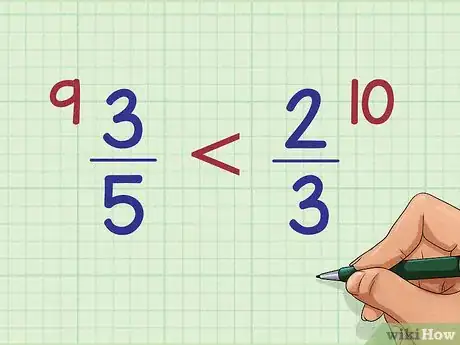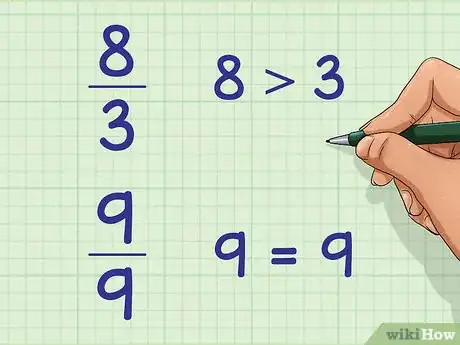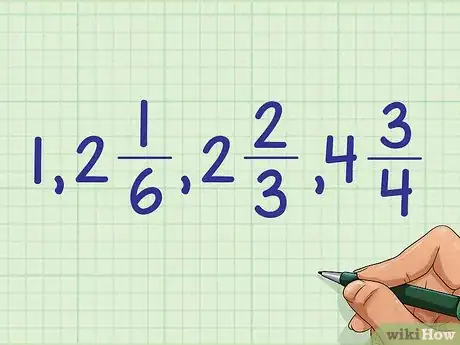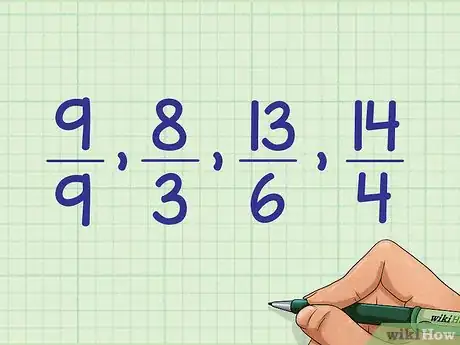Cómo ordenar fracciones de menor a mayor

Coescrito por David Jia

Si bien es fácil ordenar los números enteros como 1, 3 y 8 por tamaño, las fracciones pueden ser difíciles de medir a primera vista. Si cada número menor, o denominador, es el mismo, puedes ordenarlos como números enteros, por ejemplo: 1/5, 3/5 y 8/5. De lo contrario, puedes alterar tu lista de fracciones para usar el mismo denominador sin cambiar el tamaño de ninguna de ellas. Será más fácil con la práctica y también podrás aprender un par de trucos cuando compares dos fracciones o cuando resuelvas fracciones “impropias” con un número de arriba muy grande como 7/3.

Método 1

Método 1 de 3:
Ordenar cualquier número de fracciones

1
Busca el común denominador para todas las fracciones. Emplea algunos de los métodos que te presentaremos para buscar el denominador, o el número más bajo de una fracción, que podrás usar para volver a escribir todas las fracciones de la lista y puedas compararlas fácilmente. A esto se le denomina el común denominador, o el mínimo común denominador, si es el menor posible:^{[1]
X
Fuente de investigación}
- Multiplica todos los denominadores diferentes. Por ejemplo, si vas a comparar 2/3, 5/6 y 1/3, multiplica los dos denominadores diferentes: 3 x 6 = 18. Este método es simple, pero por lo general brinda un número mucho más grande que los demás métodos, con el cual podría ser más difícil trabajar.
- Si no, haz una lista de los múltiplos de cada denominador en una columna separada hasta que observes el número que se repita en todas las columnas. Usa ese número. Por ejemplo, para comparar 2/3, 5/6 y 1/3, haz una lista de unos cuantos múltiplos de 3: 3, 6, 9, 12, 15, 18. Luego, haz una lista de los múltiplos de 6: 6, 12, 18. Como 18 aparece en ambas listas, tendrás que usar ese número.
2
Convierte cada fracción de modo que use el común denominador. Recuerda: si multiplicas la parte de arriba y la parte de abajo de una fracción por el mismo número, la fracción seguirá teniendo el mismo tamaño. Emplea esta técnica en cada fracción, una por una, de modo que el número de abajo de cada una de las fracciones sea el común denominador. Pruébalo para 2/3, 5/6 y 1/3 usando el común denominador 18:
- 18 ÷ 3 = 6, entonces 2/3 = (2x6)/(3x6)=12/18
- 18 ÷ 6 = 3, entonces 5/6 = (5x3)/(6x3)=15/18
- 18 ÷ 3 = 6, entonces 1/3 = (1x6)/(3x6)=6/18
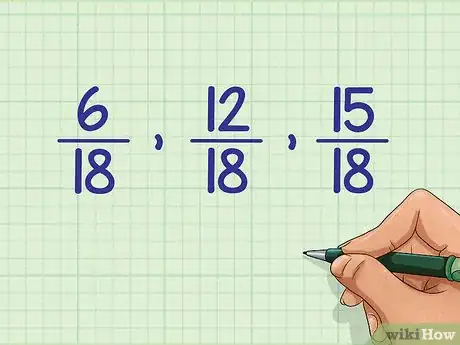
3
Utiliza el número de arriba para ordenar las fracciones. Ahora que todas tienen el mismo denominador, será fácil compararlas. Usa el número de arriba, o numerador, para ordenarlas de menor a mayor. Al ordenar las fracciones del ejemplo anterior, obtuvimos lo siguiente: 6/18, 12/18, 15/18.
4
Vuelve a convertir cada fracción a su forma original. Mantén las fracciones en el mismo orden, pero vuélvelas a convertir a su forma original. Podrás hacerlo recordando cómo transformaste cada fracción o dividiendo la parte de arriba y de abajo de cada fracción nuevamente:
- 6/18 = (6 ÷ 6)/(18 ÷ 6) = 1/3
- 12/18 = (12 ÷ 6)/(18 ÷ 6) = 2/3
- 15/18 = (15 ÷ 3)/(18 ÷ 3) = 5/6
- La respuesta es “1/3, 2/3, 5/6”.
Anuncio

Método 2

Método 2 de 3:
Ordenar dos fracciones empleando la multiplicación cruzada

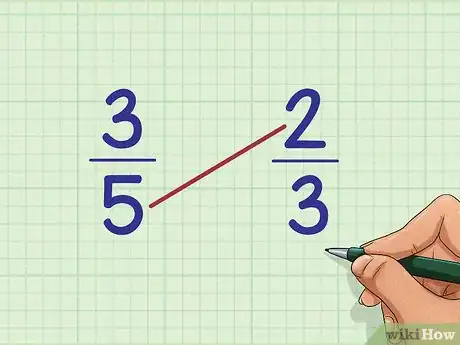
1
Escribe dos fracciones una al lado de la otra. Por ejemplo, compara la fracción 3/5 y la fracción 2/3. Escríbelas lado al lado en una página: 3/5 a la izquierda y 2/3 a la derecha.
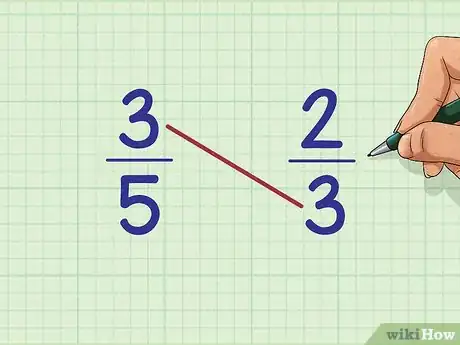
2
Multiplica el número de arriba de la primera fracción con el número de abajo de la segunda fracción. En nuestro ejemplo, el número de arriba, o numerador, de la primera fracción (3/5) es 3. El número de abajo, o denominador, de la segunda fracción (2/3) también es 3. Multiplícalos: 3 x 3 = ?
- A este método se le denomina multiplicación cruzada, porque los números se multiplican en diagonal entre sí.
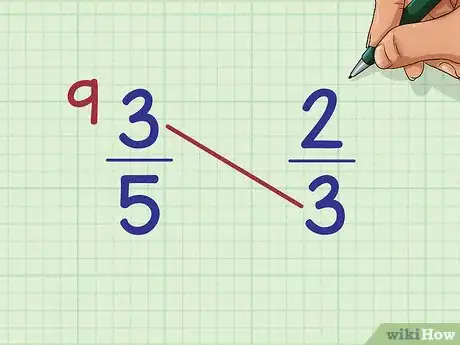
3
Anota la respuesta al lado de la primera fracción. Anota el producto, o la respuesta del problema de multiplicación, al lado de la primera fracción de la página. En nuestro ejemplo: 3 x 3 = 9, así que deberás escribir 9 al lado de la primera fracción ubicada a la mano izquierda de la página.
4
Multiplica el número de arriba de la segunda fracción por el número de abajo de la primera. Para descubrir qué fracción es mayor, tendremos que comparar nuestra respuesta anterior con la respuesta a otro problema de multiplicación. Multiplica estos dos números. Para nuestro ejemplo (la comparación de 3/5 y 2/3), multiplica 2 x 5.
5
Escribe esta respuesta al lado de la segunda fracción. Escribe la respuesta de este segundo problema de multiplicación al lado de la segunda fracción. En este ejemplo, la respuesta es 10.
6
Compara los valores de los dos productos cruzados. Las respuestas a los problemas de multiplicación en este método se denominan productos cruzados. Si un producto cruzado es mayor al otro, entonces la fracción que se ubica al lado de ese producto cruzado también será mayor a la otra fracción. En nuestro ejemplo, como 9 es menor a 10, esto significa que 3/5 debe ser menor que 2/3.
- Recuerda que siempre debes escribir el producto cruzado al lado de la fracción cuyo número de arriba hayas empleado.
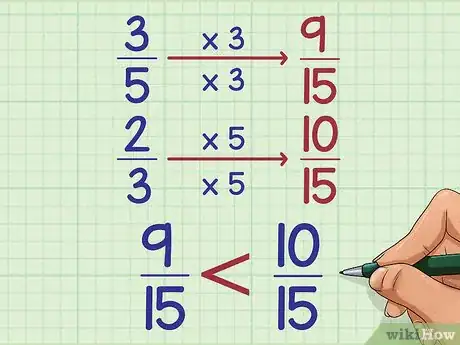
7
Comprende por qué funciona. Para comparar dos fracciones, normalmente tienes que transformarlas para que tengan el mismo denominador (la parte de abajo de una fracción). En secreto, ¡esto es lo que hace la multiplicación cruzada!^{[2]
X
Fuente de investigación} Solo se salta el paso de tener que escribir los denominadores, ya que cuando las dos fracciones tengan el mismo, solo tendrás que comparar los dos números de arriba. Este es nuestro ejemplo (3/5 vs 2/3) escrito sin el “atajo” de la multiplicación cruzada:
- 3/5=(3x3)/(5x3)=9/15
- 2/3=(2x5)/(3x5)=10/15
- 9/15 es menor que 10/15
- Por lo tanto, 3/5 es menor que 2/3
Anuncio

Método 3

Método 3 de 3:
Ordenar las fracciones mayores a uno

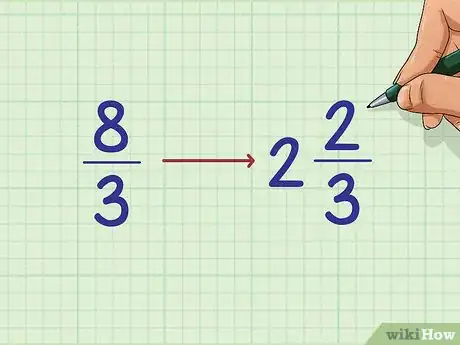
1
Emplea este método para aquellas fracciones cuyos números de arriba sean iguales o mayores a los números de abajo. Si una fracción tiene un número de arriba, o numerador, mayor que el número de abajo, o denominador, será mayor a uno. 8/3 es un ejemplo de este tipo de fracción. Puedes también emplear este método para aquellas fracciones cuyos numeradores y denominadores sean iguales, tales como 9/9. Estos dos tipos de fracciones son ejemplos de fracciones impropias.^{[3]
X
Fuente de investigación}
- Aun así puedes usar los demás métodos para estas fracciones, pero este método te ayudará a que esas fracciones tengan sentido y podrías hacerlas más rápidamente.
2
Convierte cada fracción impropia en un número mixto. Conviértelas en una mezcla de números enteros y fracciones. En ocasiones, puedes hacerlo mentalmente, por ejemplo, 9/9 = 1. Sin embargo, otras veces hay que hacer divisiones largas para averiguar cuántas veces el numerador va de manera uniforme con el denominador. El resto de ese problema largo de división, en el caso de que lo haya, se “quedará” como fracción, por ejemplo:
- 8/3 = 2 + 2/3
- 9/9 = 1
- 19/4 = 4 + 3/4
- 13/6 = 2 + 1/6
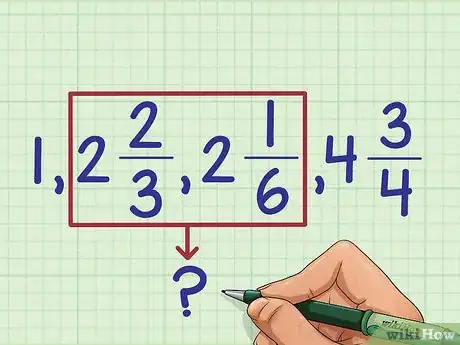
3
Ordena los números mixtos por números enteros. Ahora que ya no tienes fracciones impropias, tendrás una mejor idea del tamaño de cada número. Ignora las fracciones por el momento y clasifica las fracciones en grupos de números enteros.
- 1 es el menor
- 2 + 2/3 y 2 + 1/6 (todavía no sabemos cuál es mayor)
- 4 + 3/4 es el mayor
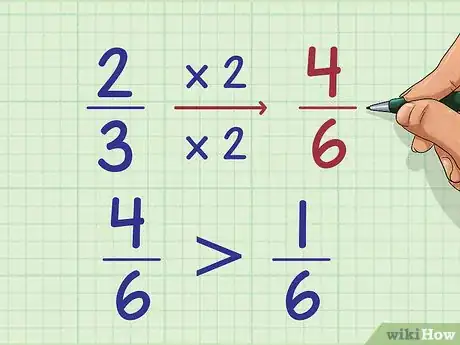
4
De ser necesario, compara las fracciones de cada grupo. Si tienes varios números mixtos con el mismo número entero, tales como 2 + 2/3 y 2 + 1/6, compara la parte de la fracción del número para ver cuál es mayor. Puedes usar cualquier de los métodos que hemos mencionado en las demás secciones para hacerlo. A continuación te presentaremos un ejemplo en el que se compara 2 + 2/3 y 2 + 1/6 donde se convierten las fracciones al mismo denominador:
- 2/3 = (2x2)/(3x2) = 4/6
- 1/6 = 1/6
- 4/6 es mayor a 1/6
- 2 + 4/6 es mayor a 2 + 1/6
- 2 + 2/3 es mayor a 2 + 1/6
5
Usa los resultados para ordenar toda la lista de números mixtos. Cuando hayas clasificado las fracciones en cada grupo de números mixtos, podrás ordenar toda la lista: 1, 2 + 1/6, 2 + 2/3, 4 + 3/4.
6
Convierte los números mixtos nuevamente a sus fracciones originales. Mantén el mismo orden, pero deshaz los cambios que hayas hecho y escribe las fracciones impropias originales: 9/9, 8/3, 13/6, 19/4.

Anuncio

Consejos

Al ordenar una gran cantidad de fracciones, puede serte de utilidad si comparas y ordenas grupos más pequeños de 2, 3 o 4 fracciones a la vez.
Si bien averiguar el mínimo común denominador es útil para que puedas trabajar con números más pequeños, cualquier denominador común servirá. Trata de ordenar 2/3, 5/6 y 1/3 con un común denominador de 36 y observa si obtienes el mismo resultado.
Si todos los numeradores son los mismos, puedes ordenarlos en el orden reverso del denominador, por ejemplo: 1/8 < 1/7 < 1/6 < 1/5. Imagina que es una pizza: si vas de 1/2 a 1/8, estarás cortando la pizza en 8 porciones y no en 2, así que tu porción será mucho más pequeña.

Anuncio