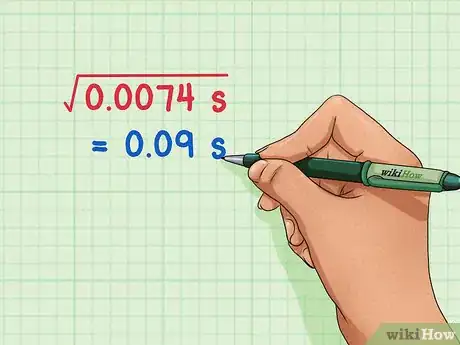Cómo calcular la incertidumbre

Información del autor

Cada vez que haces una medición mientras recolectas datos, puedes asumir que hay un "valor verdadero" que se encuentra dentro del rango de las mediciones que hiciste. Para calcular la incertidumbre de tus mediciones, debes hallar el mejor estimado de tu medición y considerar los resultados cuando sumes o restes la medición de incertidumbre. Si quieres saber cómo calcular la incertidumbre, solo sigue los siguientes pasos.

Método 1

Método 1 de 3:
Aprender los conceptos básicos

1
Enuncia la incertidumbre en su forma correcta. Digamos que vas a medir un palo cuya longitud es de aproximadamente 4,2 cm, un milímetro más o un milímetro menos. Esto significa que sabes que el palo tiene casi 4,2 cm, pero que en realidad podría ser solo un poco más pequeño o grande que esa medición, con el margen de error de un milímetro.
- Enuncia la incertidumbre de esta forma: 4,2 cm ± 0,1 cm. También puedes reescribirlo como 4,2 cm ± 1 mm, ya que 0,1 cm = 1 mm.
2
Siempre redondea la medición experimental a la misma cifra decimal que la incertidumbre. Las mediciones donde hay un cálculo de incertidumbre generalmente se redondean a una o dos cifras significativas. El punto más importante es que debes redondear tu medición experimental al mismo decimal que la incertidumbre para que tus mediciones sigan siendo coherentes.
- Si tu medición experimental es 60 cm, entonces el cálculo de la incertidumbre también debe redondearse a un número entero. Por ejemplo, la incertidumbre para esta medición puede ser 60 cm ± 2 cm, pero no 60 cm ± 2,2 cm.
- Si tu medición experimental es 3,4 cm, entonces el cálculo de la incertidumbre debe redondearse a 0,1 cm. Por ejemplo, la incertidumbre para esta medición puede ser 3,4 cm ± 0,1 cm, pero no 3,4 cm ± 1 cm.
3
Calcula la incertidumbre de una sola medición. Digamos que vas a medir el diámetro de una pelota redonda con una regla. Esto es complicado, porque será difícil determinar exactamente en qué parte los bordes externos de la pelota se alinean con la regla, ya que son curvos en lugar de rectos. Digamos que la regla puede medir a la décima de centímetro más cercana, aunque esto no significa que puedes medir el diámetro a este nivel de precisión.^{[1]
X
Fuente de investigación}
- Estudia los bordes de la pelota y la regla para obtener una idea de qué tan fiable puede ser la medición de su diámetro. En una regla estándar, las marcas a 0,5 cm aparecen claramente, pero digamos que puedes acercarte un poco más que eso. Si parece que puedes llegar a 0,3 cm de una medición precisa, entonces la incertidumbre es de 0,3 cm.
- Ahora, mide el diámetro de la pelota. Digamos que obtienes alrededor de 7,6 cm. Solo enuncia la medición estimada junto con la incertidumbre. El diámetro de la pelota es 7,6 cm ± 0,3 cm.
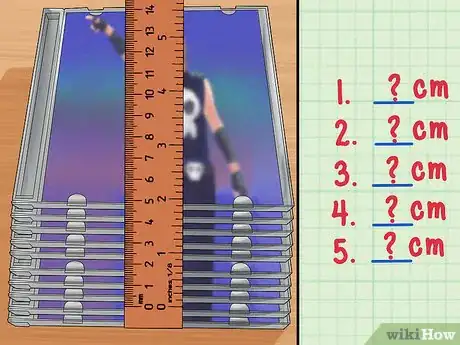
4
Calcula la incertidumbre de una sola medición de múltiples objetos. Digamos que vas a medir una pila de 10 cajas de CD que tienen la misma longitud. Digamos que quieres hallar cuánto mide el grosor de una sola caja de CD. Esta medición será tan pequeña que el porcentaje de incertidumbre será un poco alto. Pero, al medir 10 cajas de CD apiladas, puedes simplemente dividir el resultado y su incertidumbre entre el número de cajas de CD para hallar el grosor de una caja.^{[2]
X
Fuente de investigación}
- Digamos que no puedes acercarte a más de 0,2 cm de la medición usando una regla. Entonces, tu incertidumbre es ± 0,2 cm.
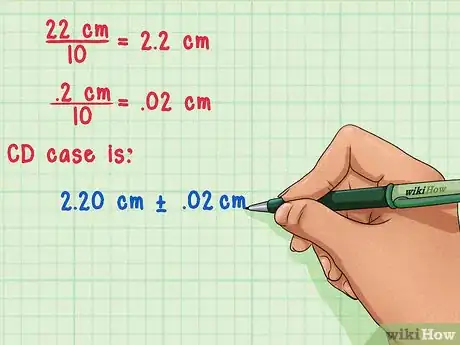
- Digamos que mediste que todas las cajas de CD apiladas tienen un grosor de 22 cm.
- Ahora, solo divide la medición e incertidumbre entre 10, el número de cajas de CD. 22 cm/10 = 2,2 cm y 0,2 cm/10 = 0,02 cm. Esto significa que el grosor de una caja de CD es 2,20 cm ± 0,02 cm.
5
Toma las mediciones muchas veces. Si quieres incrementar la certidumbre de tus mediciones, ya sea que vayas a medir la longitud de un objeto o la cantidad de tiempo que le toma a un objeto cruzar cierta distancia, toma varias mediciones para así aumentar tus posibilidades de obtener una medida precisa. Sacar el promedio de tus múltiples mediciones te ayudará a obtener una imagen más precisa de la medición mientras calculas la incertidumbre.

Anuncio

Método 2

Método 2 de 3:
Calcular la incertidumbre de múltiples mediciones

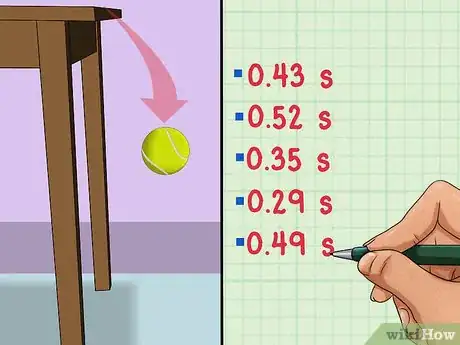
1
Toma varias mediciones. Digamos que quieres calcular cuánto tiempo le toma a una pelota caer al suelo desde la altura de una mesa. Para obtener los mejores resultados, tienes que medir la pelota cayéndose de la mesa por lo menos unas cuantas veces, digamos cinco. Luego, tienes que sacar el promedio de las cinco mediciones y sumarle o restarle a ese número la desviación estándar para obtener los mejores resultados.^{[3]
X
Fuente de investigación}
- Digamos que mediste los cinco siguientes tiempos: 0,43 s, 0,52 s, 0,35 s, 0,29 s y 0,49 s.
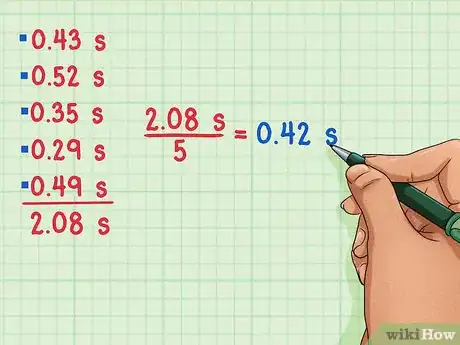
2
Saca el promedio de las mediciones. Ahora, saca el promedio sumando las cinco mediciones diferentes y dividiendo el resultado entre 5, la cantidad de mediciones. 0,43 s + 0,52 s + 0,35 s + 0,29 s + 0,49 s = 2,08 s. Ahora, divide 2,08 entre 5. 2,08/5 = 0,42 s. El tiempo promedio es 0,42 s.
3
Calcula la varianza de estas mediciones. Primero, deberás hallar la diferencia entre cada una de las cinco mediciones y el promedio. Para hacerlo, solo resta la medición a 0,42. Estas son las cinco diferencias:^{[4]
X
Fuente de investigación}
- 0,43 s – 0,42 s = 0,01 s
  - 0,52 s – 0,42 s = 0,1 s
  - 0,35 s – 0,42 s = -0,07 s
  - 0,29 s – 0,42 s = -0,13 s
  - 0,49 s – 0,42 s = 0,07 s
  - Ahora, suma los cuadrados de las siguientes diferencias: (0,01 s)² + (0,1 s)² + (-0,07 s)² + (-0,13 s)² + (0,07 s)² = 0,037 s.
  - Saca el promedio de la suma de estos cuadrados dividiendo el resultado entre 5. 0,037 s/5 = 0,0074 s.
4
Halla la desviación estándar. Para hallar la desviación típica, simplemente halla la raíz cuadrada de la varianza. La raíz cuadrada de 0,0074 s = 0,09 s, así que la desviación estándar es 0,09 s.^{[5]
X
Fuente de investigación}
5
Enuncia la medición final. Para hacerlo, simplemente enuncia el promedio de las mediciones junto con la desviación estándar que has sumado y restado. Debido a que el promedio de las mediciones es 0,43 s y la desviación estándar es 0,09 s, la medición final es 0,42 s ± 0,09 s.

Anuncio

Método 3

Método 3 de 3:
Realizar operaciones aritméticas con mediciones inciertas

1
Suma mediciones inciertas. Para sumar mediciones inciertas, simplemente suma las mediciones y suma sus incertidumbres:^{[6]
X
Fuente de investigación}
- (5 cm ± 0,2 cm) + (3 cm ± 0,1 cm) =
- (5 cm + 3 cm) ± (0,2 cm + 0,1 cm) =
- 8 cm ± 0,3 cm
2
Restar mediciones inciertas. Para restar mediciones inciertas, simplemente resta las mediciones, pero suma sus incertidumbres:^{[7]
X
Fuente de investigación}
- (10 cm ± 0,4 cm) - (3 cm ± 0,2 cm) =
- (10 cm - 3 cm) ± (0,4 cm + 0,2 cm) =
- 7 cm ± 0,6 cm
3
Multiplica mediciones inciertas.
Para multiplicar mediciones inciertas, simplemente multiplica las mediciones, pero suma sus incertidumbres RELATIVAS (como un porcentaje):^{[8]
X
Fuente de investigación} calcular la incertidumbre en una multiplicación no funciona con valores absolutos (como los que teníamos en la suma y la resta), sino con valores relativos. La incertidumbre relativa se obtiene dividiendo la incertidumbre absoluta entre un valor medido y multiplicando por 100 para obtener un porcentaje. Por ejemplo:
- (6 cm ± 0,2 cm) = (0,2 / 6) x 100 y agrega un signo de %. Esto es 3,3 %.
  Por lo tanto:
- (6 cm ± 0,2 cm) x (4 cm ± 0,3 cm) = (6 cm ± 3,3 %) x (4 cm ± 7,5 %)
- (6 cm x 4 cm) ± (3,3 + 7,5) =
- 24 cm ± 10,8 % = 24 cm ± 2,6 cm
4
Divide mediciones inciertas.
Para dividir mediciones inciertas, simplemente divide las mediciones, pero suma sus incertidumbres RELATIVAS:^{[9]
X
Fuente de investigación}¡el proceso es el mismo que para la multiplicación!
- (10 cm ± 0,6 cm) ÷ (5 cm ± 0,2 cm) = (10 cm ± 6 %) ÷ (5 cm ± 4 %)
- (10 cm ÷ 5 cm) ± (6 % + 4 %) =
- 2 cm ± 10% = 2 cm ± 0,2 cm
5
Incrementa exponencialmente una medición incierta. Para incrementar exponencialmente una medición incierta, simplemente eleva la medición a la potencia designada y luego multiplica la incertidumbre por esa potencia:^{[10]
X
Fuente de investigación}
- (2,0 cm ± 1,0 cm)³ =
- (2,0 cm)³ ± (1,0 cm) x 3 =
- 8,0 cm ± 3 cm³ ± 150 % o 8,0 cm³ ±12 cm³
Anuncio

Consejos

Puedes expresar los resultados y la incertidumbre estándar para todos los resultados en conjunto o para cada resultado dentro de un conjunto de datos. Como regla general, los datos que se obtienen de múltiples mediciones son más inciertos que los datos obtenidos directamente de mediciones individuales.

Anuncio

Advertencias

La buena ciencia nunca discute "hechos" o "verdades". Si bien es muy probable que la medición precisa se encuentre dentro de tu rango de incertidumbre, no hay una garantía de que esto sea así. La medición científica acepta inherentemente la posibilidad de equivocarse.
La incertidumbre que hemos descrito en el presente artículo solo es aplicable a casos con distribución normal (gaussiana o de forma acampanada). Otras distribuciones requieren un medio diferente para describir incertidumbres.

Anuncio