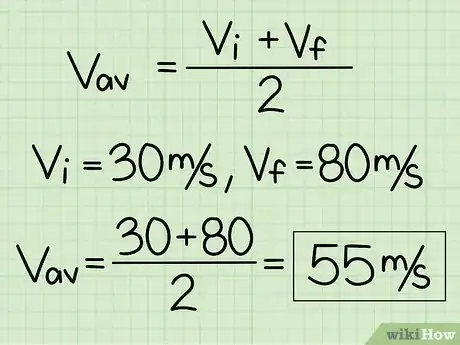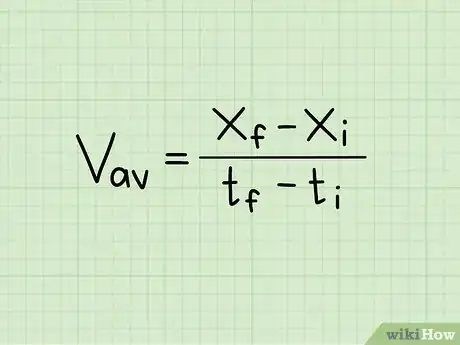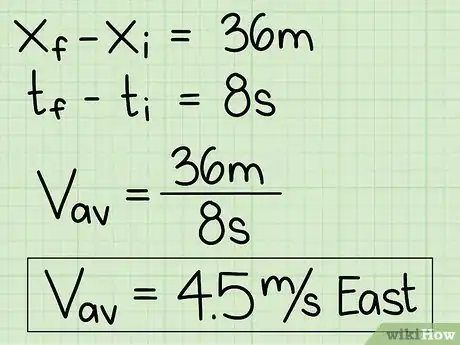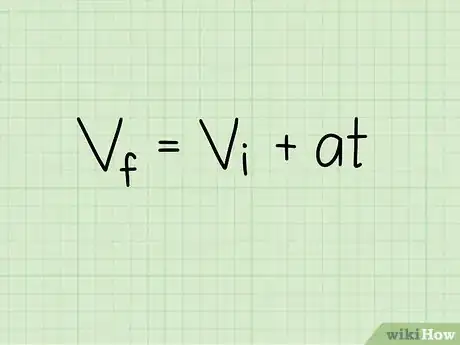Cómo calcular la velocidad

Coescrito por Sean Alexander, MS

La velocidad es la rapidez en la que viaja un objeto en una dirección en específico. Matemáticamente, la velocidad se describe como el cambio de posición de un objeto en determinado tiempo. Este concepto fundamental aparece en muchos problemas básicos de física. La fórmula que debas usar dependerá de lo que sepas sobre el objeto, así que presta mucha atención al problema para así usar la fórmula correcta.

Fórmulas rápidas

Velocidad promedio = $v_{av}={\frac {x_{f}-x_{i}}{t_{f}-t_{i}}}$ $v_{{av}}={\frac {x_{f}-x_{i}}{t_{f}-t_{i}}}$
- $x_{f}=$ posición final $x_{i}=$ posición inicial
- $t_{f}=$ tiempo final $t_{i}=$ tiempo inicial
Velocidad promedio si la aceleración es constante = $v_{av}={\frac {v_{i}+v_{f}}{2}}$ $v_{{av}}={\frac {v_{i}+v_{f}}{2}}$
- $v_{i}=$ velocidad inicial $v_{f}=$ velocidad final
Velocidad promedio si la aceleración es de cero y constante = $v_{av}={\frac {x}{t}}$
Velocidad final = $v_{f}=v_{i}+at$ $v_{f}=v_{i}+at$
- a = aceleración t = tiempo

Método 1

Método 1 de 3:
Encontrar la velocidad promedio

1
Encuentra la velocidad promedio cuando la aceleración es constante. Si el objeto acelera a un ritmo constante, la fórmula de la velocidad promedio es muy simple: $v_{av}={\frac {v_{i}+v_{f}}{2}}$ $v_{{av}}={\frac {v_{i}+v_{f}}{2}}$ . En esta ecuación $v_{i}$ $v_{i}$ es la velocidad inicial y $v_{f}$ $v_{f}$ es la velocidad final. Recuerda que solo puedes usar esta ecuación si no hay ningún cambio en la aceleración.
- Por ejemplo, supongamos que un tren acelera a un ritmo constante de 30 m/s a 80 m/s. La velocidad promedio del tren durante este tiempo es de ${\frac {30+80}{2}}=55m/s$ .
2
Configura ahora una ecuación usando la posición y el tiempo. También puedes encontrar la velocidad usando el cambio en la posición y el tiempo del objeto. Esto funciona para cualquier problema. Ten en mente que a menos que el objeto se esté moviendo en una velocidad constante, la respuesta será la velocidad promedio durante el movimiento, no la velocidad actual en cierto periodo de tiempo.
- La fórmula para este problema es $v_{av}={\frac {x_{f}-x_{i}}{t_{f}-t_{i}}}$ o "posición final – posición inicial dividida entre el tiempo final – tiempo inicial". También puedes escribir la fórmula de la siguiente manera $v_{av}$ = ^Δx / _Δt o "el cambio en la posición sobre el cambio en tiempo."
3
Encuentra la distancia entre el punto inicial y el punto final. Al medir la velocidad, las únicas posiciones que importan son la posición donde empezó el objeto y dónde termine el objeto. Esto, junto con la dirección en la que viajó el objeto, te indica el desplazamiento o el cambio en posición.^{[1]
X
Fuente de investigación} El camino que tomó el objeto entre estos dos puntos no importa.
- Ejemplo 1: un carro que viaja hacia el este comienza en la posición x = 5 metros. Al pasar 8 segundos, el carro está en la posición x = 41 metros. ¿Cuál es el desplazamiento del carro?
  - El carro se desplazó (41m - 5m) = 36 metros al este.
- Ejemplo 2: un clavadista salta 1 metro recto hacia arriba desde un trampolín y después cae 5 metros antes de tocar el agua. ¿Cuál fue el desplazamiento del clavadista?
  - El clavadista termino 4 metros debajo del punto inicial, así que el desplazamiento es 4 metros hacia abajo o -4 metros. (0 + 1 - 5 = -4). Aunque el clavadista viajo 6 metros (uno hacia arriba y cinco hacia abajo), lo que importa es que el punto final está 4 metros debajo del punto inicial.
4
Calcula el cambio en tiempo. ¿Cuánto tardo el objeto en llegar al punto final? Muchos problemas te informarán de esto directamente. Si el problema no lo hace, resta el tiempo inicial del tiempo final para averiguarlo.
- Ejemplo 1 (continuación): el problema nos dice que al carro le tomó 8 segundos llegar del punto inicial al punto final, así que ese es el cambio en tiempo.
- Ejemplo 2 (continuación): si el clavadista brincó a los t = 7 segundos y tocó el agua a los t = 8 segundos, el cambio en tiempo es de = 8s - 7s = 1 segundo.
5
Divide el desplazamiento total entre el tiempo total. Para poder encontrar la velocidad del objeto en movimiento, necesitas dividir el cambio en la posición entre el cambio en el tiempo. Especifica la dirección en la que se movió el objeto y tendrás la velocidad promedio.
- Ejemplo 1 (continuación): el carro cambió de posición, viajó 36 metros en 8 segundos. $v_{av}={\frac {36m}{8s}}=$ 4.5 m/s al este.
- Ejemplo 2 (continuación): el clavadista cambió su posición, -4 metros en 1 segundo. $v_{av}={\frac {-4m}{1s}}=$ -4 m/s. (En una dimensión, los números negativos se usan para significar "hacia abajo" o "hacia la izquierda". Así que también se puede decir "4 m/s hacia abajo").
6
Resuelve problemas en dos dimensiones. No todos los problemas involucran un movimiento en solo una línea. Si el objeto gira hacia otro lado en algún momento, necesitas dibujar el diagrama y resolver el problema geométrico para encontrar la distancia.
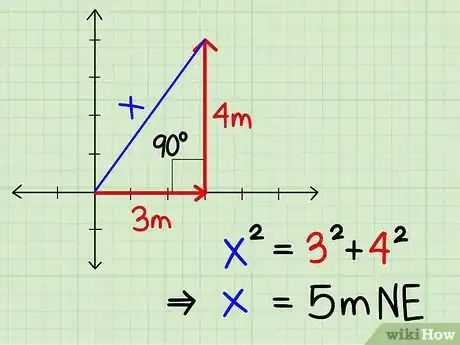
- Ejemplo 3: un hombre trota 3 metros hacia el este, después hace un giro de 90 grados y sigue trotando 4 metros hacia el norte. ¿Cuál fue su desplazamiento?
  - Dibuja un diagrama y conecta el punto inicial con el punto final en una línea recta. Esta es la hipotenusa del triángulo, así que tienes que averiguar el largo de esta línea usando las propiedades de los triángulos rectos. En este caso, el desplazamiento es de 5 metros al noreste.
  - En algún punto, tu maestro de matemáticas te pedirá que encuentres la dirección exacta en la que viajó el objeto (el ángulo sobre la línea horizontal). Puedes hacer esto usando fórmulas de geometría o sumando los vectores.^{[2]
    X
    Fuente de investigación}

Método 2

Método 2 de 3:
Encontrar la velocidad usando la aceleración

1
Comprende la fórmula de la velocidad para un objeto que está acelerando. La aceleración es el cambio en la velocidad. Si la aceleración es constante, la velocidad continúa cambiando al mismo ritmo. Podemos describir esto multiplicando la aceleración y el tiempo y sumando el resultado a la velocidad inicial:
- $v_{f}=v_{i}+at$ o "velocidad final = velocidad inicial + (aceleración * tiempo)"
- La velocidad inicial $v_{i}$ a veces se escribe de la siguiente manera $v_{0}$ ("velocidad al momento de 0").
2
Multiplica la aceleración por el cambio en el tiempo. Esto te dirá cuánto ha incrementado la velocidad (o disminuido) en dicho periodo de tiempo.
- Ejemplo: un barco que se dirige hacia el norte a 2 m/s acelera hacia el norte a un ritmo de 10 m/s². ¿Cuánto incremento la velocidad del barco en los siguientes 5 segundos?
  - a = 10 m/s²
  - t = 5 s
  - (a * t) = (10 m/s² * 5 s) = 50 m/s incremento en velocidad.
3
Añade la velocidad inicial. Ahora que sabes el cambio total en la velocidad. Suma esto a la velocidad inicial del objeto y tendrás tu respuesta.
- Ejemplo (continuación): en este ejemplo, ¿qué tan rápido viaja el barco después de 5 segundos?
  - $v_{f}=v_{i}+at$
  - $v_{i}=2m/s$
  - $at=50m/s$
  - $v_{f}=2m/s+50m/s=52m/s$
4
Especifica la dirección del movimiento. A diferencia de la rapidez, la velocidad siempre incluye la dirección del movimiento. Asegúrate de incluir esto en tu respuesta.
- En el ejemplo anterior, debido a que el barco siguió viajando hacia el norte y no cambió de dirección, la velocidad final es 52 m/s norte.
5
Resuelve problemas relacionados. Siempre y cuando sepas la aceleración y la velocidad en un punto de tiempo, puedes usar esta fórmula para encontrar la velocidad en cualquier otro punto de tiempo. A continuación hay un ejemplo para encontrar la velocidad inicial:
- "Un tren acelera a 7 m/s² durante 4 segundos y termina viajando a una velocidad de 35 m/s. ¿Cuál era su velocidad inicial?"
  - $v_{f}=v_{i}+at$
    $35m/s=v_{i}+(7m/s^{2})(4s)$
    $35m/s=v_{i}+28m/s$
    $v_{i}=35m/s-28m/s=7m/s$

Método 3

Método 3 de 3:
Velocidad circular

1
Aprende la fórmula para la velocidad circular. La velocidad circular se refiere a la velocidad que un objeto debe viajar para poder mantener su órbita alrededor de otro objeto, por lo general un planeta o cualquier otra masa gravitante.^{[3]
X
Fuente de investigación}
- La velocidad circular de un objeto se calcula dividiendo la circunferencia de un camino circular entre el periodo de tiempo en el que el objeto tarda en viajar dicho camino.
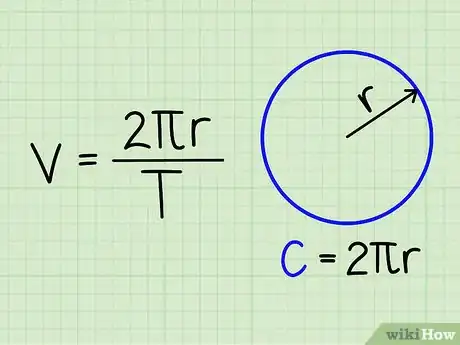
- Al escribir esta información en fórmula, la ecuación es la siguiente:
  - v = ^(2πr) / _T
- Ten en mente que 2πr es igual a la circunferencia de camino circular.
- r es "radio"
- T es el "periodo de tiempo"
2
Multiplica el radio circular por 2π. La primera etapa del problema es calcular la circunferencia. Para hacer esto, multiplica el radio por 2π. Si quieres calcular esto a mano, puedes usar 3,14 como una aproximación para π.
- Ejemplo: encuentra la velocidad circular de un objeto que viaja en un camino circular con un radio de 8 metros en un intervalo de tiempo completo de 45 segundos.
  - r = 8 m
  - T = 45 s
  - Circunferencia: 2πr = ~ (2)(3,14)(8 m) = 50,24 m
3
Divide este producto entre el periodo de tiempo. Para poder encontrar la velocidad circular del objeto en cuestión, necesitas dividir la circunferencia que calculaste entre el periodo de tiempo en el que viajó el objeto.
- Ejemplo: v = ^(2πr) / _T = ^{50,24 m} / _{45 s} = 1,12 m/s
  - La velocidad circular del objeto es 1,12 m/s.

Consejos

Metros por segundo (m/s) es la unidad científica estándar para la velocidad. Asegúrate de que las unidades coincidan midiendo la distancia en metros (m), el tiempo en segundos (s) y la aceleración en metros por segundo al cuadrado (m/s²).
La velocidad promedio mide la velocidad de un objeto a lo largo de todo un trayecto. La velocidad instantánea mide la velocidad de un objeto en un momento específico a lo largo de un trayecto.