Nuestro equipo de editores e investigadores capacitados han sido autores de este artículo y lo han validado por su precisión y amplitud.
wikiHow's Content Management Team revisa cuidadosamente el trabajo de nuestro personal editorial para asegurar que cada artículo cumpla con nuestros altos estándares de calidad.
Este artículo ha sido visto 309 391 veces.
Para calcular la velocidad media, todo lo que necesitas es el desplazamiento total o el cambio en posición, además del tiempo total. Recuerda que la velocidad mide la dirección y la rapidez, así que incluye la dirección en tu respuesta, como por ejemplo “norte”, “adelante” o “izquierda”. Si el problema implica la aceleración constante, puedes aprender un atajo que te ayudará a encontrar una solución aún más sencilla.
Pasos
Parte 1
Parte 1 de 2:Calcular la velocidad media con el desplazamiento y el tiempo
-
1Recuerda que la velocidad incluye la rapidez y la dirección. La velocidad describe el índice en el cual un objeto cambia de posición. Esto está relacionado a la rapidez en la que viaja el objeto, pero también a la dirección. “100 metros por segundo al sur” es una velocidad distinta que "100 metros por segundo al este”.
- Las cantidades que incluyen una dirección se llaman cantidades vectoriales'.[1] Pueden distinguirse de las cantidades sin dirección o escalares al escribir una flecha sobre la variable. Por ejemplo, v representa a la rapidez mientras que v→ representa a la velocidad o a la rapidez + la dirección.[2] Si en este artículo se utiliza una v, significa que se hace referencia a la velocidad.
- En problemas científicos, debes utilizar metros u otra unidad métrica de distancia, pero en la vida diaria puedes utilizar cualquier unidad con la que te sientas cómodo.
-
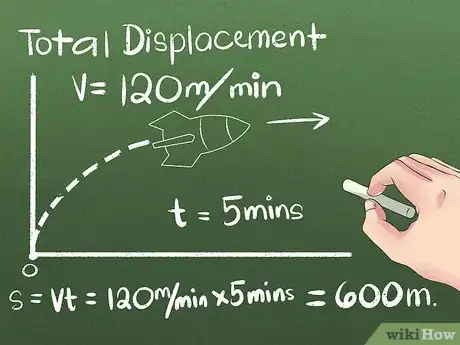
2Halla el desplazamiento total. El desplazamiento es el cambio del objeto en posición o la distancia y la dirección entre su punto de partida y el de llegada. No importa hacia dónde se haya movido el objeto antes de alcanzar su posición final; lo único que interesa es la distancia entre el punto de partida y el de llegada. Para nuestro primer ejemplo, utilizaremos un objeto que se mueve a una rapidez constante en una dirección:
- Supongamos que un cohete viajó hacia el norte durante 5 minutos a una velocidad constante de 120 metros por minuto. Para calcular su posición final, utiliza la fórmula s = vt o utiliza el sentido común para averiguar que el cohete debe estar a (5 minutos)(120 metros por minuto) = 600 metros al norte de su punto de partida.
- Para los problemas que involucren una aceleración constante, puedes resolver s = vt + ½at2 o revisar la siguiente sección para ver un método más corto que te permita hallar la respuesta.
-
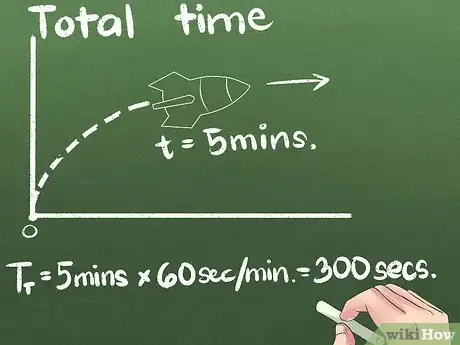
3Halla la cantidad total del tiempo transcurrido. En nuestro ejemplo, el cohete avanzó durante 5 minutos. Puedes expresar la velocidad media en cualquier unidad de tiempo, pero los segundos son la norma científica internacional. En este ejemplo, convertiremos a segundos: (5 minutos) x (60 segundos por minuto) = 300 segundos .
- Incluso en un problema científico, si el problema emplea unidades de horas o periodos de tiempo más largos, puede ser más fácil calcular la velocidad y luego convertir la respuesta final a metros por segundo (m/s).
-
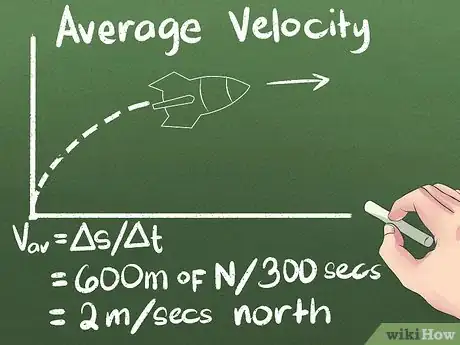
4Calcula la velocidad media como el desplazamiento a lo largo del tiempo. Si sabes qué tan lejos viajó un objeto y cuánto tiempo le tomó llegar hasta ahí, sabes lo rápido que iba. De modo que en nuestro ejemplo, la velocidad media del cohete era (600 metros hacia el norte) / (300 segundos) = 2 metros por segundos hacia el norte.
- Recuerda incluir la dirección (como, por ejemplo, hacia “adelante” o hacia el “norte”).
- Utiliza la fórmula vav = Δs/Δt. El símbolo delta (Δ) simplemente significa “cambio”, de modo que Δs/Δt significa “cambio en la posición a lo largo del cambio en el tiempo”.
- La velocidad media puede escribirse como vav o como una v con una línea horizontal sobre ella.
-
5Resuelve problemas más complejos. Si un objeto gira o cambia de velocidad, no te confundas. La velocidad media se calcula solo a partir del desplazamiento y del tiempo total. No interesa lo que ocurra entre el punto de partida. Estos son algunos ejemplos de trayectos con el mismo desplazamiento y tiempo exacto, y por lo tanto la misma velocidad media:
- Ana camina hacia el oeste a 1 m/s durante dos segundos, luego acelera instantáneamente a 3 m/s y sigue caminando hacia el oeste durante 2 segundos. Su desplazamiento total es: (1 m/s oeste)(2 s) + (3 m/s oeste)(2 s) = 8 metros hacia el oeste. Su tiempo total es 2s + 2s = 4s. Su velocidad media es 8 m oeste / 4s = 2 m/s oeste.
- Bernardo camina hacia el oeste a 5 m/s durante 3 segundos, luego da la vuelta y camina hacia el este a 7 m/s durante 1 segundo. Podemos tratar el movimiento hacia el este como “un movimiento negativo hacia el este”, de modo que el desplazamiento total = (5 m/s oeste)(3 s) + (-7 m/s oeste)(1 s) = 8 metros. Tiempo total = 4s. Velocidad media = 8 m oeste / 4s = 2 m/s oeste.
- Carlota camina 1 metro hacia el norte, luego 8 metros hacia el oeste y por último 1 metro hacia el sur. Le toma 4 segundos en total recorrer esta distancia. Dibuja un diagrama en una hoja de papel y verás que recorre 8 metros hacia el oeste desde su punto de partida, de modo que este es su desplazamiento. Una vez más, el tiempo total es de 4 segundos, así que la velocidad media sigue siendo de 8 m oeste / 4s = 2 m/s oeste.
Anuncio
Parte 2
Parte 2 de 2:Calcular la velocidad media a partir de la aceleración constante
-
1Ten en cuenta la velocidad inicial y la aceleración constante. Supongamos que tu problema es “La motocicleta comienza a viajar hacia la derecha a unos 5 m/s acelerando constantemente unos 2 m/s2. Si viaja durante 5 segundos, ¿cuál es su velocidad media?”.
- Si la unidad “m/s2” no tiene sentido para ti, escríbela como “m/s/s” o “metros por segundo por segundo”.[3] Una aceleración de 2 m/s/s significa que la velocidad aumenta en 2 metros por segundo a cada segundo.
-
2Emplea la aceleración para hallar la velocidad final. La aceleración (descrita como a) es el índice del cambio en la velocidad (o en la rapidez). La velocidad se eleva a un ritmo constante. Puedes dibujar una gráfica utilizando la aceleración para hallar la velocidad en diferentes momentos durante esta trayectoria. Necesitaremos hacerlo para hallar el momento final en el problema (en t = 5 segundos), pero escribiremos una gráfica más larga para ayudarte a entender este concepto:
- Al principio (tiempo t = 0 segundos), la motocicleta viaja hacia la derecha a 5 m/s.
- Después de 1 segundo (t = 1), la motocicleta se mueve a 5 m/s + at = 5 m/s + (2 m/s2)(1 s) = 7 m/s.
- En t = 2, la motocicleta se mueve hacia la derecha a 5+(2)(2) = 9 m/s.
- En t = 3, la motocicleta se mueve hacia la derecha a 5+(2)(3) = 11 m/s.
- En t = 4, la motocicleta se mueve hacia la derecha a 5+(2)(4) = 13 m/s.
- En t = 5, la motocicleta se mueve hacia la derecha a 5+(2)(5) = 15 m/s.
-
3Utiliza esta fórmula para hallar la velocidad media. Si y solo si la aceleración es constante, la velocidad media es la misma que la media de la velocidad final y la velocidad inicial: (vf + vi)/2. En nuestro ejemplo, la velocidad inicial de la motocicleta vi es 5 m/s. Tal como lo resolvimos anteriormente, termina viajando a una velocidad final vf de 15 m/s. Al conectar estos números obtenemos (15 m/s + 5 m/s) / 2 = (20 m/s) / 2 = 10 m/s derecha.
- No olvides incluir la dirección, en este caso “derecha”.
- Estos términos pueden escribirse como v0 (velocidad en el tiempo 0 o velocidad inicial) y simplemente v (velocidad final).
-
4Comprende la fórmula para la velocidad media de manera intuitiva. Para hallar la velocidad media, podríamos tomar la velocidad en cada momento y hallar la media de toda la lista (esta es la definición de media). Dado que eso requeriría un cálculo o un tiempo infinito, utilicemos una explicación más intuitiva. En lugar de cada momento en el tiempo, tomemos la media de la velocidad en solo dos puntos en el tiempo y veamos lo que obtenemos. Un punto en el tiempo estará cerca del principio del trayecto, cuando la motocicleta viaje con lentitud, y el otro estará igualmente cerca del final del trayecto, cuando la motocicleta viaje con rapidez.
-
5Prueba la teoría intuitiva. Utiliza la gráfica anterior para las velocidades en puntos distintos en el tiempo. Algunos de los pares que encajan con los criterios están en (t=0, t=5), (t=1, t=4) o (t=2, t=3). Si gustas, también puedes probarlo con valores no enteros de t.
- Sin importar los pares de puntos que escojamos, la media de dos velocidades en esos tiempos siempre será la misma. Por ejemplo, ((5+15)/2), ((7+13)/2) o ((9+11)/2) son todos iguales a 10 m/s a la derecha.
-
6Termina la explicación intuitiva. Si empleáramos este método con una lista de cada momento en el tiempo (de alguna manera), seguiríamos promediando una velocidad desde la primera mitad con una velocidad de la segunda mitad del trayecto. Existe una cantidad igual de tiempo en cada mitad, así que ninguna de ellas quedaría sin explicación para cuando terminemos.
- Dado que cualquiera de estos pares se promedia con la misma cantidad, la media de todas estas velocidades será igual a dicha cantidad. En nuestro ejemplo, la media de todas esos “10 m/s a la derecha” seguirá siendo 10 m/s a la derecha.
- Podemos hallar esta cantidad al promediar cualquiera de estos pares, por ejemplo, las velocidades inicial y final. En nuestro ejemplo, estas se encuentran en t=0 y t=5, y pueden calcularse utilizando la fórmula anterior: (5+15)/2 = 10 m/s a la derecha.
-
7Entiende la fórmula de manera matemática. Si te sientes más cómodo con una prueba escrita, como las fórmulas, puedes comenzar con la fórmula para la distancia recorrida asumiendo la aceleración constante y luego deriva dicha fórmula a partir de ahí:[4]
- s = vit + ½at2 (técnicamente Δs y Δt, o el cambio en la posición y en el tiempo, pero te dejarás entender si utilizas s y t).
- La velocidad media vav se define como s/t, así que pongamos la fórmula en términos de s/t.
- vav = s/t = vi + ½at
- La aceleración por el tiempo es igual al cambio total en la velocidad o vf - vi. De modo que podemos reemplazar “at” en la fórmula y obtener:
- vav = vi + ½(vf - vi).
- Simplifica: vav = vi + ½vf - ½vi = ½vi + ½vf = (vf + vi)/2.
Anuncio
Consejos
- La velocidad es diferente a la rapidez debido a que la primera es una cantidad vectorial y la rapidez es una cantidad escalar. Las cantidades vectoriales muestran la dirección así como la magnitud mientras que las cantidades escalares únicamente muestran la magnitud.
- Si el objeto se mueve únicamente en una dimensión, como por ejemplo de izquierda a derecha, puedes utilizar números positivos para representar una dirección (por ejemplo, derecha) y los negativos para representar la otra (izquierda). Anótalo en la parte superior de la página para que quede en claro para las personas que lean tu trabajo. tambien que la rapidez indica la longitud recorrida del movil en un intervalo de tiempo
- Para hallar la velocidad de un objeto en un momento específico a lo largo de un trayecto, necesitarás calcular la velocidad instantánea en lugar de la velocidad promedio.
Referencias
- ↑ http://www.physicsclassroom.com/Class/1DKin/U1L1b.cfm
- ↑ https://www.khanacademy.org/science/physics/one-dimensional-motion/displacement-velocity-time/v/calculating-average-velocity-or-speed
- ↑ http://www.physicsclassroom.com/class/1DKin/Lesson-1/Acceleration
- ↑ http://physics.stackexchange.com/questions/44685/why-is-average-velocity-the-midpoint-of-initial-and-final-velocity-under-constan
































wikiHow's Content Management Team revisa cuidadosamente el trabajo de nuestro personal editorial para asegurar que cada artículo cumpla con nuestros altos estándares de calidad. Este artículo ha sido visto 309 391 veces.