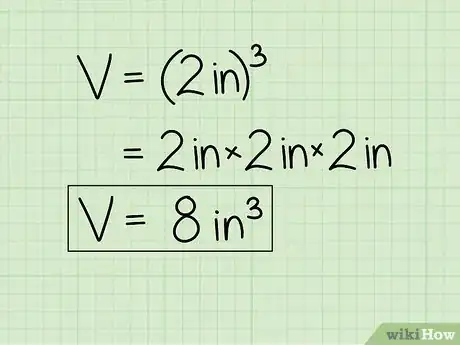wikiHow es un "wiki", lo que significa que muchos de nuestros artículos están escritos por varios autores. Para crear este artículo, 82 personas, algunas anónimas, han trabajado para editarlo y mejorarlo con el tiempo.
Este artículo ha sido visto 1 412 770 veces.
Un cubo es una figura tridimensional cuyas medidas son iguales en longitud, profundidad y altura. Un cubo está formado por seis caras cuadradas, cada una de las cuales tiene todos sus lados iguales, formando ángulos rectos entre sí. Hallar el volumen de un cubo suele ser bastante sencillo; lo único que tienes que hacer es multiplicar longitud × profundidad × altura. Dado que todas las aristas de un cubo tienen la misma longitud, otra definición de su volumen es s3, donde s es la longitud de cualquiera de sus aristas. Lee los siguientes pasos para conocer este proceso de forma detallada.
Pasos
Método 1
Método 1 de 3:Elevar al cubo una arista del cubo
-
1Halla la longitud de cualquiera de las aristas del cubo. Muchas veces, en los problemas que piden hallar el volumen de un cubo, se dará a conocer la longitud de una de sus aristas. Si dispones de este dato, ya tienes todo lo que necesitas para calcular el volumen. Si no se trata de un problema abstracto de matemáticas, sino más bien quieres hallar el volumen de un objeto real con forma de cubo, utiliza una regla o un metro para conocer la longitud de sus aristas.
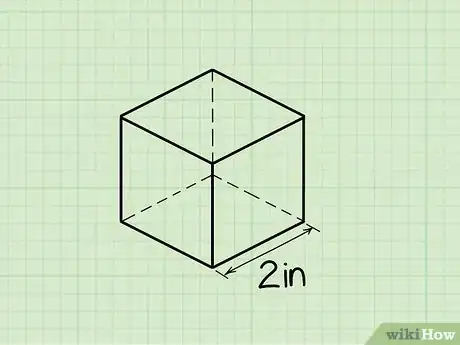
- Para entender mejor el proceso de calcular el volumen de un cubo, utilizaremos un problema como ejemplo para indicar los pasos de esta sección. Supongamos que la arista del cubo mide 5 cm (2 pulgadas) de largo. Aprovecharemos este dato para hallar el volumen del cubo en el siguiente paso.
-
2Eleva al cubo la longitud de la arista. Cuando hayas averiguado la longitud de cualquiera de las aristas del cubo, eleva esta cifra al cubo. En otras palabras, multiplícala dos veces por sí misma. Si s es la longitud de la arista, tendrás que multiplicar s × s × s (o, de forma simplificada, s3). El resultado de esta operación nos dará el volumen del cubo.
- Este proceso consiste, básicamente, en hallar el área de la base y multiplicarla por la altura (o, en otras palabras, longitud × profundidad × altura), ya que el área de la base se calcula multiplicando su longitud por su profundidad. Dado que la longitud, la profundidad y la altura de un cubo son iguales, podemos acortar el proceso elevando al cubo cualquiera de estas medidas.
- Sigamos con el ejemplo. Dado que la longitud de cualquier arista de este cubo es de 5 cm (2 pulgadas), podemos hallar el volumen multiplicando 5 x 5 x 5 (o 53) = 125.
-
3Expresa el resultado en unidades cúbicas. Dado que el volumen es la medida del espacio tridimensional, la respuesta debe expresarse en unidades cúbicas por definición. Muchas veces, los alumnos escolares se descuidan a la hora de indicar las unidades en los resultados de los problemas matemáticos, lo cual puede hacerles perder puntos; así que nunca te olvides de indicar las unidades correctamente.
- En el ejemplo, dado que la medida original se da en centímetros, la respuesta final se expresará en centímetros cúbicos (o en cm3). Por lo tanto, la respuesta de 125 se convertirá en 125 cm3.
- Si hubiésemos utilizado una unidad de medida inicial distinta, la unidad en el resultado final también sería distinta. Por ejemplo, si dijésemos que el cubo tiene aristas de 5 metros de longitud, en lugar de 5 centímetros, el resultado se expresaría en metros cúbicos (m3).
Anuncio
Método 2
Método 2 de 3:Hallar el volumen a partir del área de la superficie
-
1Halla el área de la superficie del cubo. Aunque la forma más sencilla de hallar el volumen de un cubo es elevar la longitud de cualquiera de sus aristas al cubo, este no es el único método válido. La longitud de una de las aristas del cubo o el área de cualquiera de sus caras se pueden conocer a partir de otras propiedades del cubo, lo cual significa que, si dispones de alguno de estos datos al empezar el problema, podrás calcular el volumen con un método menos directo. Por ejemplo, si conoces el área de la superficie de un cubo, lo único que tienes que hacer para hallar el volumen es dividir el área de la superficie entre 6 y, después, calcular la raíz cuadrada de este valor para conocer la longitud de una de sus aristas. A partir de este punto, el proceso consiste en elevar al cubo la longitud de la arista para calcular el volumen de la forma corriente. En esta sección, veremos el proceso paso a paso.
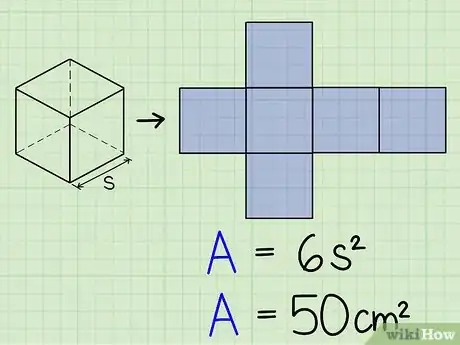
- El área de la superficie de un cubo se define por la fórmula 6s2, donde s es la longitud de cualquiera de sus aristas. Esta fórmula consiste, básicamente, en hallar el área (valor bidimensional) de cualquiera de las seis caras del cubo y sumar el área de todas sus caras. Utilizaremos esta fórmula para calcular el volumen del cubo a partir del área de su superficie.
- Como ejemplo, supongamos que tenemos un cubo cuya superficie sabemos que mide 50 cm2, pero cuya longitud de arista desconocemos. En los siguientes pasos, aprovecharemos estos datos para hallar el volumen del cubo.
-
2Divide el área de la superficie del cubo entre 6. Dado que el cubo tiene 6 caras, todas con la misma área, dividir la superficie total entre 6 nos dará como resultado el área de una de las caras. Este área es igual al resultado de multiplicar las longitudes de dos aristas (l × w, w × h, o h × l).
- Siguiendo el ejemplo, operaremos de la siguiente forma: 50/6 = 8,33 cm2. Recuerda que las respuestas con valores bidimensionales deben expresarse en unidades cuadradas (cm2, in2, m2, etc).
-
3Calcula la raíz cuadrada de este valor. Dado que el área de cualquiera de las caras del cubo es igual a s2 (s × s), calcular la raíz cuadrada de este valor te permitirá conocer la longitud de cualquiera de las aristas. Una vez que tengas este dato, podrás hallar el volumen del cubo de la forma usual.
- En el ejemplo, √8,33 = 2,89 cm.
-
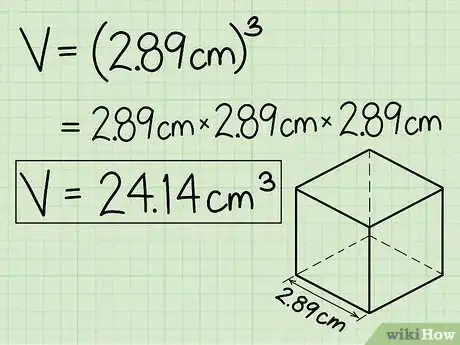
4Eleva este valor al cubo para hallar el volumen del cubo. Ahora que has obtenido la longitud de la arista del cubo, solo tendrás que elevar este valor al cubo (multiplicándolo dos veces por sí mismo) para hallar el volumen del cubo de la forma explicada en la sección anterior. Enhorabuena; ya tienes el volumen del cubo, calculado a partir del área de su superficie.
- En el ejemplo, 2,89 × 2,89 × 2,89 = 24,14 cm3. No te olvides de expresar el resultado en unidades cúbicas.
Anuncio
Método 3
Método 3 de 3:Hallar el volumen a partir de las diagonales
-
1Divide la diagonal que cruza una de las caras del cubo entre √2 para hallar la longitud de la arista del cubo. Por definición, la diagonal de un cuadrado perfecto es √2 × la longitud de una de las aristas. Por lo tanto, si el único dato que conoces del cubo está relacionado con la longitud de la diagonal de cualquiera de sus caras, podrás hallar la longitud de una arista del mismo dividiendo este valor entre √2. A partir de este punto, es relativamente fácil elevar el resultado al cubo y hallar el volumen del cubo siguiendo el método descrito arriba.
- Por ejemplo, supongamos que la diagonal de una de las caras del cubo tiene una longitud de 7 pies. Podemos hallar la longitud de una arista del cubo operando de la siguiente forma: 7/√2 = 4,96 pies. Ahora que conocemos la longitud de la arista, podremos hallar el volumen del cubo a través de la siguiente operación: 4,963 = 122,36 pies3.
- Ten en cuenta que, en términos generales, d2 = 2s2 donde d es la longitud de la diagonal de una de las caras del cubo y s es la longitud de una de las aristas del cubo. Esto se debe a que, de acuerdo con el teorema de Pitágoras, el cuadrado de la hipotenusa de un triángulo rectángulo es igual a la suma de los cuadrados de los otros dos lados. Por lo tanto, como la diagonal de la cara de un cubo y dos de los lados (aristas) de la misma cara forman un triángulo rectángulo, d2 = s2 + s2 = 2s2.
-
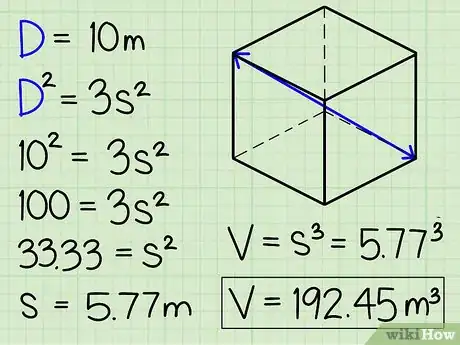
2Eleva al cuadrado la diagonal de dos esquinas opuestas del cubo y, después, divide el valor entre 3 y calcula su raíz cuadrada para hallar la longitud de la arista. Aunque el único dato dado en el problema sea la longitud de un segmento tridimensional que se extiende diagonalmente entre dos esquinas opuestas del cubo, puedes hallar el volumen de dicha figura. Dado que d es uno de los lados de un triángulo rectángulo que tiene la diagonal entre dos esquinas opuestas del cubo como hipotenusa, podemos decir que D2 = 3s2, donde D = la diagonal tridimensional que se extiende entre dos esquinas opuestas del cubo.
- Esto se debe al teorema de Pitágoras. D, d, y s forman un triángulo rectángulo, con D como hipotenusa, por lo que podemos decir que D2 = d2 + s2. Como ya habíamos calculado antes que d2 = 2s2, también podemos decir que D2 = 2s2 + s2 = 3s2.
- Por ejemplo, supongamos que sabemos que la diagonal que se extiende entre una esquina de la base del cubo y su esquina superior opuesta mide 10 m de longitud. Si queremos calcular el volumen, sustituiríamos cada "D" de la ecuación arriba mencionada por el valor numérico "10" de la siguiente forma:
- D2 = 3s2.
- 102 = 3s2.
- 100 = 3s2
- 33,33 = s2
- 5,77 m = s. A partir de este punto, lo único que tendremos que hacer para hallar el volumen del cubo es elevar al cubo la longitud de su arista.
- 5,773 = 192,45 m3
Anuncio
Acerca de este wikiHow
Para calcular el volumen de un cubo, encuentra la longitud de uno de sus lados. Una vez que tengas esta medida, multiplícala por sí misma dos veces para obtener el volumen. Esto es lo que se conoce como "elevar un número al cubo". Por ejemplo, si la longitud de los lados del cubo es igual a 2, multiplica 2 × 2 × 2 y obtendrás un volumen igual a 8. ¡Asegúrate de poner las unidades cúbicas en la respuesta!