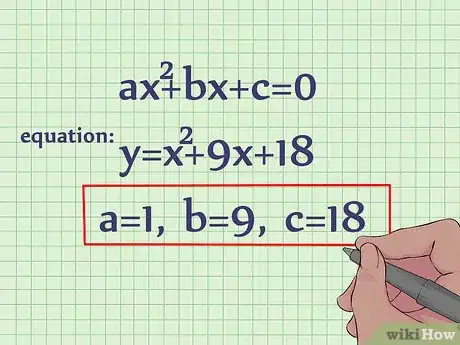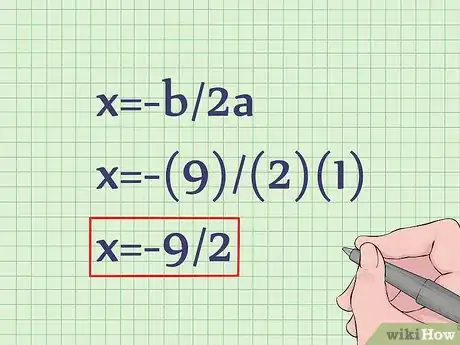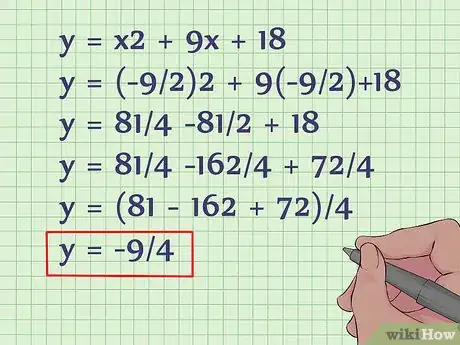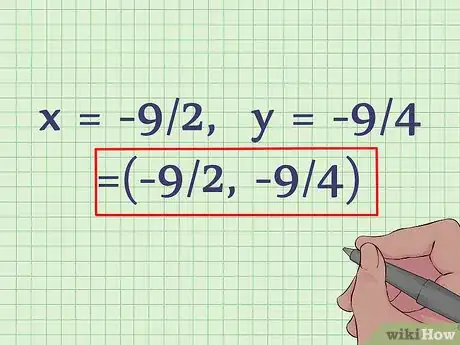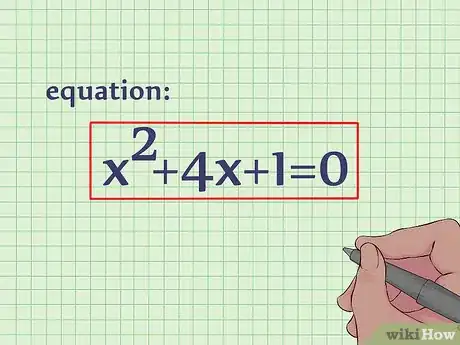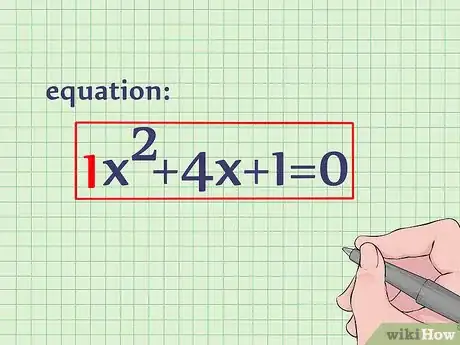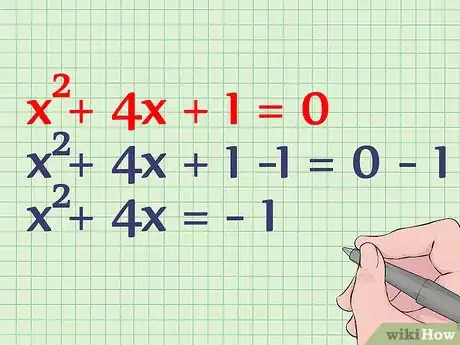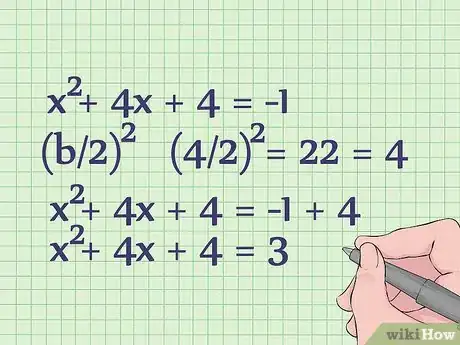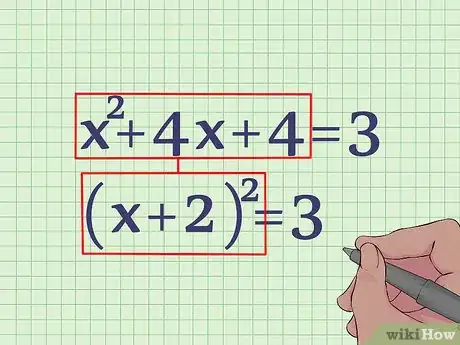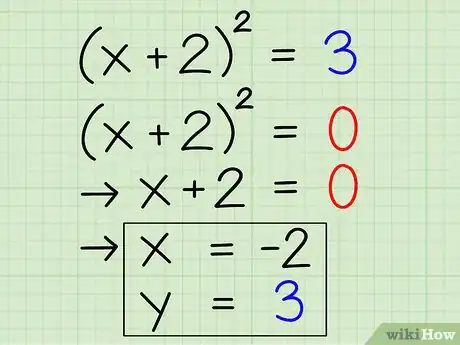Cómo encontrar el vértice de una ecuación cuadrática

Coescrito por David Jia

El vértice de una ecuación cuadrática o parábola es el punto más alto o más bajo de la gráfica correspondiente a dicha función. El vértice se encuentra en el plano de simetría de la parábola; cualquier cosa que suceda a la izquierda de este punto será un reflejo exacto de lo que sucede a la derecha. Si quieres hallar el vértice de una ecuación cuadrática, puedes utilizar la fórmula del vértice o completar el cuadrado.

Método 1

Método 1 de 2:
Utilizar la fórmula del vértice

1
Identifica los valores de a, b y c. En una ecuación cuadrática, el término x² = a, el término x = b, y la constante (el término sin variable) = c. Supongamos que queremos resolver la ecuación: y = x² + 9x + 18. En este ejemplo, a = 1, b = 9, y c = 18.
2
Utiliza la fórmula del vértice para hallar el valor x del vértice. El vértice también determina dónde se encuentra el eje de simetría de la ecuación (x). La fórmula para hallar el valor x del vértice de una ecuación cuadrática es x = -b/2a. Introduce los valores pertinentes para calcular x. Sustituye los valores de a y de b y resuelve:
- x=-b/2a
- x=-(9)/(2)(1)
- x=-9/2
3
Sustituye x en la ecuación original por su valor numérico para hallar el valor de y. Ahora que conoces x, solo tendrás que introducir su valor numérico en la fórmula original para hallar y. Puedes pensar en la fórmula para hallar el vértice de una función cuadrática de la siguiente forma: (x, y) = [(-b/2a), f(-b/2a)]. Esto simplemente significa que para calcular el valor de y es necesario despejar la incógnita x utilizando la fórmula, para después introducir el valor numérico hallado en la ecuación. Aquí podrás ver cómo hacerlo paso a paso:
- y = x² + 9x + 18
- y = (-9/2)² + 9(-9/2) +18
- y = 81/4 -81/2 + 18
- y = 81/4 -162/4 + 72/4
- y = (81 - 162 + 72)/4
- y = -9/4
4
Escribe los valores de x y de y en forma de coordenadas. Ahora que ya sabes que x = -9/2, e y = -9/4, solo tienes que escribir estos valores en forma de coordenadas: (-9/2, -9/4). El vértice de esta ecuación cuadrática es (-9/2, -9/4). Si tuvieses que representar esta parábola en una gráfica, el vértice hallado sería el mínimo de la curva, ya que el término x² es positivo.

Anuncio

Método 2

Método 2 de 2:
Completar el cuadrado

1
Escribe la ecuación. Completar el cuadrado es otra forma de hallar el vértice de una ecuación cuadrática. Si empleas este método, cuando llegues al final, podrás despejar las coordenadas de x y de y, en lugar de tener que introducir el valor de x en la ecuación original. Supongamos que estamos resolviendo la siguiente ecuación cuadrática: x² + 4x + 1 = 0.^{[1]
X
Fuente de investigación}
2
Divide cada término entre el coeficiente del término x². En este caso, el coeficiente de del término x² es 1, por lo que podrás saltarte este paso. Dividir cada término entre 1 no modificaría nada.
3
Pasa la constante a la derecha de la ecuación. La constante es el término que aparece sin coeficiente. En este caso, es 1. Pasa esta cifra la derecha de la ecuación restándolo de ambos lados del signo "=". Aquí puedes ver cómo hacerlo:^{[2]
X
Fuente de investigación}
- x² + 4x + 1 = 0
- x² + 4x + 1 -1 = 0 - 1
- x² + 4x = - 1
4
Completa el cuadrado al lado izquierdo de la ecuación. Para hacer esto, solo tienes que hallar (b/2)² sumar el resultado en ambos lados de la ecuación. Sustituye b por 4, ya que 4x es el término b de esta ecuación.
- (4/2)² = 2² = 4. Ahora, suma 4 a ambos lados de la ecuación para obtener lo siguiente:
  - x² + 4x + 4 = -1 + 4
  - x² + 4x + 4 = 3
5
Factoriza el lado izquierdo de la ecuación. Como puedes comprobar, x² + 4x + 4 es un cuadrado perfecto. Puedes expresarlo como (x + 2)² = 3
6
Utiliza este formato para hallar las coordenadas x e y. Puedes calcular la coordenada x igualando (x + 2)² a cero. Entonces, si (x + 2)² = 0, ¿cuál será el valor de x? La variable x deberá ser -2 para equilibrar el +2, por lo que la coordenada x es igual a -2. La coordenada y es el término constante que hay al otro lado de la ecuación. Por lo tanto, y es igual a -3, pues primero se debe pasar al lado izquierdo de la ecuación. También puedes simplificar el proceso utilizando el número dentro del paréntesis con el signo opuesto para hallar la coordenada x. El vértice de la ecuación x² + 4x + 1 es igual a (-2, -3).

Anuncio

Consejos

Asegúrate de identificar correctamente a, b y c.
Anota siempre todos los pasos de forma ordenada. De esta forma, no solo ayudarás a quien tenga que corregirte a que pueda ver todo el proceso resolutivo, sino que también te resultará más fácil detectar posibles errores.
Un proceso ordenado y claro debería garantizar un resultado correcto.

Anuncio

Advertencias

Escribe todo el proceso y compruébalo.
Asegúrate de hallar los términos a, b y c correctamente. Si te confundes en este paso, el resultado final será incorrecto.
No te estreses; resolver con soltura este tipo de ecuaciones puede requerir práctica.

Anuncio