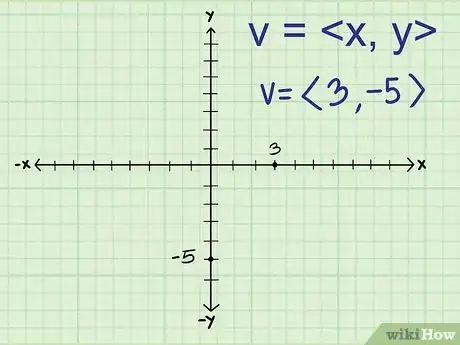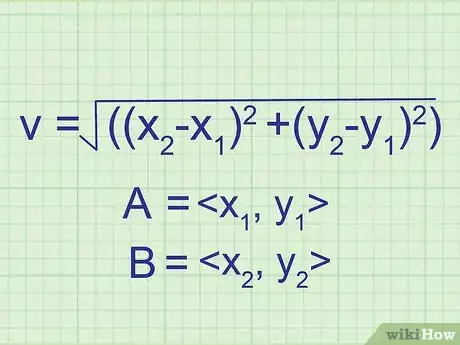Cómo encontrar la magnitud de un vector

Información del autor

Un vector es un objeto geométrico que posee una magnitud y una dirección.^{[1]
X
Fuente de investigación} La magnitud es la longitud del vector, mientras que la dirección indica hacia donde apunta el vector. Calcular la magnitud del vector es simple y solo debes seguir unos pasos sencillos. Otras operaciones importantes que puedes hacer con ellos son sumar y restar vectores, hallar el ángulo entre dos vectores y hallar el producto vectorial.

Método 1

Método 1 de 2:
Calcular la magnitud de un vector en el origen

1
Determina los componentes del vector. Todos los vectores se pueden expresar numéricamente en un sistema de coordenadas cartesianas a través de un componente horizontal (eje x) y un componente vertical (eje y).^{[2]
X
Fuente de investigación} Se escribe como un par ordenado $v=<x,y>$ $v=<x,y>$ .
- Por ejemplo, el vector de la imagen tiene un componente horizontal de 3 y un componente vertical de -5; por lo tanto, el par ordenado es <3, -5>.
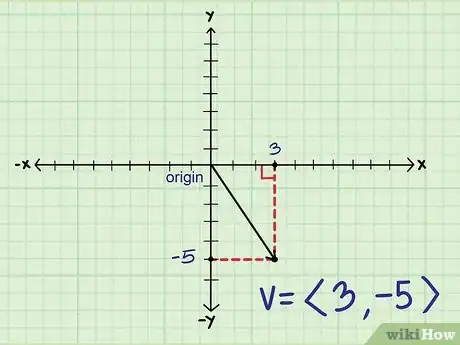
2
Dibuja un triángulo con el vector. Cuando dibujes los componentes vertical y horizontal, terminarás formando un triángulo rectángulo. La magnitud del vector es igual a la hipotenusa del triángulo, por lo tanto, puedes utilizar el teorema de Pitágoras para calcularla.
3
Reordena la ecuación del teorema de Pitágoras para calcular la magnitud. El teorema de Pitágoras establece que A² + B² = C², siendo "A" y "B" los componentes horizontal y vertical del triángulo y "C" la hipotenusa. Como la hipotenusa es el vector, tienes que resolver la ecuación para hallar el valor de "C".
- x² + y² = v²
- v = √(x² + y²))
4
Obtén la magnitud. Utilizando la ecuación anterior, ahora puedes reemplazar los números del par ordenado del vector para hallar la magnitud.
- Por ejemplo: v = √((3²+(-5)²))
- v =√(9 + 25) = √34 = 5,831
- No te preocupes si la respuesta no es un número entero: las magnitudes de los vectores pueden ser números decimales.

Método 2

Método 2 de 2:
Calcular la magnitud de un vector alejado del origen

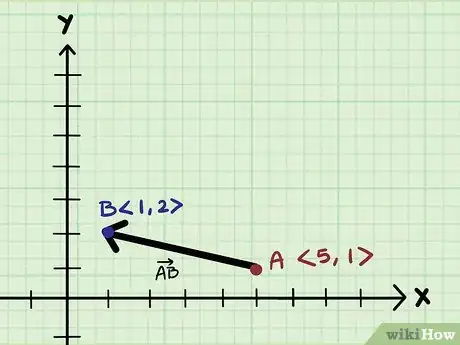
1
Determina los componentes de ambos puntos del vector. Todos los vectores se pueden expresar numéricamente en un sistema de coordenadas cartesianas a través de un componente horizontal (eje x) y un componente vertical (eje y).^{[3]
X
Fuente de investigación} Se escribe como un par ordenado $v=<x,y>$ $v=<x,y>$ . Si te proporcionan un vector que está alejado del origen del sistema de coordenadas cartesianas, deberás definir los componentes de ambos puntos del vector.
- Por ejemplo, el vector AB tiene un par ordenado para el punto A y el punto B.
- El punto A tiene un componente horizontal de 5 y un componente vertical de 1. Por lo tanto, el par ordenado es <5, 1>.
- El punto B tiene un componente horizontal de 1 y un componente vertical de 2. Por lo tanto, el par ordenado es <1, 2>.
2
Utiliza una fórmula modificada para obtener la magnitud. Debido a que ahora tienes que ocuparte de dos puntos diferentes, tendrás que restar los componentes x y y de cada punto para hallar la solución utilizando la ecuación v = √((x₂-x₁)² +(y₂-y₁)²).^{[4]
X
Fuente de investigación}
- El punto A es el par ordenado <x₁, y₁> y el punto B es el par ordenado 2 <x₂, y₂>
3
Obtén la magnitud. Reemplaza los números de tus pares ordenados y calcula la magnitud. Usando el ejemplo de la imagen, la ecuación deberá quedar así:
- v = √((x₂-x₁)² +(y₂-y₁)²)
- v = √((1-5)² +(2-1)²)
- v = √((-4)² +(1)²)
- v = √(16+1) = √(17) = 4,12
- No te preocupes si la respuesta no es un número entero. Las magnitudes de los vectores pueden ser números decimales.