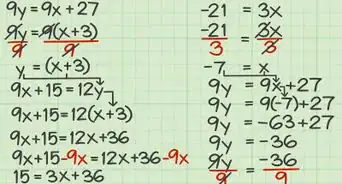Este artículo fue coescrito por David Jia. David Jia es tutor académico y el fundador de LA Math Tutoring, una empresa de tutoría privada con sede en Los Ángeles, California. Con más de 10 años de experiencia en enseñanza, David trabaja con estudiantes de todas las edades y grados en diversas materias, así como en asesoría para postulaciones universitarias y preparación para pruebas como el SAT, ACT, ISEE y más. Luego de obtener una calificación perfecta de 800 en matemáticas y 690 en inglés en el SAT, David recibió la beca Dickinson de la Universidad de Miami, donde se graduó con una licenciatura en Administración de Empresas. Asimismo, ha trabajado como instructor para videos en línea para empresas de libros de texto como Larson Texts, Big Ideas Learning y Big Ideas Math.
Este artículo ha sido visto 400 692 veces.
Una ecuación cuadrática (o de segundo grado) es una ecuación polinómica en una variante simple donde a máxima potencia de la variable es 2. Existen tres formas principales de resolver ecuaciones de segundo grado: 1)factorizar la ecuación (si es posible), 2) utilizar la fórmula cuadrática, o 3) completar el cuadrado. Si quieres aprender a dominar estos tres métodos, solo tienes que seguir los siguientes pasos.
Pasos
Método 1
Método 1 de 3:
Factorizar la ecuación
-
1Combina todos los términos semejantes y transpórtalos a un lado de la ecuación. El primer paso para factorizar una ecuación es transportar todos los términos a un lado de la ecuación, manteniendo positivo el término . Para combinar los términos, suma o resta todos los términos , los términos , y las constantes (términos enteros), transportándolos a un lado de la ecuación hasta que no quede nada en el otro lado. Una vez que te quedes sin términos restantes, simplemente escribe "0" en ese lado del signo igual (=). A continuación, te mostraremos cómo debes hacerlo:[1]
-
2Factoriza la expresión. Para factorizar la expresión, tienes que utilizar los factores del término (3) y los factores del término constante (-4) para que se multipliquen y luego se sumen al término medio (-11). A continuación, te mostraremos cómo debes hacerlo:
- Dado que solo tiene un conjunto de posibles factores, y puedes colocarlos entre paréntesis:.
- Luego, realiza un proceso de descarte para reemplazar los factores de 4 y encontrar una combinación que cuando se multiplique dé como resultado “-11x”. Puedes utilizar las combinaciones: 4 y 1, o 2 y 2, ya que, al multiplicar ambas, se obtiene 4. Solo recuerda que uno de los términos debe ser negativo, ya que el término es -4.
- Haz varias pruebas y empieza con esta combinación de factores: . Si los multiplicas, obtendrás: . Si combinas los términos y , te da , que es el término medio que estamos buscando. Con esto, acabas de factorizar la ecuación.
- Como ejemplo de pruebas, intenta revisar una combinación de factorización para que sea un error (no funcione): = . Si combinas estos términos, obtendrás: . Aunque al multiplicar los factores -2 y 2, obtenemos -4, el término medio no funciona porque se necesitaba obtener , y no .
-
3Iguala cada conjunto entre paréntesis a cero como ecuaciones separadas. Al hacerlo, encontrarás dos valores para que harán que toda la ecuación sea igual a cero = 0. Ahora que la ecuación está factorizada, todo lo que tienes que hacer es poner la expresión en cada conjunto de paréntesis igual a cero. Pero, ¿por qué? Porque para obtener cero multiplicando, tenemos el "principio, regla o propiedad" que un factor debe ser cero, entonces al menos uno de los factores entre paréntesis, como debe ser cero; (3x + 1) o bien (x - 4) debe ser igual a cero. Por lo tanto, se escribe y también
-
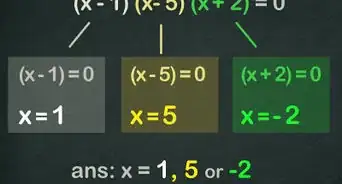
4Resuelve cada ecuación "cero" de manera independiente. En una ecuación de segundo grado, existirán dos posibles valores para “x”. Encuentra x para cada posible valor de x uno por uno por medio de aislar la variable, y escribe ambos valores para x como la solución final. A continuación, se muestra cómo debes hacerlo:
- Resolver 3x + 1 = 0 =
- 3x = -1 ... sustrayendo
- 3x/3 = -1/3 ... dividiendo
- x = -1/3 ... simplificado
- Resuelve x - 4 = 0
- x = 4 sustrayendo
- x = (-1/3, 4) ... haciendo un conjunto de soluciones posibles, separadas, es decir, x = -1/3, or x = 4 parece estar bien.
- Resolver 3x + 1 = 0 =
-
5Revisa x = -1/3 en (3x + 1)(x – 4) = 0:
Se tiene (3[-1/3] + 1)([-1/3] – 4) ?=? 0 ..... sustituyendo (-1 + 1)(-4 1/3) ?=? 0 ..... simplificando (0)(-4 1/3) = 0 ..... multiplicando por lo tanto 0 = 0 ..... Sí, x = -1/3 funciona. -
6Revisa x = 4 en (3x + 1)(x - 4) = 0:
Se tiene (3[4] + 1)([4] – 4) ?=? 0 ..... sustituyendo (13)(4 – 4) ?=? 0 ..... simplificando (13)(0) = 0 ..... multiplicando 0 = 0 ..... Sí, x = 4 funciona.- Por lo tanto, ambas soluciones se "comprueban" por separado, y se verifica que ambas funcionan y que son correctas para dos soluciones diferentes.
Método 2
Método 2 de 3:Utilizar la fórmula cuadrática
-
1Combina todos los términos semejantes y transpórtalos a un lado de la ecuación. Transporta todos los términos a un lado del signo igual (=), manteniendo positivo el término . Escribe los términos en orden descendente de grados, de modo que el término " venga primero, seguido del término “x” y del término constante. A continuación, te mostramos cómo debes hacerlo:
- 4x2 - 5x - 13 = x2 -5
- 4x2 - x2 - 5x - 13 +5 = 0
- 3x2 - 5x - 8 = 0
-
2Escribe la fórmula cuadrática. La fórmula cuadrática es la siguiente: [2]
-
3Identifica los valores de “a”, “b”, y “c” en la ecuación de segundo grado. La variable “a” es el coeficiente del término "x2", la “b” es el coeficiente del término “x”, y la “c” es la constante. Para la ecuación: 3x2 -5x - 8 = 0, a = 3, b = -5, y c = -8. Escribe todo esto.
-
4Reemplaza los valores de “a”, “b”, y “c” en la ecuación. Ahora que cuentas con los valores de las tres variables, reemplázalas en la ecuación de la siguiente manera:
- {-b +/-√ (b2 - 4ac)}/2
- {-(-5) +/-√ ((-5)2 - 4(3)(-8))}/2(3) =
- {-(-5) +/-√ ((-5)2 - (-96))}/2(3)
-
5Realiza tus cálculos. Después de que hayas reemplazado los números, realiza los cálculos restantes para simplificar los signos positivos o negativos. Multiplica o eleva al cuadrado los términos restantes. A continuación, te mostramos cómo debes hacerlo:
- {-(-5) +/-√ ((-5)2 - (-96))}/2(3) =
- {5 +/-√(25 + 96)}/6
- {5 +/-√(121)}/6
-
6Simplifica la raíz cuadrada. Si el número bajo el símbolo radical es un cuadrado perfecto, obtendrás un número entero. Si no lo es, entonces simplifícalo a su versión radical más simple. Si es negativo, y estás seguro de que debe ser negativo, entonces las raíces serán complejas. Para el siguiente ejemplo: √(121) = 11, puedes escribir: x = (5 +/- 11)/6.
-
7Encuentra dos respuestas. Si has eliminado el símbolo de la raíz cuadrada, entonces puedes continuar hasta que encuentres ambos valores (positivo y negativo) para “x”. Ahora que ya tienes: (5 +/- 11)/6, puedes escribir dos opciones:
- (5 + 11)/6
- (5 - 11)/6
-
8Obtén ambas respuestas (una positiva y otra negativa). Simplemente realiza los siguientes cálculos:
- (5 + 11)/6 = 16/6
- (5-11)/6 = -6/6
-
9Simplifica. Para simplificar cada respuesta, simplemente divídelas por el número más grande que divida igualmente ambos números. Divide la primera fracción entre 2 y divide la segunda entre 6 para que obtengas los valores para “x”.
- 16/6 = 8/3
- -6/6 = -1
- x = (-1, 8/3)
Método 3
Método 3 de 3:Completar el cuadrado
-
1Traslada todos los términos a un lado de la ecuación. Asegúrate de que el término “a” o "x2" sea positivo. A continuación, te mostraremos cómo debes hacerlo:[3]
- 2x2 - 9 = 12x =
- 2x2 - 12x - 9 = 0
- En esta ecuación, el término “a” es 2, el término “b” es -12, y el término “c” es -9.
-
2Transporta el término “c” o constante al otro lado. El término constante es el término numérico sin una variable. Transpórtalo hacia el lado derecho de la ecuación:
- 2x2 - 12x - 9 = 0
- 2x2 - 12x = 9
-
3Divide ambos lados por el coeficiente del término “a” o "x2". Si "x2" no presenta un término adelante, simplemente tiene un coeficiente de 1, por lo que puedes saltarte este paso. En este caso, tendrás que dividir todos los términos entre 2, de la siguiente manera:
- 2x2/2 - 12x/2 = 9/2 =
- x2 - 6x = 9/2
-
4Divide “b” entre dos, elévalo al cuadrado y suma el resultado en ambos lados. El término “b” en este ejemplo es -6. A continuación, te mostramos cómo debes hacerlo:
- -6/2 = -3 =
- (-3)2 = 9 =
- x2 - 6x + 9 = 9/2 + 9
-
5Simplifica ambos lados. Factoriza los términos del lado izquierdo para que obtengas: (x-3)(x-3), o (x-3)2. Suma los términos en el lado derecho para que obtengas: 9/2 + 9 o 9/2 + 18/2, lo que equivale a 27/2.
-
6Encuentra la raíz cuadrada en ambos lados. La raíz cuadrada de (x-3)2 es simplemente (x-3). Puedes escribir la raíz cuadrada de 27/2 como: ±√(27/2). Por lo tanto: x - 3 = ±√(27/2).
-
7Simplifica el radical y encuentra el valor de “x”. Para simplificar ±√(27/2), busca un cuadrado perfecto dentro de los números 27 y 2 o de sus factores. El cuadrado perfecto 9 se encuentra dentro de 27, ya que: 9 x 3 = 27. Saca el número 9 y escribe el número 3 (su raíz cuadrada) al margen del signo radical. Deja el número 3 en el numerador de la fracción debajo del signo radical, ya que el factor de 27 no se puede sacar, y deja el número 2 en la parte inferior. Luego, transporta la constante 3 del lado izquierdo de la ecuación al lado derecho, y escribe ambos valores para “x”:
- x = 3 + (3√6)/2
- x = 3 - (3√6)/2
Consejos
- Como puedes ver, el signo radical no desapareció por completo. Por lo tanto, los términos en el numerador no se pueden combinar (porque no son términos semejantes). Entonces, no hay razón para dividir el signo +/-. En vez de eso, lo dividimos a factores comunes, pero SOLO si el factor es común para ambas constantes Y para el coeficiente del radical.
- Si el número bajo la raíz cuadrada no es un cuadrado perfecto, entonces los últimos pasos difieren un poco. Por ejemplo:
- Si el término "b" es un número par, la fórmula sería la siguiente: {-(b/2) +/- √(b/2)-ac}/a.
Referencias
Acerca de este wikiHow
Para resolver ecuaciones cuadráticas, primero combina todos los términos semejantes y colócalos en uno de los lados de la ecuación. Luego factoriza la expresión e iguala a 0 cada conjunto entre paréntesis, como si fueran ecuaciones separadas. Por último, resuelve cada ecuación en forma individual para encontrar los dos posibles valores de x. ¡Desplázate hacia abajo si quieres aprender a resolver ecuaciones cuadráticas usando la fórmula cuadrática!




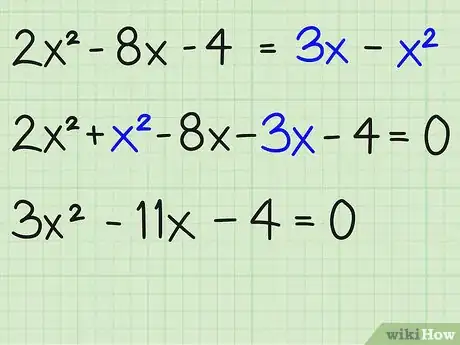





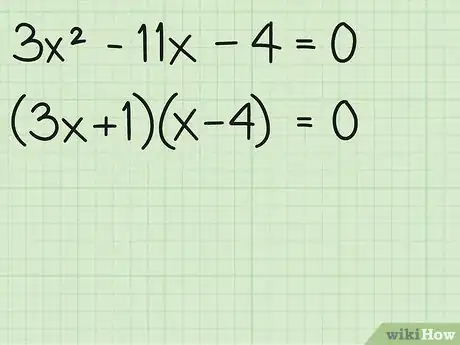











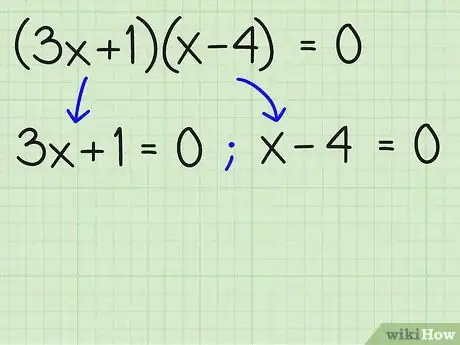


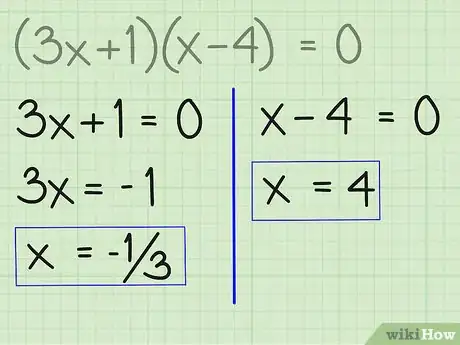
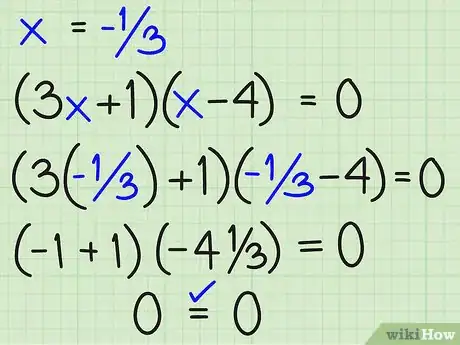
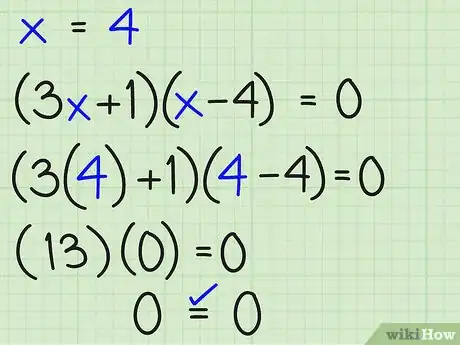
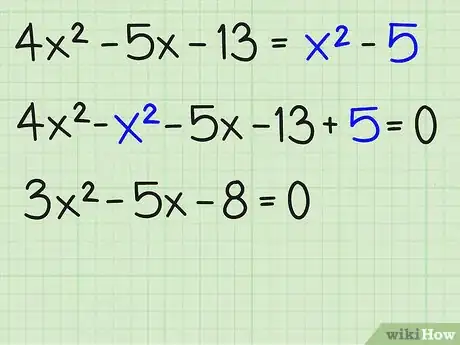
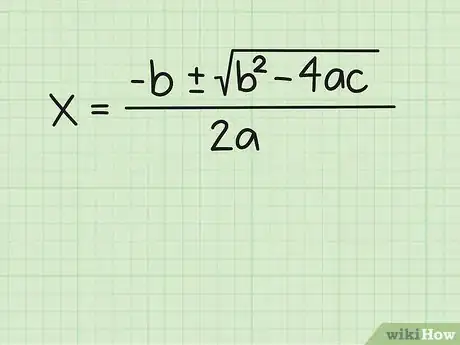

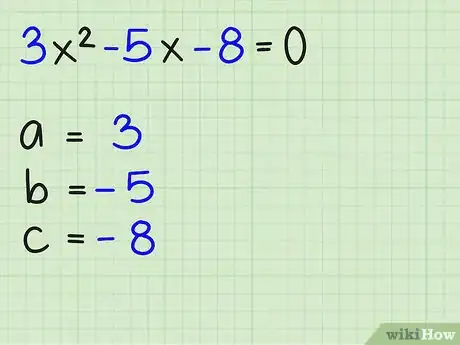
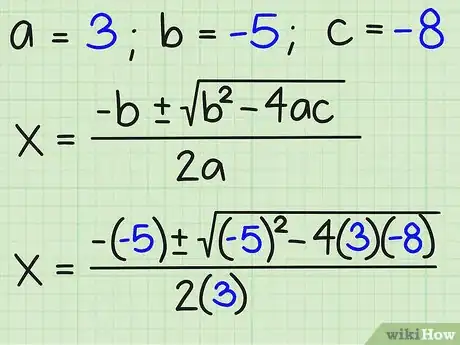
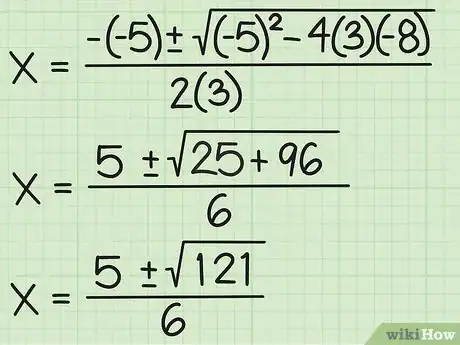
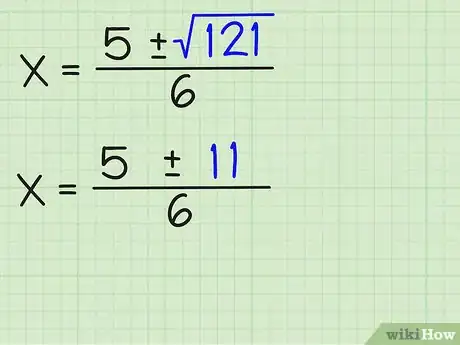

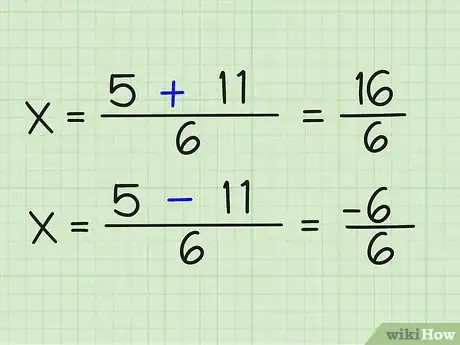

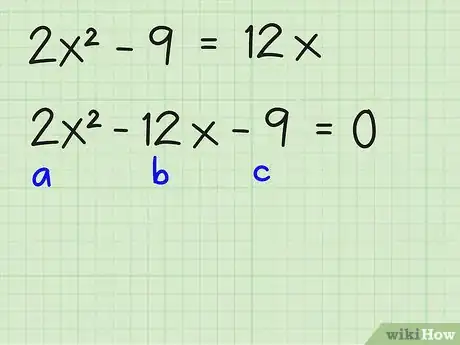
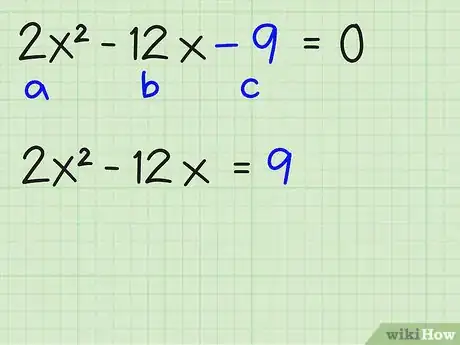
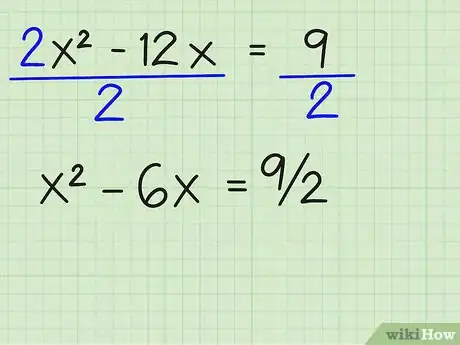
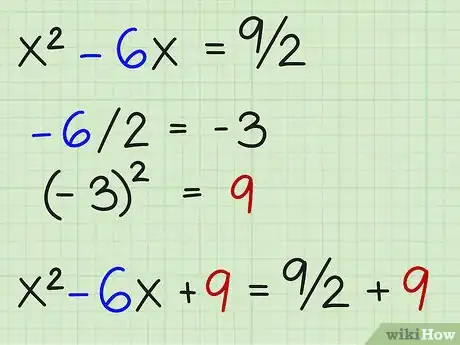
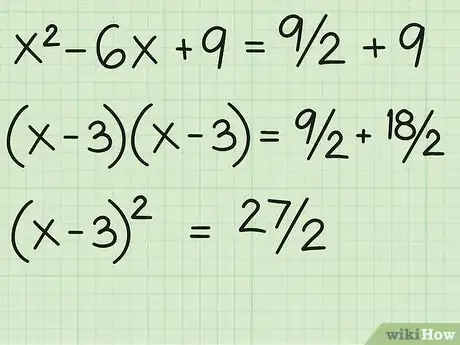
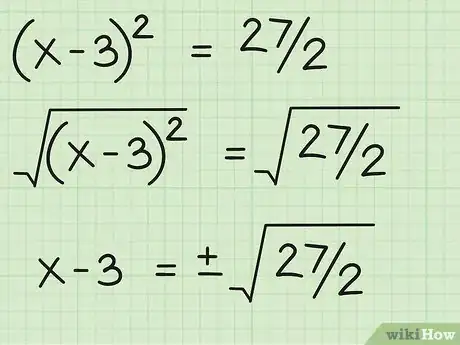
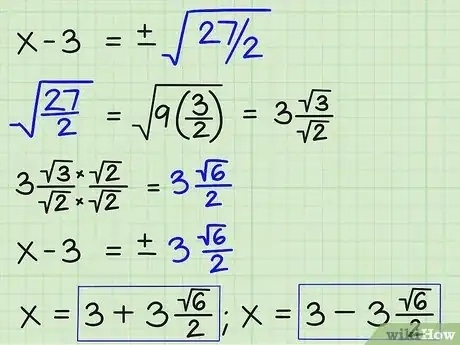



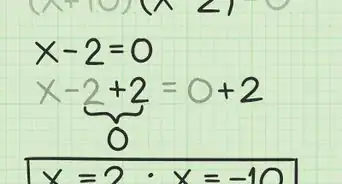
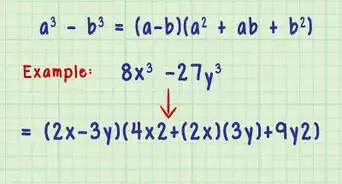
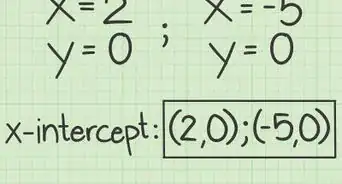
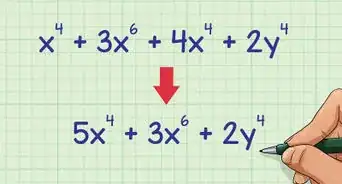
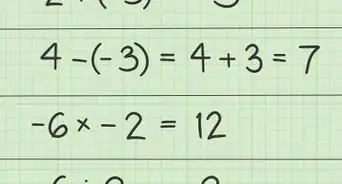
-Step-31-Version-2.webp)