Nuestro equipo de editores e investigadores capacitados han sido autores de este artículo y lo han validado por su precisión y amplitud.
wikiHow's Content Management Team revisa cuidadosamente el trabajo de nuestro personal editorial para asegurar que cada artículo cumpla con nuestros altos estándares de calidad.
Este artículo ha sido visto 45 288 veces.
Resolver operaciones con exponentes es una habilidad básica que todo estudiante debe aprender en introducción al álgebra. Los exponentes que uno ve normalmente son números enteros y, en ocasiones, fracciones. Casi nunca aparecen como decimales. Cuando veas un exponente con números decimales, deberás convertirlos a una fracción. Luego, podrás usar las reglas y leyes correspondientes a operaciones exponenciales para calcular la expresión.
Pasos
Parte 1
Parte 1 de 3:Calcular un exponente decimal
-
1Convierte el decimal a una fracción. Para convertir un decimal a una fracción, deberás tener en cuenta el valor posicional. El denominador de la fracción determinará el valor posicional. El numerador contendrá los dígitos de dicho decimal.[1]
- Por ejemplo, en el caso de la expresión exponencial , deberás convertir a una fracción. Como el decimal llega hasta el lugar de las centésimas, la fracción correspondiente será .
-
2Simplifica la fracción cuando sea posible. Como vas a calcular la raíz correspondiente al denominador de la fracción del exponente, es mejor que el denominador sea lo más pequeño posible. Para ello, hay que simplificar la fracción. Si la fracción es un número mixto (es decir, el exponente original era un decimal mayor que 1), reescríbelo como fracción impropia.
- Por ejemplo, la fracción se reduce a . Por lo tanto, .
-
3Reescribe el exponente como una expresión de multiplicación. Para hacerlo, convierte el numerador en un número entero y multiplícalo por la fracción unitaria. La fracción unitaria es una fracción con el mismo denominador, pero con 1 como numerador.
- Por ejemplo, como , puedes reescribir la expresión exponencial como .
-
4Reescribe el exponente como la potencia de una potencia. Recuerda que multiplicar dos exponentes es como calcular la potencia de una potencia. Por lo tanto, equivale a .[2]
- Por ejemplo, .
-
5Reescribe la base como una expresión radical. Elevar un número a un exponente racional equivale a obtener la raíz correspondiente de ese número. Por lo tanto, reescribe la base y el primer exponente como una expresión radical.
- Por ejemplo, como , puedes reescribir la expresión de la forma .[3]
-
6Calcula la expresión radical. Recuerda que el índice (el número pequeño que va afuera del signo radical) indica la raíz que estás buscando. Si los números son complicados, la mejor forma de hacerlo es usando la función de la calculadora científica.
- Por ejemplo, para calcular , es necesario determinar qué número multiplicado por sí mismo 4 veces es igual a 81. Como , sabes que . Por lo tanto, la expresión exponencial ahora se convertirá en .
-
7Calcula el exponente restante. Ahora tendrás un número entero como exponente, así que los cálculos finales serán mucho más sencillos. Si los números son demasiado grandes, siempre puedes usar una calculadora.
- Por ejemplo, . Por lo tanto, .
Anuncio
Parte 2
Parte 2 de 3:Resolver un problema de ejemplo
-
1Calcula la siguiente expresión exponencial: .
-
2Convierte el decimal a una fracción. Como es mayor que 1, la fracción será un número mixto.
- El decimal es igual a , so .
-
3Simplifica la fracción de ser posible. También deberás convertir los números mixtos a fracciones impropias.
- Como se reduce a , .
- Convirtiendo a una fracción impropia, tendrás . Por lo tanto, .
-
4Reescribe el exponente como una expresión de multiplicación. Como , puedes reescribir la expresión de la forma .
-
5Reescribe el exponente como potencia de una potencia. De este modo, .
-
6Reescribe la base como una expresión radical. ; por lo tanto, puedes reescribir la expresión como .
-
7Calcula la expresión radical. . Por lo tanto, la expresión ahora se convertirá en .
-
8Calcula el exponente final. . Por lo tanto, .Anuncio
Parte 3
Parte 3 de 3:Interpretar los exponentes
-
1Reconoce una expresión exponencial. Las expresiones exponenciales tienen una base y un exponente. La base es el número grande de la expresión. El exponente es el número pequeño.[4]
- Por ejemplo, en la expresión , es la base y es el exponente.
-
2Identifica las partes de una expresión exponencial. La base es el número a multiplicar. El exponente te indica cuántas veces se usará la base como factor en la expresión.[5]
- Por ejemplo, .
-
3Identifica los exponentes racionales. Los exponentes racionales también se conocen como exponentes fraccionales. Son exponentes en forma de fracción.[6]
- Por ejemplo, .
-
4Comprende las relaciones entre radicales y exponentes racionales. Elevar un número a la potencia de equivale a calcular la raíz cuadrada del número. Así, . Lo mismo ocurre con otras raíces y exponentes. El denominador del exponente te indicará qué raíz hay que calcular:[7]
- Por ejemplo, . Sabes que 3 es la raíz cuarta de 81 ya que
-
5Aprende lo que establece la ley de los exponentes acerca de la potencia de una potencia. Esta ley establece que . En otras palabras, elevar un exponente a otra potencia equivale a multiplicar esos dos exponentes.[8]
- Si trabajas con exponentes racionales, esta ley se puede representar de la siguiente manera: , ya que .[9]
Anuncio
Referencias
- ↑ http://www.coolmath.com/prealgebra/02-decimals/05-decimals-converting-decimal-to-fraction-01
- ↑ http://www.mathsisfun.com/algebra/exponent-fractional.html
- ↑ http://mathforum.org/library/drmath/view/55562.html
- ↑ https://www.mathsisfun.com/exponent.html
- ↑ https://www.mathsisfun.com/exponent.html
- ↑ http://www.mathsisfun.com/algebra/exponent-fractional.html
- ↑ http://www.purplemath.com/modules/exponent5.htm
- ↑ http://brownmath.com/alge/expolaws.htm# Multiply
- ↑ http://mathforum.org/library/drmath/view/55562.html








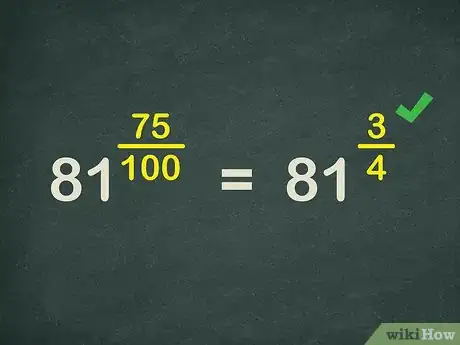


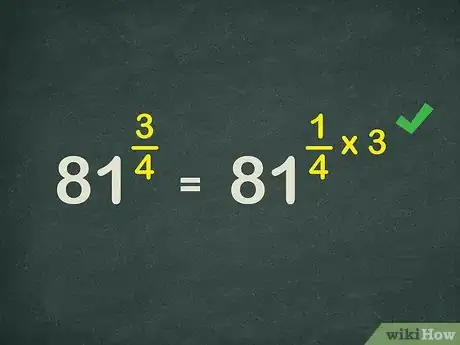


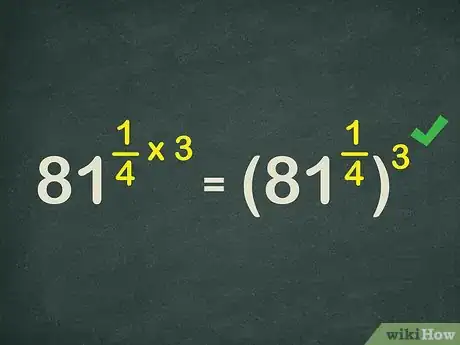



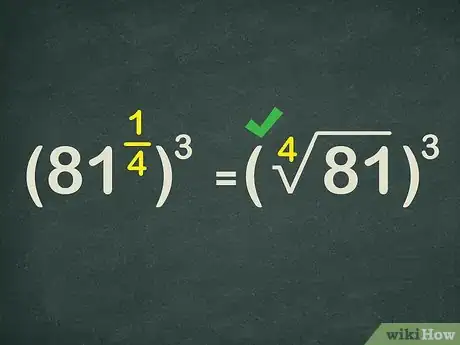
![81^{{{\frac {1}{4}}}}={\sqrt[ {4}]{81}}](./images/1729896335-b37415d73d383d0450962dda1cf0ddb2e0da0452.webp)
![({\sqrt[ {4}]{81}})^{{3}}](./images/1878007873-79a4e12743be369be81296fe2aeabd97c70cb9ab.webp)
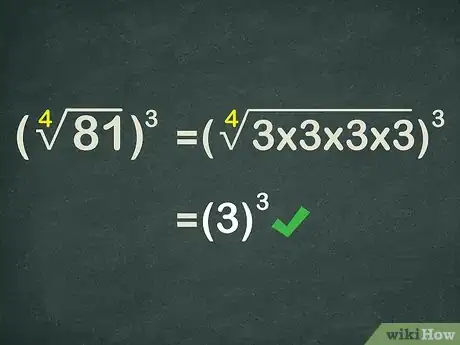
![{\sqrt[ {x}]{y}}](./images/1733107567-58c28156258e3c4cf15e8af14abcc0163150e3e6.webp)
![{\sqrt[ {4}]{81}}](./images/1841110937-44f5722ccf46fec0200534e84bda483bc2b726b1.webp)

![{\sqrt[ {4}]{81}}=3](./images/1590632178-44d91764f62522cec7024ef6481f0b83305f17e9.webp)

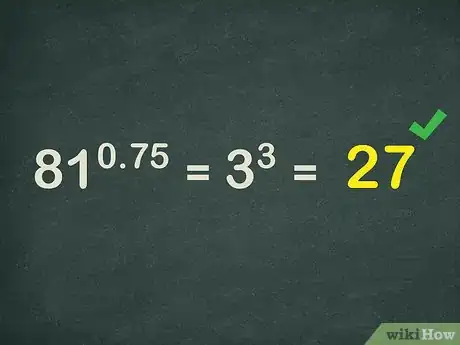


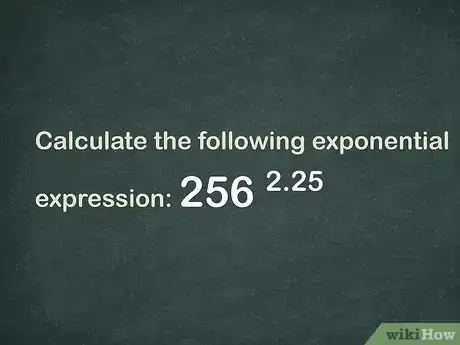

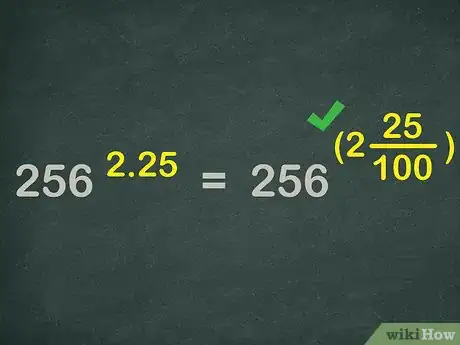




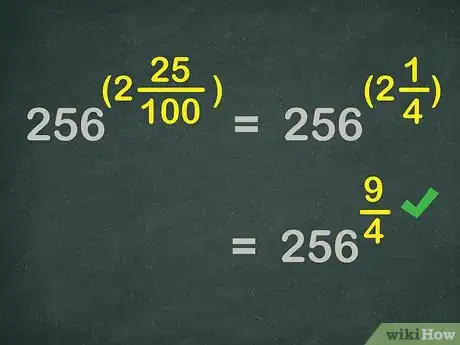




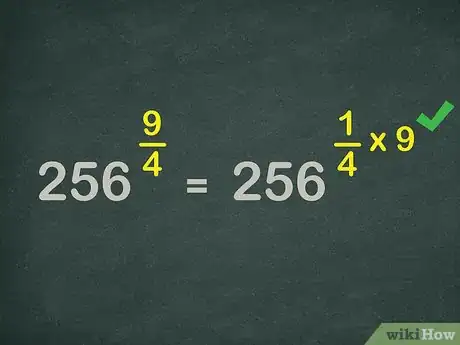


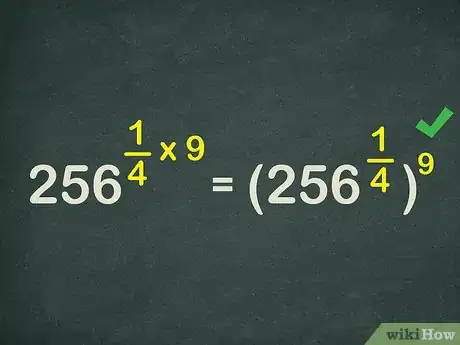

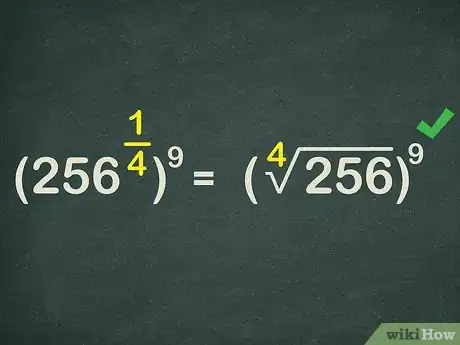
![256^{{{\frac {1}{4}}}}={\sqrt[ {4}]{256}}](./images/2244026551-cb9c02c237d2aeb16bc1fd12eaf89cbde1d683a4.webp)
![({\sqrt[ {4}]{256}})^{{9}}](./images/1315184169-261990049bf6155622a73330e280af3d17084588.webp)
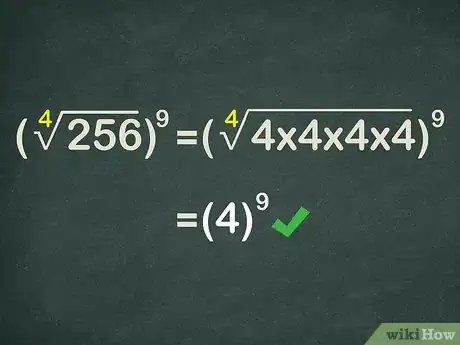
![{\sqrt[ {4}]{256}}=4](./images/2117541890-55bb3e8f3f86ce5c35d5f18ddd8f486e75e67476.webp)

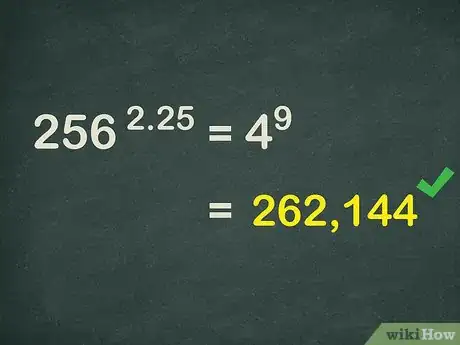






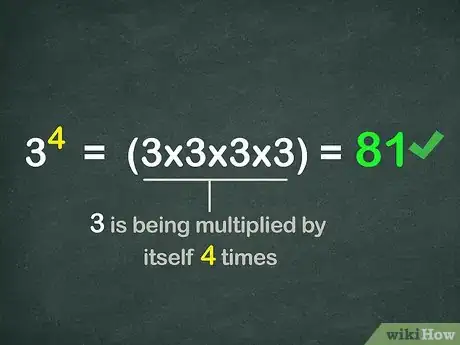



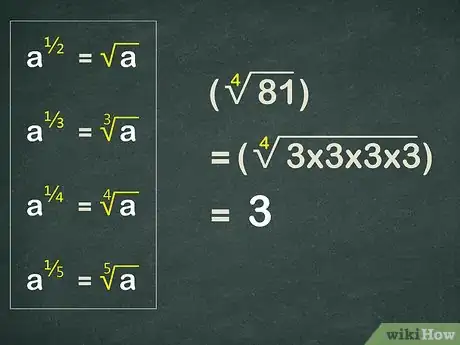


![x^{{{\frac {1}{3}}}}={\sqrt[ {3}]{x}}](./images/2160271401-759eade6ce89e27b301ccdcd83d7e8858827b8e2.webp)
![x^{{{\frac {1}{4}}}}={\sqrt[ {4}]{x}}](./images/1811226489-625ea5fe7631555b2fc23ac21f595d7c20633ec9.webp)
![x^{{{\frac {1}{5}}}}={\sqrt[ {5}]{x}}](./images/1955799054-788c8c448ea3cf9b81867b10ba6bbb1a47abb388.webp)
![81^{{{\frac {1}{4}}}}={\sqrt[ {4}]{81}}=3](./images/2053775506-0af496f05893da79ec2c45b4ebebabce0930dce0.webp)
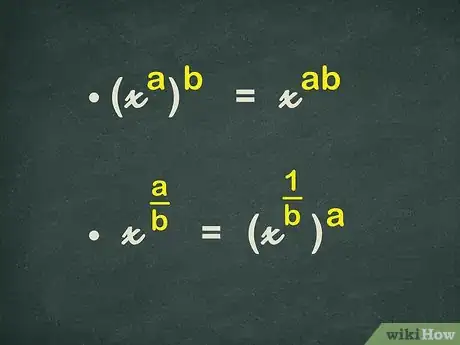







-Step-31-Version-2.webp)




wikiHow's Content Management Team revisa cuidadosamente el trabajo de nuestro personal editorial para asegurar que cada artículo cumpla con nuestros altos estándares de calidad. Este artículo ha sido visto 45 288 veces.