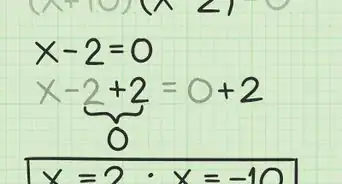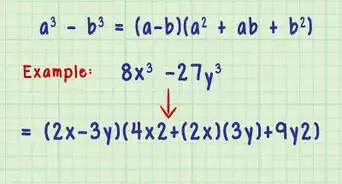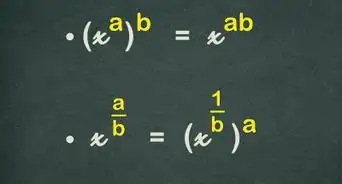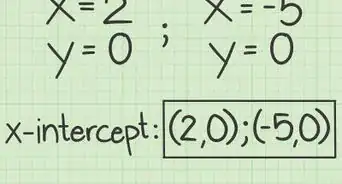Cómo aprender álgebra

Coescrito por Daron Cam

Aprender álgebra puede parecerte intimidante, pero una vez que la domines, ¡dejará de ser difícil! ¡Tan solo tendrás que seguir el orden para culminar las partes de la ecuación y mantener tu trabajo organizado a fin de evitar los errores!

Parte 1

Parte 1 de 5:
Aprender las reglas básicas del álgebra

1
Revisa tus operaciones matemáticas básicas. Para aprender álgebra, debes conocer las habilidades matemáticas básicas tales como la suma, la resta, la multiplicación y la división. Esta matemática de escuela primaria es esencial para poder aprender álgebra. Si no has dominado estas habilidades, será difícil abordar los conceptos más completos que se enseñan en álgebra. Si necesitas repasar estas operaciones, lee este artículo de wikiHow, que habla acerca de las habilidades de matemática básicas.
- No es necesario dominar a la perfección estas operaciones básicas en tu mente para poder resolver los problemas de álgebra. Muchas clases de álgebra te permitirán utilizar una calculadora para ahorrar tiempo cuando resuelvas estas operaciones simples. Sin embargo, por lo menos debes saber cómo realizar estas operaciones sin utilizar una calculadora para cuando no te permitan hacerlo.
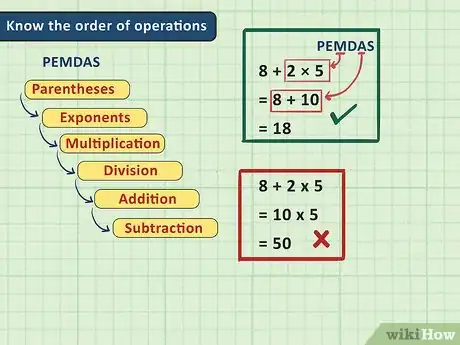
2
Conoce el orden de las operaciones. Una de las cosas más complicadas acerca de la resolución de una ecuación algebraica como principiante es saber dónde empezar. Por suerte, existe un orden específico para resolver estos problemas: primero resuelve las operaciones matemáticas que están entre paréntesis, luego los exponentes, la multiplicación, la división, la suma y, por último, la resta. Una herramienta para recordar este orden de operaciones son las siglas PEMDSR. Para recapitular, el orden de las operaciones es el siguiente:
- Paréntesis
- Exponentes
- Multiplicación
- División
- Suma
- Resta
- En álgebra, el orden de las operaciones es importante porque realizar estas operaciones en un problema algebraico en el orden incorrecto a veces puede afectar la respuesta. Por ejemplo, en este problema matemático 8 + 2 × 5, si sumamos 2 a 8 primero, obtendremos 10 × 5 = 50, pero si multiplicáramos 2 y 5 primero, obtendremos 8 + 10 = 18. Solo la segunda respuesta es la correcta.
3
Aprende a utilizar los números negativos. En álgebra, es común utilizar números negativos, de modo que es sensato revisar información sobre cómo sumar, restar, multiplicar y dividir números negativos antes de comenzar a aprender álgebra. Estos son algunos elementos básicos sobre los números negativos que debes tener en cuenta. Si necesitas más información, busca en Internet artículos sobre cómo sumar, restar, multiplicar y dividir números negativos.
- En una recta numérica, una versión negativa de un número está a la misma distancia del cero como la versión positiva, pero en la dirección opuesta.
- Sumar dos números negativos hace al número más negativo (es decir, los dígitos serán mayores, pero dado que el número es negativo, cuenta como menor).
- Dos signos negativos se cancelan, ya que restar un número negativo es lo mismo que sumar uno positivo
- Multiplicar o dividir dos números negativos da una respuesta positiva.
- Multiplicar o dividir un número positivo y uno negativo da una respuesta negativa.
4
Aprender a ordenar problemas extensos. Si bien los problemas algebraicos simples pueden ser fáciles de resolver, los más complicados pueden requerir muchos pasos. Para evitar errores, mantén tu trabajo organizado comenzando en una línea nueva cada vez que continúes con la resolución del problema. Si tienes una ecuación de dos lados, escribe todos los signos igual ("=") debajo uno del otro. De esta manera, si cometes un error en algún punto, será mucho más fácil encontrarlo y corregirlo.
- Por ejemplo, para resolver la ecuación 9/3 -5 +3 × 4, podemos organizar el problema así:
  
  9/3 - 5 + 3 × 4
  
  9/3 - 5 + 12
  
  3 - 5 + 12
  
  3 + 7
  
  10

Parte 2

Parte 2 de 5:
Comprender las variables

1
Busca los símbolos que no sean números. En álgebra, comenzarás a ver letras y símbolos que aparecen en tus problemas matemáticos en lugar de solo números. Estos reciben el nombre de "variables". Las variables no solo son tan confusas como pueden parecer el principio, sino que son formas de mostrar números con valores desconocidos. Los siguientes son algunos ejemplos comunes de las variables en álgebra:
- Las letras como x, y, z, a, b, c
- Las letras griegas como theta o θ
- Ten en cuenta que no todos los símbolos son conocidos como variables, por ejemplo, pi, o π, siempre es igual a 3,1459.
2
Imagina que las variables son números "desconocidos". Como se mencionó anteriormente, las variables son básicamente números con valores desconocidos. En otras palabras, hay un número que puede colocarse en el lugar de la variable para hacer que la ecuación funcione. Por lo general, en un problema algebraico tu objetivo es averiguar el valor de la variable. Imagina que es un "número misterioso" que intentas descubrir.
- Por ejemplo, en la ecuación 2x + 3 = 11, x es nuestra variable. Esto significa que hay un valor que va en el lugar de x para hacer que el lado izquierda de la ecuación sea igual a 11. Dado que 2 × 4 + 3 = 11, en este caso, x = 4.
- Una manera sencilla de comenzar a comprender las variables es reemplazarlas con signos de interrogación en los problemas algebraicos. Por ejemplo, podemos volver a escribir la ecuación 2 + 3 + x = 9 como 2 + 3 + ? = 9. Esto facilita la comprensión de lo que tratamos de hacer: solo necesitamos averiguar qué número sumar a 2 + 3 = 5 para obtener 9. Desde luego, una vez más la respuesta es 4.
3
Si una variable aparece más de una vez, simplifícalas. ¿Qué haces si una variable aparece más de una vez en una ecuación? Si bien esta situación puede parecer difícil de resolver, en realidad puedes tratar las variables como lo harías con números normales. Es decir, puedes sumarlas, restarlas etc. siempre y cuando solo combines aquellas que sean semejantes. En otras palabras, x + x = 2x, pero x + y no es igual a 2xy.
- Por ejemplo, veamos la ecuación 2x + 1x = 9. En este caso, podemos sumar 2x y 1x para obtener 3x = 9. Dado que 3 x 3 = 9, sabemos que x = 3.
- Una vez más ten en cuenta que solo puedes sumar las mismas variables. En la ecuación 2x + 1y = 9, no podemos combinar 2x y 1y, puesto que las dos variables son diferentes.
- Esto también se aplica para cuando una variable tiene un exponente distinto que otra. Por ejemplo, en la ecuación 2x + 3x² = 10, no podemos combinar 2x y 3x², puesto que las variables x tienen exponentes diferentes. Lee el artículo "Cómo sumar exponentes" para obtener más información.

Parte 3

Parte 3 de 5:
Aprender a resolver ecuaciones mediante el método de cancelación

1
Trata de aislar la variable en las ecuaciones algebraicas. Resolver una ecuación algebraica generalmente significa determinar lo que es una variable. Las ecuaciones algebraicas generalmente se establecen con números o variables en ambos lados, de la siguiente manera: x + 2 = 9 × 4. Para hallar la variable, necesitas aislarla a un lado del signo igual. Lo que quede en el otro lado del signo igual será la respuesta.
- En el ejemplo (x + 2 = 9 × 4), para aislar x en el lado izquierdo de la ecuación, deberemos deshacernos del "+ 2". Para hacerlo, simplemente restaremos 2 de ese lado, quedándonos con x = 9 × 4. Sin embargo, para mantener iguales ambos lados de la ecuación, también necesitaremos restar 2 del otro lado. Esto nos deja con x = 9 × 4 - 2. Siguiendo el orden de las operaciones, primero multiplicamos y luego restamos lo que nos da una respuesta de x = 36 - 2 = 34.
2
Cancela la suma con la resta (y viceversa). Como vimos anteriormente, aislar x en un lado del signo igual generalmente significa deshacerse del número que está a su lado. Para hacerlo, desarrollamos la operación "opuesta" en ambos lados de la ecuación. Por ejemplo, en la ecuación x + 3 = 0, dado que vemos un "+ 3" al lado de la x, colocaremos un "- 3" en ambos lados. El "+ 3" y el "- 3", aislando x y el "-3" en el otro lado del signo igual, de esta forma: x = -3.
- En general, la suma y la resta son como "opuestos", así que efectúa una de ellas para deshacerte de la otra. Lee lo siguiente:
  
  Para deshacerte de la suma, resta. Ejemplo: x + 9 = 3 → x = 3 - 9
  
  Para deshacerte de la resta, suma. Ejemplo: x - 4 = 20 → x = 20 + 4
3
Cancela la multiplicación con la división (y viceversa). La multiplicación y la división son operaciones un poco más difíciles con las que trabajar, pero tienen la misma relación de "oposición". Si ves un "× 3" en un lado, lo cancelarás al dividir ambos lados entre 3 y así sucesivamente.
- Con la multiplicación y la división, debes efectuar la operación opuesta en todos los números del otro lado del signo igual, incluso si hay más de uno. Lee lo siguiente:
  
  Para deshacerte de la multiplicación, divide. Ejemplo: 6x = 14 + 2→ x = (14 + 2)/6
  
  Para deshacerte de la división, multiplica. Ejemplo: x/5 = 25 → x = 25 × 5
4
Cancela los exponentes al sacar la raíz (y viceversa). Los exponentes son un tema previo al álgebra bastante avanzado; si no sabes cómo resolverlos, lee el artículo "Cómo resolver exponentes" para obtener más información. Lo "opuesto" de un exponente es la raíz que tiene el mismo número que él. Por ejemplo, el opuesto del exponente² es una raíz cuadrada (√), el del exponente ³ es la raíz cúbica (³√) y así sucesivamente.
- Puede ser un poco confuso, pero en estos casos, si tienes un exponente, saca la raíz en ambos lados. Por el otro lado, si tienes una raíz, toma el exponente de ambos lados. Lee lo siguiente:
  
  Para deshacerte de los exponentes, saca la raíz. Ejemplo: x² = 49 → x = √49
  
  Para deshacerte de la raíz, toma el exponente. Ejemplo: √x = 12 → x = 12²

Parte 4

Parte 4 de 5:
Mejorar tus habilidades para el álgebra

1
Emplea imágenes para que los problemas se vean más claros. Si tienes dificultades para visualizar un problema de álgebra, trata de utilizar diagramas o imágenes para ilustrar la ecuación. Incluso puedes tratar de emplear un grupo de objetos físicos (como bloques o monedas) en caso de que tengas algunos a la mano.
- Por ejemplo, resolvamos la ecuación x + 2 = 3 utilizando cajas (☐)
  
  x +2 = 3
  
  ☒+☐☐ =☐☐☐
  
  En este punto, restaremos 2 de ambos lados quitando 2 cajas (☐☐) en ambos lados:
  
  ☒+☐☐-☐☐ =☐☐☐-☐☐
  
  ☒=☐, o x = 1
- Como otro ejemplo, probemos 2x = 4
  
  ☒☒ =☐☐☐☐
  
  En este punto, dividiremos ambos lados entre dos separando las cajas en cada lado en dos grupos:
  
  ☒|☒ =☐☐|☐☐
  
  ☒ = ☐☐ o x = 2
2
Emplea "marcas de sentido común" (sobre todo para problemas con palabras). Al convertir un problema con palabras en álgebra, revisa tu fórmula reemplazando valores simples para la variable. ¿La ecuación tiene sentido cuando x=0? ¿Cuando x=1? ¿Cuando x = -1? Es fácil cometer errores simples al escribir p=d/6 cuando lo que quieres decir es p=d/6, pero serán fáciles de detectar si haces una revisión rápida de tu trabajo antes de proseguir.
- Por ejemplo, supongamos que nos dicen que una cancha de fútbol mide 27,5 m (30 yardas) más de largo que de ancho. Utilizamos la ecuación l = w + 27,5 para representar el problema. Podremos evaluar si esta ecuación es válida reemplazando valores simples para w. Por ejemplo, si la cancha de fútbol es w = 9 m (10 yardas) de ancho, será 9 + 27,5 = 36,5 m (40 yardas) de largo. Si tiene 27,5 m (30 yardas) de ancho, será 27,5 + 27,5 = 55 m (60 yardas) de largo, etc. Esto tiene sentido: esperaríamos que la cancha fuera más larga que ancha, así que esta ecuación es lógica.
3
Ten en cuenta que en álgebra las respuestas obtenidas no siempre son números integrales. Las respuestas obtenidas en álgebra y en otras formas avanzadas de matemáticas no siempre son números enteros y sencillos. Con frecuencia, pueden ser decimales, fracciones o números irracionales. Puedes utilizar una calculadora para resolver estos problemas complicados, pero ten en cuenta que tu profesor podría pedirte que des la respuesta en su forma exacta, y no en forma decimal.
- Por ejemplo, supongamos que reducimos una ecuación algebraica a x = 1250⁷. Si escribimos 1250⁷ en una calculadora, obtendremos una lista larga de decimales (además, dado que la pantalla de la calculadora no es tan grande, no podrá mostrar la respuesta correcta). En este caso, podemos representar nuestra respuesta con un número tan simple como 1250⁷ o simplificarla escribiéndola en una notación científica.
4
Cuando creas haber dominado el álgebra básica, prueba con la factorización. Una de las habilidades más complicadas en álgebra es la factorización, la cual es una especie de atajo para reducir a las ecuaciones complejas a formas más simples. La factorización es un tema de álgebra semi avanzado, así que considera la posibilidad de consultar el artículo indicado líneas arriba en caso de que tengas problemas para dominarlo. Los siguientes son algunos ejemplos rápidos para factorizar ecuaciones:
- Las ecuaciones que tienen la forma ax + ba se factorizan a a(x + b). Ejemplo: 2x + 4 = 2(x + 2)
- Las ecuaciones que tienen la forma ax² + bx se factorizan a cx((a/c)x + (b/c)) donde c es el número más grande que se divide entre a y b equitativamente. Ejemplo: 3y² + 12y = 3y(y + 4)
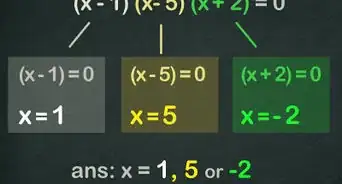
- Las ecuaciones que tienen la forma x² + bx + c se factorizan a (x + y)(x + z) donde y × z = c y yx + zx = bx. Ejemplo: x² + 4x + 3 = (x + 3)(x + 1).
5
¡Practica, practica y practica! Para progresar en álgebra (y en cualquier otra clase de matemáticas), es necesario mucho esfuerzo y repetición. No te preocupes: solo presta atención en clase, haz todas tus tareas y pídele ayuda tu profesor o a otros estudiantes siempre que lo necesites, y así el álgebra será algo muy sencillo para ti.
6
Pídele ayuda tu profesor para que te ayude a entender los temas difíciles de álgebra. Si tienes dificultades para entender álgebra, no te preocupes: no es necesario que lo aprendas por tu cuenta. Tu profesor es la primera persona a quien debes acudir con preguntas. Después de clase, pídele cortésmente que te ayude. Los buenos profesores generalmente estarán dispuestos a explicarte el tema del día en una clase después de la escuela e incluso pueden darte algunos materiales de práctica extra.
- Si, por alguna razón, tu profesor no puede ayudarte, pregúntale acerca de algunas alternativas de tutoría que haya en tu escuela. Muchas escuelas cuentan con algún tipo de programa extracurricular que pueda ayudarte a obtener el tiempo y la atención adicional que necesitas para dominar álgebra. Recuerda que utilizar la ayuda gratuita disponible no es algo por lo que debas sentir vergüenza, ¡sino que es una señal de que eres lo suficientemente inteligente como para resolver tu problema!

Parte 5

Parte 5 de 5:
Explorar los temas de nivel intermedio

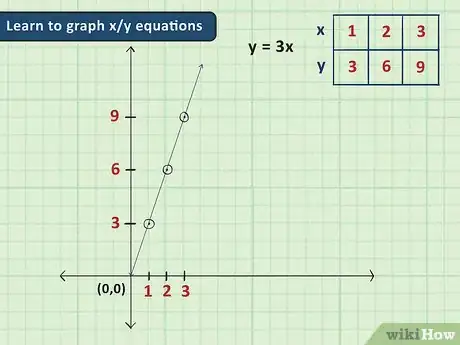
1
Aprende las ecuaciones gráficas x/y. Los gráficos pueden ser herramientas valiosas en álgebra, puesto que te permiten mostrar las ideas para las que normalmente necesitarías números en imágenes fáciles de entender. Por lo general, en el álgebra básica, los problemas de gráficos están restringidos a ecuaciones con dos variables (generalmente x e y) y se realizan en un gráfico simple en 2D con un eje x y uno y. Con estas ecuaciones, todo lo que necesitas hacer es darle un valor a x y resolver y (o viceversa) para obtener dos números que correspondan a un punto en el gráfico.
- Por ejemplo, en la ecuación y = 3x, si le damos el valor de 2 a x, obtendremos y = 6. Esto significa que el punto (2,6) (2 espacios a la derecha del centro y 6 espacios por encima del centro) es parte del gráfico de la ecuación.
- Las ecuaciones con la forma y = mx + b donde m y b son números) son especialmente comunes en el álgebra básica. Estas ecuaciones siempre tienen una pendiente de m y cruzan el eje y en y = b.
2
Aprende a resolver desigualdades. ¿Qué haces cuando tu ecuación no emplea un signo igual? Pues nada muy diferente de lo que harías normalmente. En el caso de las desigualdades, las cuales utilizan los signos como > ("mayor que") y < ("menor que") se resuelven de manera normal. Terminarás con una respuesta mayor o menor que la variable.
- Por ejemplo, con la ecuación 3 > 5x - 2, la resolveríamos de la misma manera como si fuera una normal:
  
  3 > 5x - 2
  
  5 > 5x
  
  1 > x, o x < 1
- Esto significa que todos los números menores de 1 sirven para x. En otras palabras, x puede ser 0, -1, -2 y así sucesivamente. Si relacionamos estos números en la ecuación para x, siempre obtendremos una respuesta menor que 1.
3
Resuelve las ecuaciones cuadráticas. Un tema algebraico con lo que muchos principiantes tienen dificultades para resolver son las ecuaciones cuadráticas. Estas ecuaciones tienen la forma ax² + bx + c = 0, donde a, b, y c son números (excepto que a no puede ser 0). Estas ecuaciones se resuelven con la fórmula x = -b +/- √(b² - 4ac)/2a. Ten cuidado que el signo +/- significa que necesitas hallar las respuestas para la suma y la resta, de modo que tendrás dos respuestas para estos tipos de problemas.
- Como ejemplo, resolvamos la fórmula cuadrática 3x² + 2x -1 = 0.
  
  x = [-b +/- √(b² - 4ac)]/2a
  
  x = [-2 +/- √(2² - 4(3)(-1))]/2(3)
  
  x = [-2 +/- √(4 - (-12))]/6
  
  x = [-2 +/- √(16)]/6
  
  x = [-2 +/- 4]/6
  
  x = -1 and 1/3
4
Experimenta con el sistema de ecuaciones. Resolver más de una ecuación al mismo tiempo puede parecer algo muy complicado, pero cuando trabajas con ecuaciones algebraicas simples no lo es tanto. Con frecuencia, los profesores de álgebra utilizan un método gráfico para resolver estos problemas. Cuando trabajas con un sistema de dos ecuaciones, las soluciones son los puntos en un gráfico en donde las líneas para ambas ecuaciones se cruzan.
- Por ejemplo, supongamos que trabajamos con un sistema que contenga las ecuaciones y = 3x - 2 e y = -x - 6. Si dibujamos estas dos líneas en un gráfico, obtendremos una línea que sube en un ángulo empinado y una que baja en un ángulo leve. Dado que estas líneas se cruzan en el punto (-1,-5), esta es una solución para el sistema.^{[1]
  X
  Fuente de investigación}
- Si queremos verificar nuestro problema, podemos hacerlo reemplazando nuestra respuesta en la ecuación del sistema. Una respuesta correcta debe "funcionar" para ambos.
  
  y = 3x - 2
  
  -5 = 3(-1) - 2
  
  -5 = -3 - 2
  
  -5 = -5
  
  y = -x - 6
  
  -5 = -(-1) - 6
  
  -5 = 1 - 6
  
  -5 = -5
- Ambas ecuaciones se cumplen, ¡así que nuestra respuesta es correcta!

Consejos

Hay miles de recursos para aprender álgebra en Internet. Por ejemplo, una simple búsqueda como "ayuda con álgebra" puede dar lugar a docenas de resultados excelentes. También puedes buscar más artículos de matemáticas de wikiHow. Existe una enorme cantidad de información en la web, ¡así que empieza a explorar ya mismo!
Un excelente sitio para principiantes en álgebra es: khanacademy.com. Este sitio gratuito ofrece miles de lecciones fáciles de seguir sobre una variedad enorme de temas, entre ellos el álgebra. Existen videos para todo tipo de temas, desde los temas más básicos hasta los más avanzados de nivel universitario, ¡así que no tengas miedo de sumergirte en el material de Khan Academy y comienza a utilizar toda la ayuda que tenga para ofrecerte!
No olvides de que tus mejores recursos cuando quieres aprender álgebra pueden ser las personas con las que ya te sientas cómodo. Habla con amigos o compañeros de estudios que tengan clases contigo en caso de que necesites ayuda adicional para entender la última lección.
No esperes hasta el último minuto para pedir ayuda si la necesitas.