Este artículo fue coescrito por David Jia. David Jia es tutor académico y el fundador de LA Math Tutoring, una empresa de tutoría privada con sede en Los Ángeles, California. Con más de 10 años de experiencia en enseñanza, David trabaja con estudiantes de todas las edades y grados en diversas materias, así como en asesoría para postulaciones universitarias y preparación para pruebas como el SAT, ACT, ISEE y más. Luego de obtener una calificación perfecta de 800 en matemáticas y 690 en inglés en el SAT, David recibió la beca Dickinson de la Universidad de Miami, donde se graduó con una licenciatura en Administración de Empresas. Asimismo, ha trabajado como instructor para videos en línea para empresas de libros de texto como Larson Texts, Big Ideas Learning y Big Ideas Math.
En este artículo, hay 8 referencias citadas, que se pueden ver en la parte inferior de la página.
Este artículo ha sido visto 33 807 veces.
Un polinomio es una expresión creada para sumar y restar términos. Un término puede estar constituido por constantes, coeficientes y variables. Cuando se resuelven polinomios, usualmente se trata de averiguar los valores de cada x, y=0. Los polinomios de grados inferiores tendrán cero, una o dos soluciones reales, dependiendo de si son polinomios lineales o polinomios cuadráticos. Estos tipos de polinomios pueden resolverse fácilmente usando álgebra básica y métodos de factorización. Si quieres saber cómo resolver polinomios de grado superior, lee el artículo Cómo resolver polinomios de grados superiores.
Pasos
Método 1
Método 1 de 2:Resolver un polinomio lineal
-
1Determina si tienes un polinomio lineal. Un polinomio lineal es un polinomio del primer grado.[1] Esto significa que ninguna variable tendrá un exponente más alto que uno. Ya que este es un polinomio de primer grado, tendrá exactamente una raíz real o solución.[2]
- Por ejemplo, es un polinomio lineal, porque la variable no tiene exponente (lo que es igual a un exponente de 1).
-
2Iguala la ecuación a cero. Este es un paso necesario para resolver todos los polinomios.
- Por ejemplo,
-
3Despeja la variable del término. Para hacerlo, suma o resta la constante de ambos lados de la ecuación. Una constante es un término sin una variable.[3]
- Por ejemplo, para despejar la variable en , debes restar de ambos lados de la ecuación:
- Por ejemplo, para despejar la variable en , debes restar de ambos lados de la ecuación:
-
4Resuelve la variable. Por lo general, deberás dividir cada lado de la ecuación entre el coeficiente. Esto le dará la raíz o solución a su polinomio.
- Por ejemplo, para resolver in , deberás dividir cada lado de la ecuación entre :
Por lo tanto, es la solución a is .
- Por ejemplo, para resolver in , deberás dividir cada lado de la ecuación entre :
Método 2
Método 2 de 2:Resolver un polinomio cuadrático
-
1Determina si tienes un polinomio cuadrático. Un polinomio cuadrático es un polinomio de segundo grado.[4] Esto significa que ninguna variable tendrá un exponente más alto que dos. Dado que este es un polinomio de segundo grado, tendrá dos raíces reales o soluciones.[5]
- Por ejemplo, es un polinomio cuadrático, porque la variable tiene un exponente de .
-
2Asegúrate de que el polinomio esté escrito en orden de grado. Esto significa que el término con el exponente de se enuncia primero, seguido del término de primer grado, seguido de la constante.[6]
- Por ejemplo, debes reescribir como .
-
3Iguala la ecuación a cero. Este es un paso necesario para resolver todos los polinomios.
- Por ejemplo, .
-
4Reescribe la expresión como una expresión de cuatro términos. Para hacerlo, separa el término de primer grado (el término ). Aquí deberás buscar dos números cuya suma sea igual al coeficiente de primer grado y cuyo producto sea igual a la constante.[7]
- Por ejemplo, para el polinomio cuadrático , necesitas encontrar dos números ( y ), donde , y .
- Como tienes , sabemos que uno de los números será negativo.
- Deberás ver que y . En consecuencia, debes separar dentro de y reescribir el polinomio cuadrático: .
-
5Factoriza por agrupación. Para hacer esto, factoriza un término común a los dos primeros términos en el polinomio.[8]
- Por ejemplo, los primeros dos términos en el polinomio son . Un término común a los dos es . Así, el grupo factorizado es .
-
6Factoriza el segundo grupo. Para hacerlo, factoriza un término común a los dos segundos términos en el polinomio.
- Por ejemplo, los dos segundos términos en el polinomio son . Un término común a los dos es . Entonces, el grupo factorizado es .
-
7Reescribe el polinomio como dos binomios. Un binomio es una expresión de dos términos. Ya tienes un binomio, que es la expresión entre paréntesis para cada grupo. Esta expresión debe ser la misma para cada grupo. El segundo binomio se crea al combinar los dos términos que fueron factorizados de cada grupo.
- Por ejemplo, después de factorizar por agrupación, esto se convierte en .
- El primer binomio es .
- El segundo binomio es .
- Por lo tanto, el polinomio cuadrático original se puede escribir como la expresión factorizada .
-
8Halla la primera raíz o solución. Para hacerlo, resuelve en el primer binomio.[9]
- Por ejemplo, para encontrar la primera raíz para , primero debes llevar la expresión inicial del binomio a y resolver . En consecuencia:
Así que, la primera raíz del polinomio cuadrático es .
- Por ejemplo, para encontrar la primera raíz para , primero debes llevar la expresión inicial del binomio a y resolver . En consecuencia:
-
9Halla la segunda raíz o solución. Para hacerlo, resuelve en el segundo binomio.[10]
- Por ejemplo, para encontrar la segunda raíz para , debes llevar la segunda expresión del binomio a y resolver . Como resultado :
De esta manera, la segunda raíz del polinomio cuadrático es .
- Por ejemplo, para encontrar la segunda raíz para , debes llevar la segunda expresión del binomio a y resolver . Como resultado :
Consejos
- No te preocupes si obtienes diferentes variables, como t, o si ves una ecuación llevada a f(x) en vez de 0. Si la pregunta requiere raíces, ceros o factores, simplemente trátala como cualquier otro problema.
- Recuerda el orden de las operaciones mientras trabajas. Primero trabaja resuelve el paréntesis, luego haz la multiplicación y división, y finalmente suma y resta.[11]
Referencias
- ↑ http://www.mathwords.com/l/linear_polynomial.htm
- ↑ https://www.math.utah.edu/~wortman/1050-text-calp.pdf
- ↑ http://www.mathwords.com/c/constant.htm
- ↑ http://www.mathwords.com/q/quadratic_polynomial.htm
- ↑ http://www.themathpage.com/aprecalc/quadratic-equation.htm#double
- ↑ http://www.mesacc.edu/~scotz47781/mat120/notes/factoring/trinomials/a_is_not_1/trinomials_a_is_not_1.html
- ↑ https://www.khanacademy.org/math/algebra/quadratics/solving-quadratic-equations-by-factoring/v/example-1-solving-a-quadratic-equation-by-factoring
- ↑ http://www.mesacc.edu/~scotz47781/mat120/notes/factoring/trinomials/a_is_not_1/trinomials_a_is_not_1.html
- ↑ https://www.khanacademy.org/math/algebra/quadratics/solving-quadratic-equations-by-factoring/v/example-1-solving-a-quadratic-equation-by-factoring




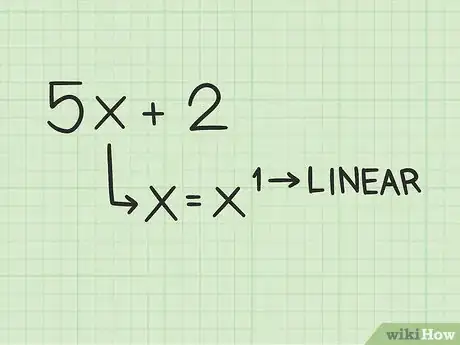


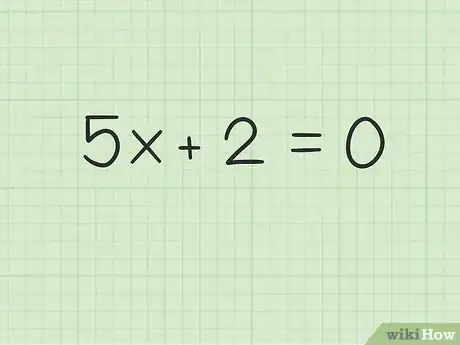

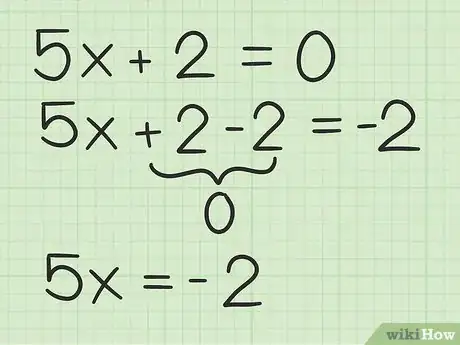



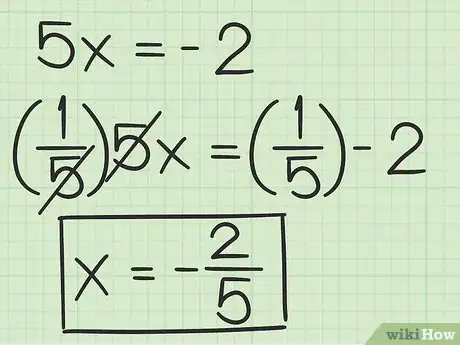



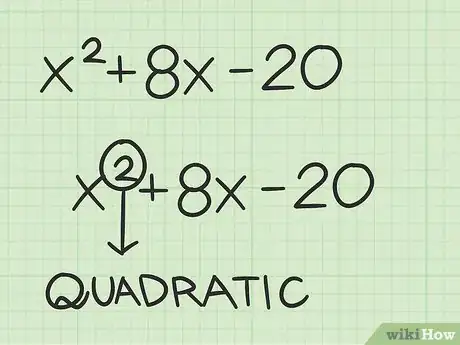

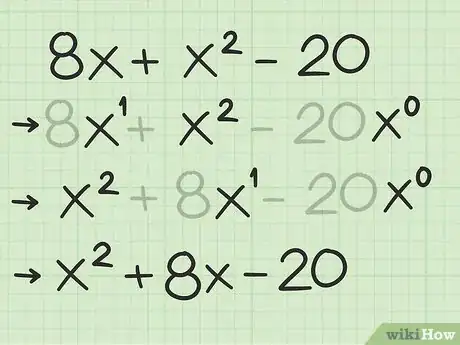

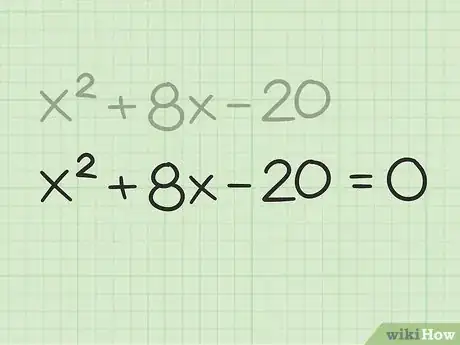

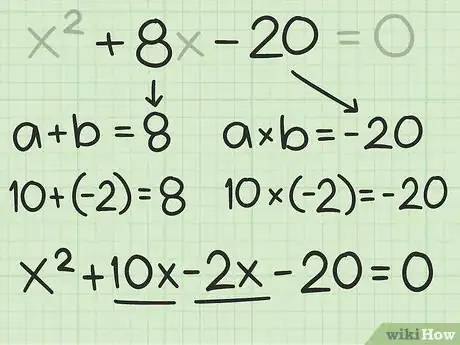










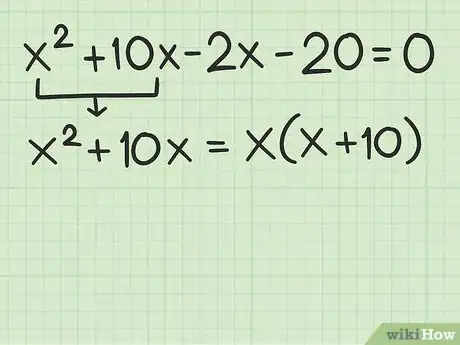


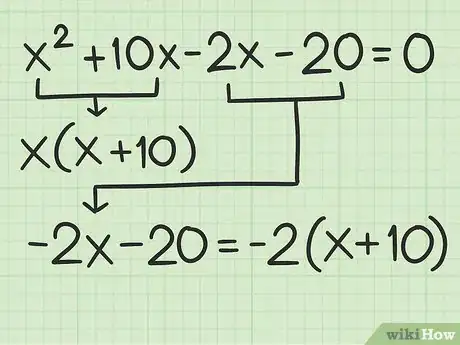



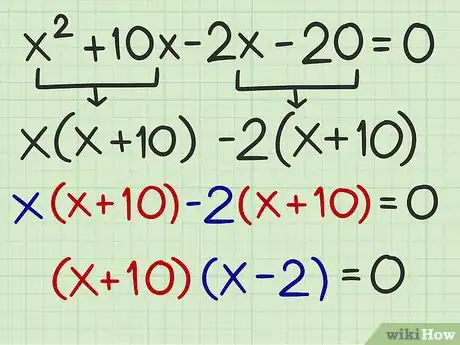




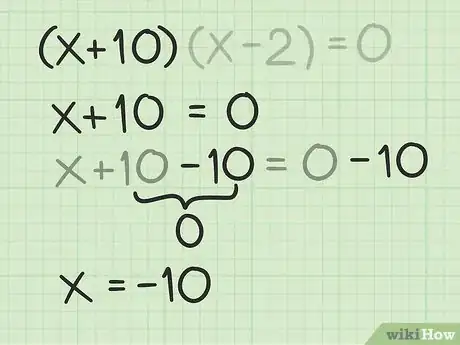





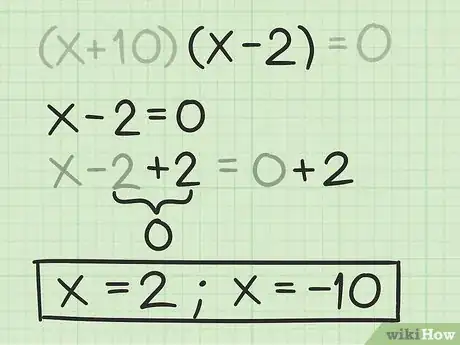







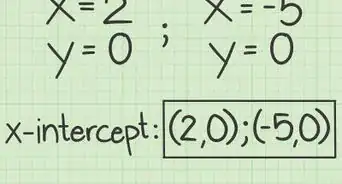
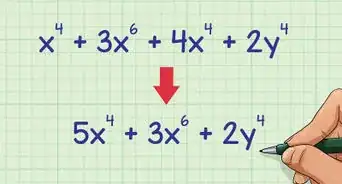
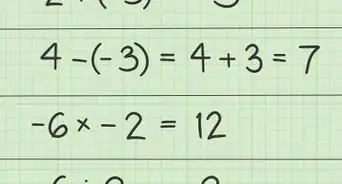
-Step-31-Version-2.webp)