Nuestro equipo de editores e investigadores capacitados han sido autores de este artículo y lo han validado por su precisión y amplitud.
wikiHow's Content Management Team revisa cuidadosamente el trabajo de nuestro personal editorial para asegurar que cada artículo cumpla con nuestros altos estándares de calidad.
Este artículo ha sido visto 184 069 veces.
Al empezar a estudiar álgebra, verás ecuaciones que tengan una variable a un lado pero, más adelante, a menudo también verás ecuaciones con variables en ambos lados. Lo más importante que debes recordar al resolver estas ecuaciones es que, independientemente de lo que hagas en un lado de la ecuación, debes hacer lo mismo en el otro lado. Usando esta regla, es fácil mover las variables para aislarlas y usar las operaciones básicas para encontrar su valor.
Pasos
Método 1
Método 1 de 3:Resolver ecuaciones con una variable en ambos lados
-
1Si es necesario, aplica la propiedad distributiva. Según la propiedad distributiva, .[1] Esta regla te permite eliminar los paréntesis multiplicando cada término entre paréntesis por el número que esté afuera.[2]
- Por ejemplo, si la ecuación es , usa la propiedad distributiva para multiplicar los términos entre paréntesis por el número que está afuera:
- Por ejemplo, si la ecuación es , usa la propiedad distributiva para multiplicar los términos entre paréntesis por el número que está afuera:
-
2Cancela la variable en un lado de la ecuación. Para cancelar la variable, realiza la operación contraria a la que figura en la ecuación. Por ejemplo, si en la ecuación el término se resta, cancélalo sumándolo. Si el término se suma, restalo para cancelarlo. Por lo general, es más fácil cancelar la variable con el coeficiente más bajo.[3]
- Por ejemplo, en la ecuación , cancela el término sumando :
- Por ejemplo, en la ecuación , cancela el término sumando :
-
3Mantén la ecuación balanceada. Todo lo que hagas en un lado de la ecuación debes repetirlo en el otro. Entonces, si sumas o restas para cancelar la variable en un lado de la ecuación, también debes sumar o restar en el otro lado.[4]
- Por ejemplo, si sumaste en un lado de la ecuación para cancelar la variable, también debes sumar en el otro lado de la ecuación:
- Por ejemplo, si sumaste en un lado de la ecuación para cancelar la variable, también debes sumar en el otro lado de la ecuación:
-
4Combina los términos similares para simplificar la ecuación. Ahora, la variable debe estar en un solo lado de la ecuación.
- Por ejemplo :
- Por ejemplo :
-
5Si es necesario, pasa todas las constantes a un mismo lado de la ecuación. El término con la variable debe estar en un lado y la constante en el otro. Para mover la constante a uno de los lados, suma o resta la misma cantidad a cada lado de la ecuación para cancelar el término en uno de los lados.[5]
- Por ejemplo, para cancelar la constante del lado de la variable, resta 8 a ambos lados de la ecuación:
- Por ejemplo, para cancelar la constante del lado de la variable, resta 8 a ambos lados de la ecuación:
-
6Cancela el coeficiente de la variable. Para hacerlo, realiza la operación contraria a la que figure en la ecuación. Por lo general, esto significa dividir para cancelar un coeficiente que esté multiplicado por una variable.[6] Recuerda que todo lo que hagas en un lado de la ecuación debes repetirlo en el otro lado.
- Por ejemplo, para cancelar el coeficiente 12 de la ecuación, dividirías cada lado de la ecuación entre 12:
- Por ejemplo, para cancelar el coeficiente 12 de la ecuación, dividirías cada lado de la ecuación entre 12:
-
7Revisa tu trabajo. Para asegurarte de que la respuesta sea correcta, reemplaza tu solución en la ecuación original. Si ambos lados son iguales, la respuesta es correcta.
- Por ejemplo, si , reemplaza 1 por la variable en la ecuación y calcula:
Anuncio - Por ejemplo, si , reemplaza 1 por la variable en la ecuación y calcula:
Método 2
Método 2 de 3:Resolver sistemas de ecuaciones con dos variables
-
1Aísla una variable en una ecuación. Esto podría ya estar hecho. Si no es así, usa las reglas del álgebra para aislar la variable en un lado de la ecuación. Recuerda que todo lo que hagas en un lado de la ecuación debes repetirlo en el otro.
- Por ejemplo, en la ecuación , para aislar la variable , restarías 1 a ambos lados:
- Por ejemplo, en la ecuación , para aislar la variable , restarías 1 a ambos lados:
-
2Reemplaza el valor de la variable aislada en la otra ecuación. Asegúrate de reemplazar toda la expresión por la variable. Esto te dará una ecuación con una sola variable, lo que te permitirá encontrar ese valor.[7]
- Por ejemplo, si la primera ecuación es y determinaste que en la segunda ecuación, reemplazarías por en la primera ecuación:
- Por ejemplo, si la primera ecuación es y determinaste que en la segunda ecuación, reemplazarías por en la primera ecuación:
-
3Encuentra el valor de la variable. Para esto, pasa la variable a un lado de la ecuación y las constantes al otro lado de la ecuación. Luego, aísla la variable multiplicando o dividiendo.
- Por ejemplo:
- Por ejemplo:
-
4Encuentra el valor de la variable restante. Para esto, reemplaza en una de las ecuaciones el valor de la variable que ya tengas. Esto te dará una ecuación con una sola variable. Encuentra el valor de esta variable usando las reglas del álgebra. Puedes usar cualquiera de las ecuaciones para encontrar la variable restante.
- Por ejemplo, si encontraste que , puedes reemplazar por 6 en la segunda ecuación:
- Por ejemplo, si encontraste que , puedes reemplazar por 6 en la segunda ecuación:
-
5Revisa tu trabajo. Reemplaza los valores de ambas variables en una de las ecuaciones. Si ambos lados son iguales, las soluciones son correctas.
- Por ejemplo, si encontraste que e , reemplázalas en la ecuación original y resuelve:
Anuncio - Por ejemplo, si encontraste que e , reemplázalas en la ecuación original y resuelve:
Método 3
Método 3 de 3:Resolver problemas de ejemplo
-
1Intenta este problema usando la propiedad distributiva con una variable: .
- Usa la propiedad distributiva para eliminar el paréntesis:
- Cancela en el lado izquierdo de la ecuación restando a ambos lados:
- Aísla la variable sumando 5 a cada lado de la ecuación:
- Usa la propiedad distributiva para eliminar el paréntesis:
-
2Intenta este problema que involucra una fracción: .
- Elimina la fracción. Para esto, multiplica cada lado de la ecuación por el denominador de la fracción:
- Cancela en el lado derecho de la ecuación sumando a cada lado:
- Pasa las constantes a un mismo lado de la ecuación sumando 14 a cada lado:
- Cancela el coeficiente dividiendo cada lado de la ecuación entre 7:
- Elimina la fracción. Para esto, multiplica cada lado de la ecuación por el denominador de la fracción:
-
3Intenta resolver este sistema de ecuaciones: .
- Aísla la variable en la segunda ecuación:
- Reemplaza por en la primera ecuación:
- Usa la propiedad distributiva para eliminar el paréntesis:
- Cancela la variable en el lado izquierdo de la ecuación restando a cada lado:
- Pasa las constantes a un mismo lado restando 36 a cada lado:
- Cancela el coeficiente dividiendo cada lado entre 3:
- Encuentra el valor de reemplazando el valor de en cualquiera de las ecuaciones:
Anuncio - Aísla la variable en la segunda ecuación:
Cosas que necesitarás
- lápiz
- papel
- calculadora
Referencias
- ↑ http://www.coolmath.com/prealgebra/06-properties/05-properties-distributive-01
- ↑ http://www.virtualnerd.com/algebra-1/linear-equations-solve/variables-both-sides-equations/variables-both-sides-solution/variables-grouping-symbols-both-sides
- ↑ http://www.regentsprep.org/regents/math/algebra/ae2/lsolveq.htm
- ↑ http://www.regentsprep.org/regents/math/algebra/ae2/lsolveq.htm
- ↑ http://www.algebralab.org/studyaids/studyaid.aspx?file=Algebra1_3-3.xml
- ↑ http://www.algebralab.org/studyaids/studyaid.aspx?file=Algebra1_3-3.xml
- ↑ http://www.virtualnerd.com/pre-algebra/linear-functions-graphing/system-of-equations/solving-systems-equations/two-equations-two-variables-substitution




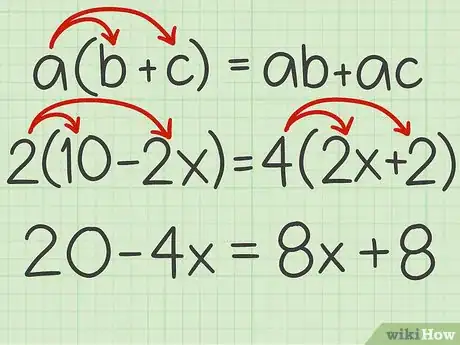



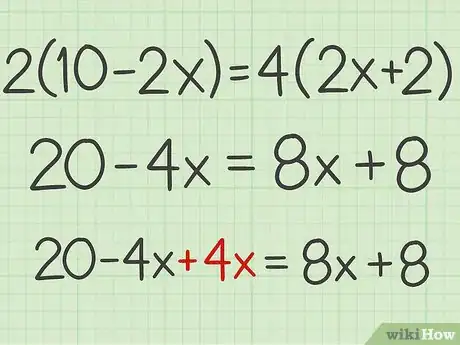



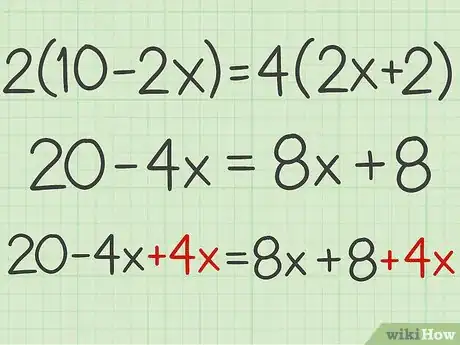

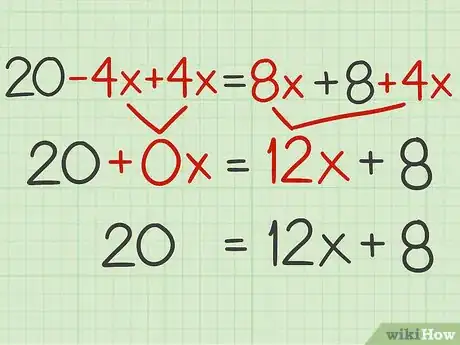

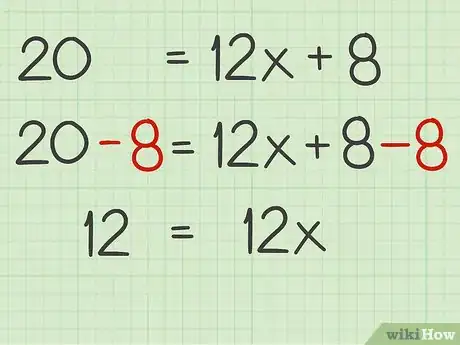



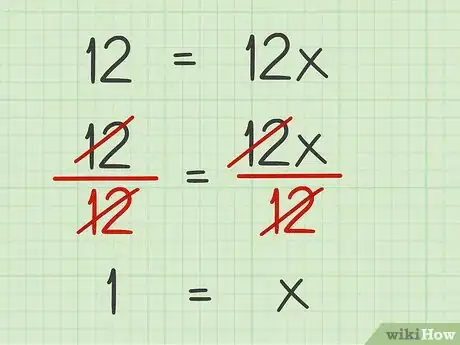


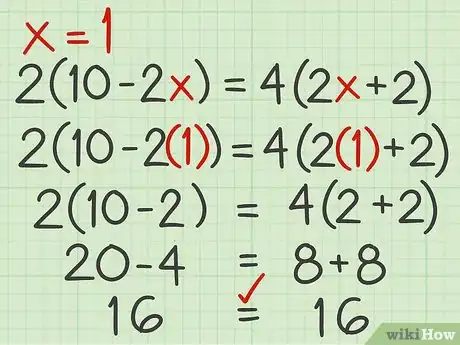




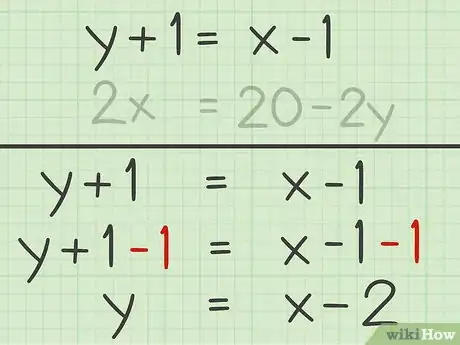




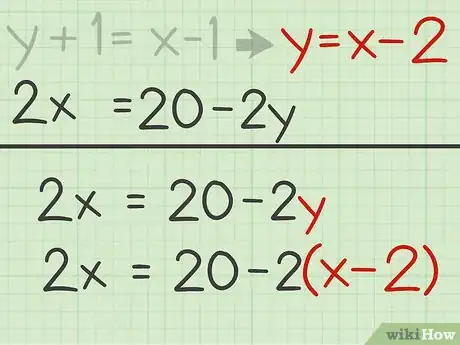



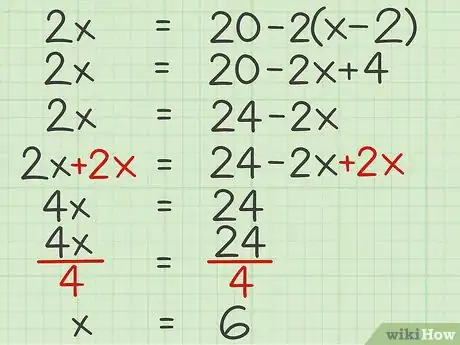






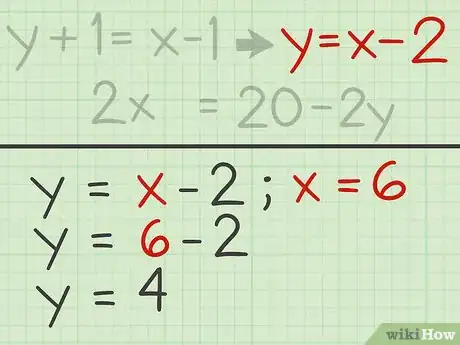



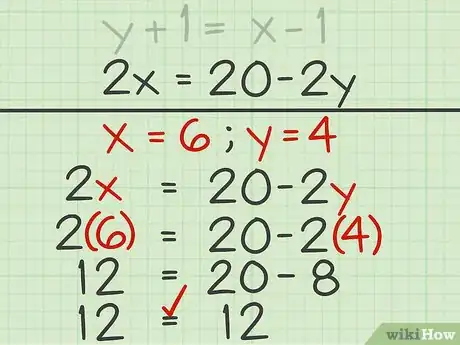



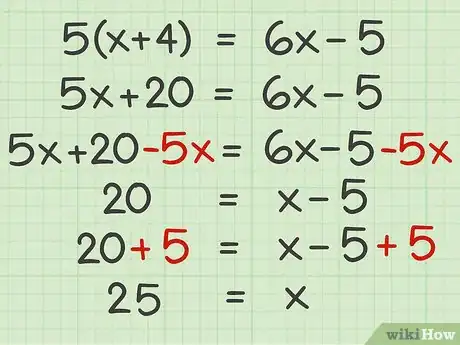












































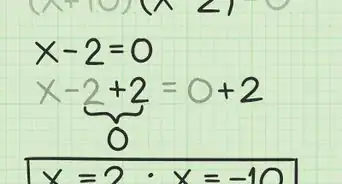
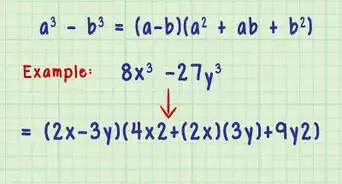
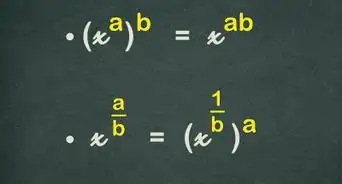
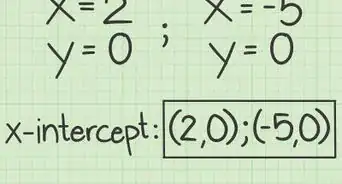
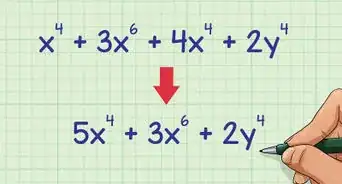
-Step-31-Version-2.webp)




wikiHow's Content Management Team revisa cuidadosamente el trabajo de nuestro personal editorial para asegurar que cada artículo cumpla con nuestros altos estándares de calidad. Este artículo ha sido visto 184 069 veces.