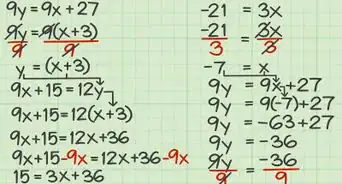Este artículo fue coescrito por Daron Cam. Daron Cam es tutor académico y fundador de Bay Area Tutors, Inc., un servicio de tutoría con sede en el Área de la Bahía de San Francisco que ofrece tutoría en matemáticas, ciencias y desarrollo de confianza académica en general. Daron cuenta con más de ocho años de experiencia en la enseñanza de matemáticas en aulas, así como más de nueve en tutoría individual. Enseña todos los niveles de matemáticas, incluidos cálculo, preálgebra, álgebra I, geometría y preparación de matemáticas SAT/ACT. Tiene un bachiller en la Universidad de California, Berkeley, así como una credencial en enseñanza de matemáticas en St. Mary’s College.
En este artículo, hay 8 referencias citadas, que se pueden ver en la parte inferior de la página.
Este artículo ha sido visto 50 737 veces.
Entender el álgebra puede parecer difícil al principio; sin embargo, si desarrollas un conocimiento básico sólido de operaciones matemáticas para principiantes y aprendes un poco del “lenguaje” del álgebra, podrás entenderlo mucho más fácilmente. Las bases para resolver problemas de álgebra implican realizar operaciones simples en pequeños pasos que “cancelen” el problema original. Realizar estos pasos cuidadosa y ordenadamente te conducirá a la solución.
Pasos
Parte 1
Parte 1 de 5:Saber cuáles son tus objetivos en álgebra
-
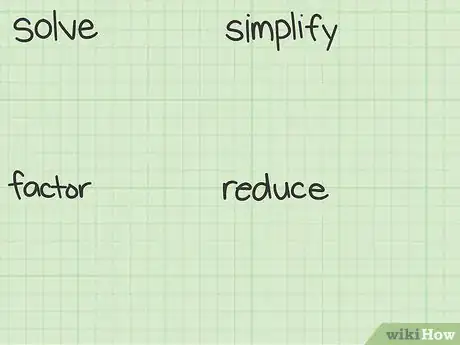
1Lee las instrucciones del problema cuidadosamente. Cuando tengas uno o más problemas de álgebra, debes leer las instrucciones cuidadosamente. Busca las palabras clave en las instrucciones, como “resolver”, “simplificar”, “factorizar” o “reducir”. Estas son algunas de las instrucciones más comunes (aunque hay otras que aprenderás). Muchas personas tienen dificultades porque tratan de “resolver” un problema cuando lo único que deben hacer es “simplificarlo”.[1]
-
2Realiza las operaciones que se indican. Cuando leas las instrucciones del problema, debes identificar las palabras clave y luego realizar esas operaciones. Muchas personas se frustran con el álgebra cuando tratan de hacer algo que realmente no es parte del problema previsto. Las operaciones básicas que se te pedirán son las siguientes:[2]
- Resolver. Tendrás que reducir el problema a una solución numérica real, como “x=4”. Debes encontrar un valor para la variable que te permita resolver el problema.
- Simplificar. Debes manipular el problema para convertirlo en una forma más simple, pero no debes terminar con lo que puedas considerar “una respuesta”. Es muy probable que no obtengas un solo valor numérico para la variable.
- Factorizar. Esta operación es similar a “simplificar” y generalmente se usa con fracciones o polinomios complejos. Debes encontrar una forma de convertir el problema en términos más pequeños. Por ejemplo, así como el número 12 se puede descomponer en los factores 3x4, puedes factorizar un polinomio algebraico.
- Por ejemplo, una expresión simple como se puede descomponer en los factores y .
- Por ejemplo, la expresión se puede factorizar en los términos y .
- Reducir. Por lo general, “reducir” un problema implica una combinación de factorización y de simplificación. Debes descomponer los términos de un numerador y de un denominador en sus factores. Luego, debes buscar los factores comunes en la parte superior e inferior, y cancelarlos. Lo que queda es la forma “reducida” del problema original. Por ejemplo, reduce la expresión de la siguiente manera:
- 1. Factoriza el numerador y el denominador:
- 2. Busca términos comunes. Tanto el numerador como el denominador tienen factores 2 y x.
- 3. Elimina los términos comunes:
- 4. Copia lo que queda:
-
3Aprende la diferencia entre “expresión” y “ecuación”. En álgebra, la diferencia entre una “expresión” y una “ecuación” es muy importante. Una expresión es cualquier grupo de números y de variables en conjunto. Algunos ejemplos de expresiones son , y . Todo lo que puedes hacer con una expresión es simplificarla o factorizarla. Por otro lado, una ecuación contiene un signo =. Puedes simplificar o factorizar las ecuaciones, pero también puedes resolverlas para obtener una respuesta final. Es importante hallar la diferencia.[3]
- Si tienes una expresión, como , no puedes encontrar nunca una sola “respuesta” o “solución”. Puedes averiguar si , entonces la expresión tendrá un valor de 4 y si , entonces la expresión tendrá un valor de , que es 16. No obstante, no puedes obtener una sola “respuesta”.
Parte 2
Parte 2 de 5:Aplicar el orden de las operaciones
-
1Aprende el PEMDAS. En álgebra, los pasos que debes tomar se dan en un orden lógico, lo cual se llama el “orden de las operaciones”. A menudo, esto se simplifica mediante el recurso mnemotécnico “PEMDAS”. Las letras de PEMDAS te ayudarán a saber el orden en que debes realizar las operaciones. Estas letras significan lo siguiente:[4]
- paréntesis
- exponentes
- multiplicación
- división
- adición (suma)
- sustracción (resta)
-
2Realiza primero las operaciones que están dentro del paréntesis. Cuando tengas una expresión o una ecuación que incluya términos que estén dentro de paréntesis, primero debes resolver estos. Analiza la diferencia entre y .[5]
- Sin los paréntesis, la primera expresión , se convertiría en .
- Con los paréntesis, en la expresión , primero debes resolver (3+2) para que la expresión simplificada se convierta en .
-
3Simplifica cualquier exponente que venga a continuación. Se deben resolver los exponentes como la siguiente parte de la simplificación o de la resolución de un problema. Piensa en la expresión . Sin el orden de las operaciones, no tendrías cómo saber si primero debes multiplicar y luego elevar al cuadrado el resultado, de manera que obtengas el valor 36, o si primero debes elevar 2 al cuadro y luego multiplicarlo por 3. Si usas el PEMDAS, la operación correcta sería la siguiente:[6]
- (primero eleva 2 al cuadrado)
- (este es el resultado correcto)
-
4Multiplica o divide de derecha a izquierda. M y D son las siguientes dos partes del PEMDAS y van juntas. Después de resolver todos los exponentes, debes resolver la multiplicación o la división de izquierda a derecha.[7]
- 4*2=8 y 6/3=2 (estas operaciones se pueden hacer en el mismo paso)
-
5Suma o resta de derecha a izquierda. A y S son los pasos finales del PEMDAS. Esto significa que debes realizar la adición (suma) o la sustracción (resta) de cualquier término que quede en la expresión. Puedes hacerlo en el mismo paso, moviéndote de derecha a izquierda a lo largo del problema. Piensa en la expresión .[8]
- (suma 4+2)
- (resta 6-3)
- (resta 3-1)
- (resta 2-5)
- (suma -3+1)
- Si realizas estos pasos en cualquier orden, puedes obtener un resultado distinto e incorrecto. Por ejemplo, imagina que decides hacer primero todas las sumas y luego las restas, de la siguiente manera:
- (suma 4+2 y suma 5+2)
- (resta 6-3)
- (resta 3-1)
- (resta 2-7; esto da como resultado -5, lo cual es incorrecto)
Parte 3
Parte 3 de 5:Trabajar con variables
-
1Acostúmbrate a usar símbolos además de números. En las matemáticas iniciales, únicamente se usaban números. El aprendizaje del álgebra consiste en ser capaz de resolver problemas con términos desconocidos. Estos términos desconocidos se representan con letras en los problemas. Debes acostumbrarte a tratar estas letras como números, aunque quizás no sepas aún cual sea su valor real. Algunos ejemplos comunes de variables son los siguientes:[9]
- letras (como , o )
- símbolos griegos (como , o )
- Toma en cuenta que algunos símbolos pueden parecer variables, pero que realmente son números conocidos. Por ejemplo, el símbolo griego pi (, ) representa al número 3,1415.
-
2Piensa en una variable como un parámetro de sustitución desconocido. Puedes expresar la frase “Dos veces un número” con una variable como . La variable toma el lugar de “un número” desconocido. Por lo general, tu trabajo en un problema de álgebra es encontrar el valor de la variable.[10]
- Por ejemplo, si empiezas con la ecuación , debes pensar “¿Qué número se debe sumar a 4 para obtener 9?”. La solución es 5, lo cual puede escribirse algebraicamente como .
-
3Combina variables comunes. Cuando aprendas a tratar las variables como números, podrás combinarlas o simplificarlas como lo haces con los números. Por lo general, esto se llama “combinar términos similares”.[11]
- Por ejemplo, solo significa que 2 veces la variable que se suma a 3 veces la misma variable será igual a 10. Si tienes 2 de algo y 3 de la misma cosa, puedes sumar los dos elementos. Entonces, se convertirá en 5x, de manera que el problema es y la solución es .
- Únicamente puedes sumar o restar la misma variable. Algunos problemas de álgebra pueden contener dos o más variables. En el problema , no puedes combinar los términos e porque variables distintas representan números desconocidos distintos.
Parte 4
Parte 4 de 5:Resolver problemas de álgebra con operaciones inversas
-
1Aprende el concepto de las funciones inversas. Una clave para tener éxito en el álgebra es realizar funciones inversas. La palabra “inverso” significa opuesto. Las funciones inversas son una manera de deshacer o de dilucidar un problema. Por ejemplo, si un problema determinado contiene operaciones de multiplicación, usarás la división, que es el inverso de la multiplicación, para resolver el problema.[12]
- El inverso de la suma es la resta.
- El inverso de la resta es la suma
- El inverso de la multiplicación es la división
- El inverso de la división es la multiplicación
- El inverso de un exponente es una raíz (raíz cuadrada, raíz cúbica, etc.).
-
2Concéntrate en aislar la variable. Si se te pide que “resuelvas” una ecuación, significa que debes llegar a __ y obtener un número que vaya en el espacio en blanco. Debes usar el álgebra para despejar la , de manera que esté sola a un lado del signo igual. Debes hacerlo por medio de una serie de operaciones inversas.[13]
- La regla esencial que debes recordar es que cualquier operación que hagas a un lado de la ecuación, también debes hacerla al lado opuesto. De esta manera, la ecuación se mantendrá equilibrada y seguirá siendo igual.
-
3Cancela la suma usando la resta (y viceversa). Los términos individuales en una ecuación están vinculados por una combinación de los signos más y menos. Puedes “cancelarlos” (a fin de dejar sola a la variable) realizando la función opuesta.[14]
- Por ejemplo, si empiezas con , debes tratar de despejar la . El inverso de es . Recuerda que debes hacer todo por igual a ambos lados de la ecuación. De manera que debes obtener lo siguiente:
- (resta 3 en ambos lados por igual)
- (+3 y -3 se cancelan entre sí para dar paso a la solución)
- Si empiezas con un problema de resta, debes cancelarlo con una suma de la misma manera.
- (suma 8 a ambos lados)
- (+8 y -8 se cancelan entre sí para dar paso a la solución)
- Por ejemplo, si empiezas con , debes tratar de despejar la . El inverso de es . Recuerda que debes hacer todo por igual a ambos lados de la ecuación. De manera que debes obtener lo siguiente:
-
4Cancela la multiplicación usando la división (y viceversa). De la misma manera, puedes realizar operaciones inversas en la multiplicación y en la división. El término significa . Para lograr aislar la variable tendrás que dividir. Recuerda que para una ecuación, debes dividir en ambos lados de la ecuación por igual.[15]
- Imagina que tienes el problema . Debido a que se trata de un problema de multiplicación, tendrás que resolverlo con división.
- (divide ambos lados por 3; toma en cuenta que el símbolo generalmente no se usa en el álgebra; sin embargo, debes indicar que se trata de una división escribiendo los términos como una fracción)
- (los 3 de la izquierda se cancelan entre sí para dar paso a la solución)
- Haz lo mismo para cancelar un problema de división con la multiplicación. Imagina que tienes el problema .
- (multiplica ambos lados por 4)
- (los 4 de la izquierda se cancelan entre sí para dar paso a la solución)
- Imagina que tienes el problema . Debido a que se trata de un problema de multiplicación, tendrás que resolverlo con división.
-
5Usa una combinación de suma y resta, y de multiplicación y división. A medida que los problemas se hagan más complicados, es probable que debas realizar varias operaciones para obtener una solución. Por lo general, tendrás que realizar primero la suma y la resta para aislar la variable con su coeficiente. Luego, tendrás que realizar la multiplicación y la división para hallar la solución.[16]
- (primero, resta 5 de ambos lados para aislar la x)
- (+5 y -5 se cancelan en el lado izquierdo)
- (divide ambos lados entre 3)
- (los 3 del lado izquierdo se eliminan entre sí para dar paso a la solución)
-
6Verifica tu resultado. En álgebra, casi siempre puedes averiguar si has hecho el problema correctamente verificando tu respuesta. Toma la solución que has hallado e insértala en el problema original sustituyendo a la variable. Luego, simplifica el problema y, si llegas a un enunciado verdadero, entonces la solución es correcta.
- Inténtalo con el ejemplo que acabas de resolver, . Sustituye la variable con la solución .
- (inserta el valor .)
- (simplifica la ecuación)
- (esto es verdadero, de manera que la solución es correcta)
- Inténtalo con el ejemplo que acabas de resolver, . Sustituye la variable con la solución .
Parte 5
Parte 5 de 5:Desarrollar una base sólida para el aprendizaje
-
1Aprende las operaciones matemáticas básicas. El álgebra es un sistema de manipulación de números y de operaciones que se usa para tratar de resolver problemas. Cuando aprendes álgebra, aprendes las reglas que debes seguir para resolver problemas. Sin embargo, para que el proceso sea más sencillo, debes tener una comprensión sólida de las operaciones matemáticas básicas. Debes saber la suma, la resta, la multiplicación y la división básicas y debes ser capaz de usarlas fácilmente. De manera particular, debes ser capaz de hacer lo siguiente:[17]
- Suma y resta rápidamente números de un dígito en la cabeza. Ser capaz de trabajar con números de dos dígitos es aún más útil.
- Debes conocer las tablas de multiplicación del 1 al 12.
- Debes conocer la división y los divisores de números hasta 144 (12x12).
-
2Practica las reglas de las fracciones. El álgebra usa las reglas de las fracciones tanto como cualquier otro sistema de numeración. Te debe parecer sencillo hallar denominadores comunes, sumar y restar fracciones, y multiplicar y dividir fracciones. Al aprender álgebra, podrás ampliar este conocimiento para trabajar con variables desconocidas, pero primero necesitarás una comprensión sólida de las cosas básicas.[18]
- Conoce la importancia de los números recíprocos. Debes conocer el concepto de números recíprocos. La definición corta de un número recíproco es una fracción al revés. De esta manera, el número recíproco de es y el número recíproco de es . Usa números recíprocos como una alternativa a la división, cuando el problema sea complicado. En vez de dividir un término entre una fracción, puedes multiplicarlo por su número recíproco.
-
3Aprende a usar números negativos. A menudo, usarás variables o números negativos. Debes revisar cómo sumar, restar, multiplicar y dividir números negativos antes de aprender álgebra. Aquí hay algunas reglas básicas para trabajar con números negativos.[19] También puedes leer artículos como “Cómo sumar y restar números negativos” y “Cómo dividir y multiplicar números negativos” .
- En una recta numérica, un número negativo está a la misma distancia de cero que el número positivo, pero en la dirección opuesta.
- Un negativo más un negativo también será negativo. Sumar dos números negativos da como resultado un número negativo mayor.
- Dos signos negativos juntos se cancelan entre sí. Restar un número negativo es lo mismo que sumar un número positivo.
- 4-(-3) es lo mismo que 4+3=7.
- Multiplicar o dividir dos números negativos da como resultado una respuesta positiva.
- Multiplicar o dividir un número positivo y uno negativo da como resultado una respuesta negativa.
Consejos
- Usa buenos recursos para estudiar. Asiste a clases, lee las lecturas asignadas y termina tu tarea. Entender el álgebra requiere de práctica.
- Trabaja con tu profesor. Si tienes preguntas o problemas, habla con tu profesor. Algunas personas pueden entender el álgebra muy rápido, pero otras necesitan un poco más de tiempo. Tu profesor puede tener otra manera de explicarte las cosas. En vez de rendirte, pide un poco de ayuda.
- Siempre revisa tus respuestas. Cuando termines un problema, revísalo para ver si la solución corrobora que la ecuación es correcta.
- Siguiendo con el PEMDAS, también puedes convertirlo en PCEMDAS. La “C” quiere decir corchetes. Esto puede ser útil si en donde vives los usan (en algunos lugares no los usan).
Referencias
- ↑ http://www.mathplanet.com/education/algebra-2/equations-and-inequalities/solve-equations-and-simplify-expressions
- ↑ http://www.mathplanet.com/education/algebra-2/equations-and-inequalities/solve-equations-and-simplify-expressions
- ↑ https://www.algebra.com/algebra/homework/equations/Equations.faq.question.231678.html
- ↑ http://www.coolmath.com/prealgebra/05-order-of-operations/05-order-of-operations-parenthesis-PEMDAS-01
- ↑ http://www.coolmath.com/prealgebra/05-order-of-operations/05-order-of-operations-parenthesis-PEMDAS-01
- ↑ http://www.coolmath.com/prealgebra/05-order-of-operations/05-order-of-operations-parenthesis-PEMDAS-01
- ↑ http://www.coolmath.com/prealgebra/05-order-of-operations/05-order-of-operations-parenthesis-PEMDAS-01
- ↑ http://www.coolmath.com/prealgebra/05-order-of-operations/05-order-of-operations-parenthesis-PEMDAS-01
- ↑ http://www.mathplanet.com/education/algebra-1/discovering-expressions,-equations-and-functions/expressions-and-variables
- ↑ http://www.mathplanet.com/education/algebra-1/discovering-expressions,-equations-and-functions/expressions-and-variables
- ↑ http://www.algebrahelp.com/lessons/simplifying/combiningliketerms/
- ↑ https://www.mathsisfun.com/sets/function-inverse.html
- ↑ https://www.mathsisfun.com/sets/function-inverse.html
- ↑ https://www.mathsisfun.com/sets/function-inverse.html
- ↑ https://www.mathsisfun.com/sets/function-inverse.html
- ↑ https://www.mathsisfun.com/sets/function-inverse.html
- ↑ https://www.ixl.com/promo?partner=google&campaign=1087&adGroup=Math-Specific+K-8&gclid=CMq25b_49tICFd6CswodA5gMKw
- ↑ https://www.ixl.com/promo?partner=google&campaign=1087&adGroup=Math-Specific+K-8&gclid=CMq25b_49tICFd6CswodA5gMKw
- ↑ http://www.mathleague.com/index.php/about-the-math-league/mathreference?id=85




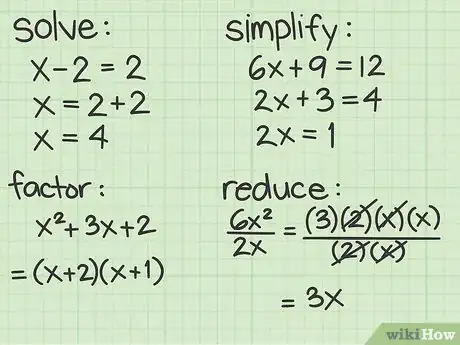









































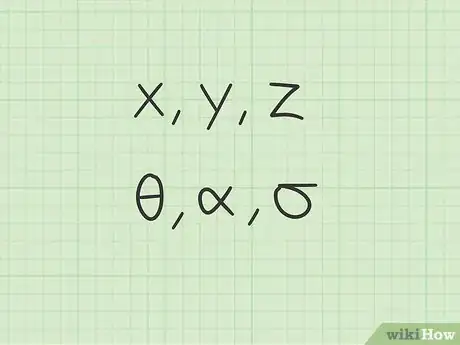






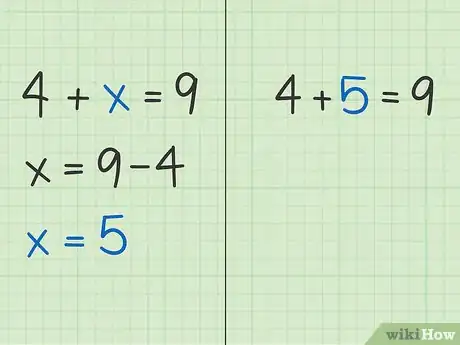



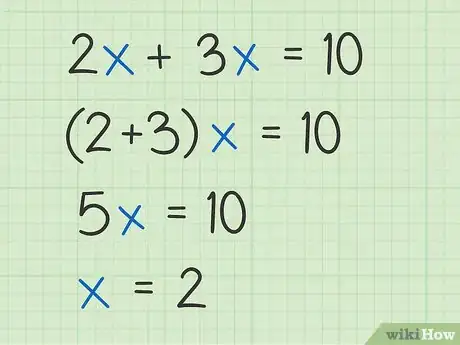



























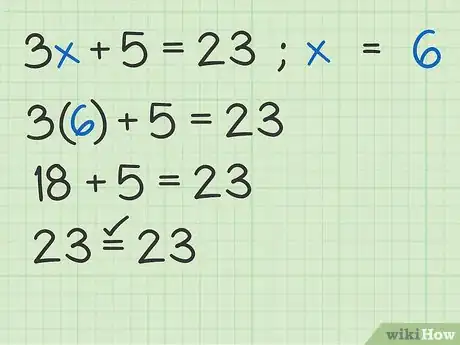








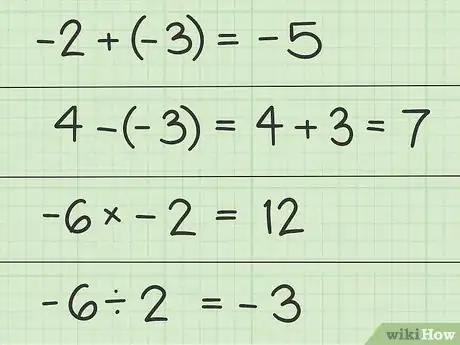




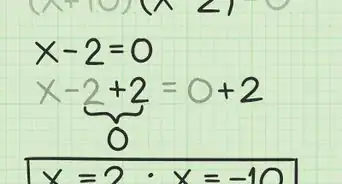
-Step-31-Version-2.webp)