X
wikiHow es un "wiki", lo que significa que muchos de nuestros artículos están escritos por varios autores. Para crear este artículo, 29 personas, algunas anónimas, han trabajado para editarlo y mejorarlo con el tiempo.
Este artículo ha sido visto 304 579 veces.
Este es un artículo acerca de cómo factorizar un polinomio de tercer grado. Vamos a explorar cómo factorizar utilizando la agrupación, así como el uso de los factores de la expresión libre.
Pasos
Parte 1
Parte 1 de 2:Factorizar con agrupación
Parte 1
-
1Agrupa el polinomio en dos secciones. Agrupar el polinomio en dos secciones te permitirá atacar cada sección por separado.[1]
- Digamos que estamos trabajando con el polinomio x3 + 3x2 - 6x - 18 = 0. Agrupémoslo en (x3 + 3x2) y (- 6x - 18).
-
2Encuentra lo que es común en cada sección.
- En cuanto a (x3 + 3x2), podemos ver que x2 es común.
- En cuanto a (- 6x - 18), podemos ver que -6 es común.
-
3Factoriza los puntos en común de los dos términos.
- Al factorizar x2 de la primera sección, obtenemos x2(x + 3).
- Al factorizar -6 de la segunda sección, obtenemos -6 (x + 3).
-
4Si cada uno de los dos términos contiene el mismo factor, se pueden combinar los factores en conjunto.[2]
- Esto nos da (x + 3)(x2 - 6).
-
5
Parte 2
Parte 2 de 2:Factorizar usando el término libre
Parte 2
-
1Vuelve a ordenar la expresión de manera que esté en forma de aX3+bX2+cX+d.[4]
- Supongamos que tenemos la ecuación: x3 - 4x2 - 7x + 10 = 0.
-
2Encuentra la totalidad de los factores de "d". La constante "d" va a ser el número que no tiene variables, como la "x", al lado de ella.
- Los factores son los números que pueden multiplicarse en conjunto para obtener otro número. En nuestro caso, los factores de 10, o "d", son: 1, 2, 5, y 10.
-
3Encuentra un factor que haga que el polinomio sea igual a cero. Queremos determinar qué factor hace que el polinomio sea igual a cero cuando sustituimos el factor para cada "x" en la ecuación.
- Vamos a empezar con nuestro primer factor, 1. Vamos a sustituir el "1" para cada "x" en la ecuación:
(1)3 - 4(1)2 - 7(1) + 10 = 0. - Esto nos da: 1 - 4 - 7 + 10 = 0.
- Debido a que 0 = 0 es una declaración verdadera, sabemos que x = 1 es una solución.
- Vamos a empezar con nuestro primer factor, 1. Vamos a sustituir el "1" para cada "x" en la ecuación:
-
4Reorganiza un poco. Si x = 1, podemos reorganizar el estado para verse un poco diferente sin cambiar su significado.
- "X = 1" es lo mismo que "x - 1 = 0" o "(x - 1)". Hemos restado un "1" de cada lado de la ecuación.
-
5Factoriza la raíz fuera del resto de la ecuación. "(X - 1)" es nuestra raíz. Vamos a ver si podemos factorizarlo del resto de la ecuación. Vamos a tomar un polinomio a la vez.
- ¿Podemos factorizar (x - 1) y x3? No, no se puede. Sabemos que puede pedir prestado un -x2 de la segunda variable, entonces lo podemos factorizar: x2(x - 1) = x3 - x2.
- ¿Podemos factorizar (x - 1) con lo que queda de nuestra segunda variable? No, otra vez no podemos. Tenemos que pedir prestado otro poco de la tercera variable. Tenemos que pedir prestado un 3x de -7x. Esto nos da -3x(x - 1) = -3x2 + 3x.
- Como tomamos un 3x de -7x, nuestra tercera variable es ahora -10x y nuestra constante es 10. ¿Podemos factorizar esto? ¡Podemos! -10(x - 1) = -10x + 10.
- Lo que hicimos fue reorganizar las variables para que pudiéramos factorizar (x - 1) de la ecuación completa. Nuestra ecuación reordenada se parece a esto: x3 - x2 - 3x2 + 3x - 10x + 10 = 0, pero sigue siendo lo mismo que x3 - 4x2 - 7x + 10 = 0.
-
6A continuación, sustituye por los factores de la expresión libre. Mira los números que factorizamos utilizando el (x - 1) en el paso 5:
- x2(x - 1) - 3x(x - 1) - 10(x - 1) = 0. Podemos arreglar esto para que sea mucho más fácil de factorizar una vez más: (x - 1)(x2 - 3x - 10) = 0.
- Solo estamos tratando de factorizar (x2 - 3x - 10) aquí. Esto se factoriza en (x + 2)(x - 5).
-
7Tus soluciones serán las raíces factorizadas. Puedes comprobar si las soluciones funcionan realmente conectando cada una, individualmente, en la ecuación original.
- (x - 1)(x + 2)(x - 5) = 0. Esto nos da soluciones de 1, -2 y 5.
- Conecta -2 en la ecuación: (-2)3 - 4(-2)2 - 7(-2) + 10 = -8 - 16 + 14 + 10 = 0.
- Conecta 5 en la ecuación: (5)3 - 4(5)2 - 7(5) + 10 = 125 - 100 - 35 + 10 = 0.
Consejos
- El polinomio cúbico es un producto de un polinomio de primer grado o el producto de un polinomio de primer grado y de otro polinomio de segundo grado sin factorizar. En este último caso utilizamos la división larga después de encontrar el polinomio de primer grado para obtener el polinomio de segundo grado.
- No hay polinomios cúbicos sin factorizar sobre los números reales porque cada cubo debe tener una raíz real. Los cubos como x^3 + x + 1 que tienen una raíz real irracional no se pueden factorizar en polinomios con coeficientes enteros o racionales. Mientras que puede ser factorizado con la fórmula cúbica, es irreducible como un polinomio entero.[5]
Referencias
- ↑ http://web.math.ucsb.edu/~vtkala/2016/S/4B/FactoringCubicPolynomials.pdf
- ↑ https://sciencing.com/solve-cubic-polynomials-2409.html
- ↑ https://www.mathsisfun.com/algebra/polynomials-solving.html
- ↑ https://www.dummies.com/education/math/pre-calculus/factoring-four-or-more-terms-by-grouping/
- ↑ https://kipkis.com/Factor_a_Cubic_Polynomial




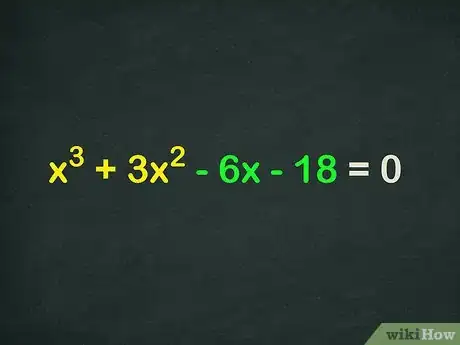
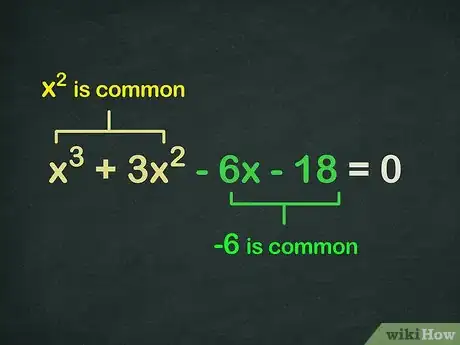
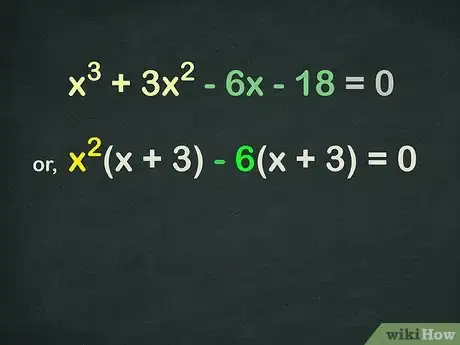
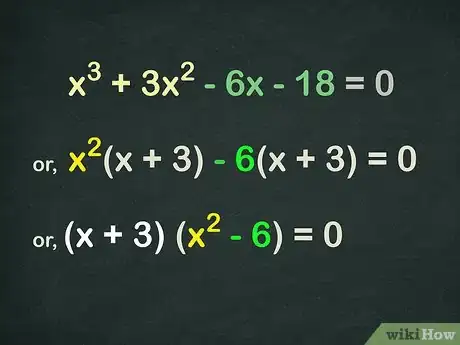

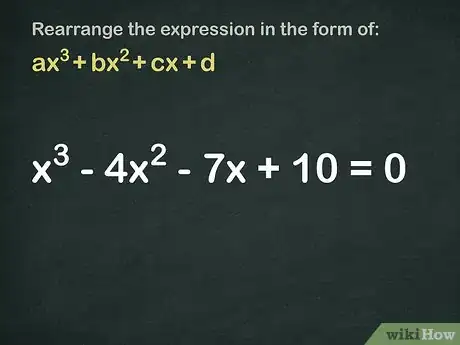
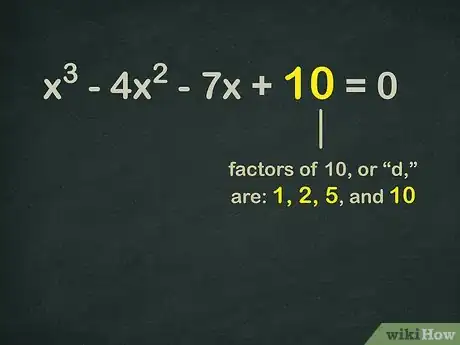
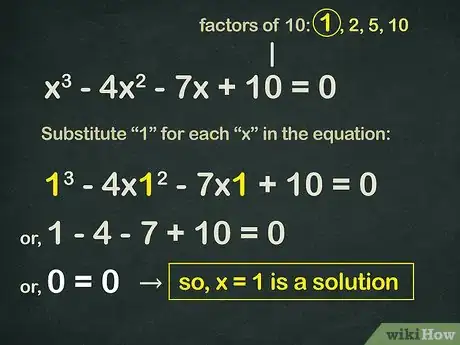
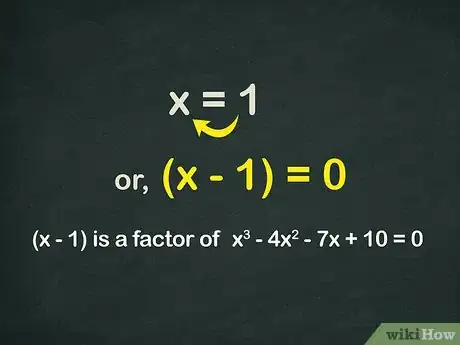
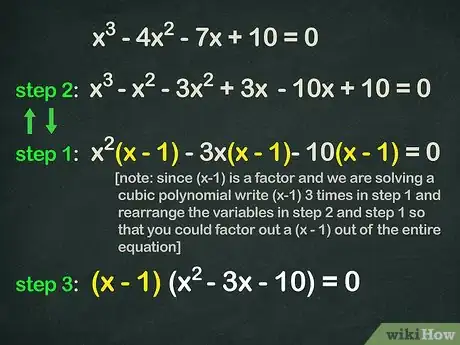
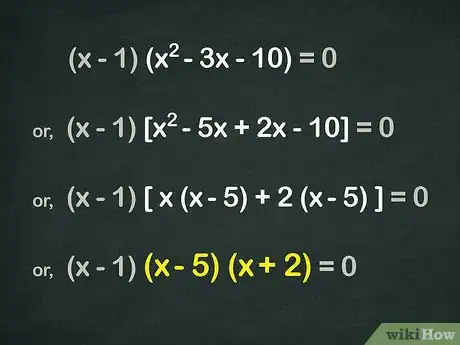

-Step-31-Version-2.webp)




-Step-31-Version-2.webp)