Nuestro equipo de editores e investigadores capacitados han sido autores de este artículo y lo han validado por su precisión y amplitud.
wikiHow's Content Management Team revisa cuidadosamente el trabajo de nuestro personal editorial para asegurar que cada artículo cumpla con nuestros altos estándares de calidad.
Este artículo ha sido visto 396 729 veces.
Gracias a las calculadoras, ahora solo hay que presionar un par de botones para hallar la raíz cúbica de cualquier número. Sin embargo, si no tienes calculadora o quieres impresionar a tus amigos con tu habilidad de calcular una raíz cúbica a mano, puedes usar los pasos de esta guía. Existe un proceso que al principio parece complicado, pero con algo de práctica te resultará cada vez más fácil. Si recuerdas las operaciones matemáticas básicas y los pasos de álgebra necesarios para elevar un número al cubo, ¡ya cuentas con algo de ventaja!
Pasos
Parte 1
Parte 1 de 3:Resolver un problema de ejemplo con raíz cúbica
-
1Plantea el problema. Resolver la raíz cúbica de un número es bastante parecido a resolver un problema de división larga, pero con algunas diferencias particulares. El primer paso es plantear el problema con el formato adecuado.[1]
- Anota el número para el cual vas a calcular la raíz cúbica. Anota los dígitos en grupos de tres, usando la coma decimal como punto de inicio. En este ejemplo, se calculará la raíz cúbica de 10. Escribe este número como 10, 000 000. Los ceros adicionales son para mejorar la precisión de la respuesta.
- Dibuja el símbolo de la raíz cúbica sobre el número. Este símbolo cumple la misma función que la línea de la barra de división. La única diferencia es la forma del símbolo.
- Coloca la coma decimal por encima de la línea del radical, justo arriba de la coma decimal del número original.
-
2Memoriza el cubo de los números de un dígito. Necesitarás usarlo para hacer algunos cálculos. A continuación, verás una lista de números de un dígito elevados al cubo:
-
3Encuentra el primer dígito de la solución. Elige un número tal que, elevado al cubo, te dé como resultado el mayor número posible, menor que el primer conjunto de tres números.[2]
- En este ejemplo, el primer conjunto de tres números es 10. Encuentra el mayor cubo perfecto menor a 10. Ese número es 8 y su raíz cúbica es 2.
- Anota el número 2 por encima de la línea del radical, justo arriba del número 10. Escribe el valor de , que es 8, debajo del número 10, traza una línea y resta ambos números, tal como lo harías en una división larga. El resultado es 2.
- Después de calcular la resta tendrás el primer dígito de la solución. Ahora deberás determinar si ese simple dígito es un resultado lo suficientemente preciso. En la mayoría de los casos, no lo será. Puedes comprobarlo elevando ese número al cubo y viendo si ese número es lo suficientemente cercano al resultado que necesitas. En este caso , es simplemente 8, lo cual no es un valor muy cercano a 10. Así que debes continuar.
-
4Prepárate para calcular el próximo dígito. Anota el próximo grupo de tres números junto al resto de la división y dibuja una pequeña línea vertical a la izquierda del número resultante. Ese número será la base sobre la cual trabajarás para encontrar el próximo dígito en la solución de la raíz cúbica. En este ejemplo, el número es 2000, que se forma con el resto 2 de la resta, unido al grupo de tres ceros que bajaste.[3]
- A la izquierda de la línea vertical, deberás obtener el próximo divisor como resultado de la suma de tres números separados. Crea los espacios para estos números dibujando tres guiones sobre los cuales escribirás más tarde los números, y separa estos espacios con signos más (+).
-
5Obtén los primeros dígitos del próximo divisor. Para obtener la primera parte del divisor, anota 300 por la raíz cuadrada de lo que esté arriba del símbolo del radical. En este caso, el número que está arriba del símbolo del radical es 2 y 22 es 4, y 4*300=1200. Por lo tanto, escribe 1200 en el primer espacio. El divisor que usarás en esta etapa de la solución será 1200, más otro número que obtendrás a continuación.[4]
-
6Encuentra el próximo número de la solución de esta raíz cúbica. Encuentra el próximo dígito de la solución seleccionando qué número puedes multiplicar por el divisor, 1200 algo, de forma tal que puedas restárselo al resto, que es 2000. Ese número solo puede ser 1, ya que 2 por 1200 sería 2400 y 2400 es mayor que 2000. Escribe el número 1 en el próximo espacio arriba del símbolo del radical.[5]
-
7Determina el resto del divisor. En este paso de la solución, el divisor se compone de tres partes. La primera parte son los 1200 que ya tienes. Para completar el divisor, ahora tienes que sumarle dos términos más a esos 1200.[6]
- Ahora calcula 3 por 10 por cada uno de los dos dígitos que están en la solución, arriba del símbolo del radical. En este problema de ejemplo, eso significa 3*10*2*1, lo cual es igual a 60. Súmalo a 1200 que ya tenías y obtendrás 1260.
- Finalmente, suma el cuadrado del último dígito. En este ejemplo, ese número es 1 y 12 sigue siendo 1. El divisor total es, por lo tanto, 1200+60+1 o 1261. Anota este número a la izquierda de la línea vertical.
-
8Multiplica y resta. Completa esta etapa de la solución multiplicando el último dígito de la solución (en este caso 1) por el divisor que acabas de calcular, 1261. 1*1261=1261. Anota este número debajo de 2000 y haz la resta. Obtendrás como resultado 739.
-
9Decide si es necesario continuar para obtener un número más preciso. Una vez que hayas completado la parte de la resta en cada paso, tendrás la posibilidad de evaluar si la respuesta es lo suficientemente precisa. Para la raíz cúbica de 10, después de la primera resta, la respuesta era 2, lo cual no era muy preciso. Ahora, después de la segunda resta, la solución se transformó en 2,1.[7]
- Puedes comprobar la precisión del resultado elevándolo al cubo: 2,1*2,1*2,1. El resultado es 9,261.
- Si crees que el resultado es lo suficientemente preciso, puedes terminar aquí. Si quieres una respuesta más precisa, entonces deberás continuar con otra ronda.
-
10Encuentra el divisor de la próxima ronda. En este caso, para seguir practicando y para obtener una respuesta más precisa, repite los pasos anteriores para completar una nueva ronda. Hazlo como se explica a continuación:[8]
- Baja el próximo grupo de tres dígitos. En este caso estos tres dígitos son tres ceros, que ahora acompañarán los 739 del resto y formarán 739 000.
- Comienza el divisor con 300 por el cuadrado del número que está actualmente arriba de la línea del radical. Este número es , lo que da como resultado 132 300.
- Selecciona el próximo dígito de la solución. Es un número que al multiplicarlo por 132 300 es menor a los 739 000 del resto. Una buena opción sería 5, ya que 5*132 300=661 500. Anota el dígito 5 en el próximo espacio arriba de la línea del radical.
- Multiplica 3 por el número que antes estaba sobre la línea del radical, 21, por el último dígito que acabas de anotar, 5, por 10. Esto es .
- Finalmente, eleva el último dígito al cuadrado. Esto es
- Suma todas las partes del divisor y obtendrás 132 300+3150+25=135 475.
-
11Multiplica el divisor por el número de la solución. Una vez que hayas calculado el divisor de esta otra ronda y hayas expandido la solución en un dígito más, continúa de la siguiente manera:
- Multiplica el divisor por el último dígito de la solución: 135 475*5=677 375.
- Resta: 739 000-677 375=61 625.
- Determina si la solución 2,15 es lo suficientemente precisa. Elévala al cubo para obtener .
-
12Anota la respuesta final. El resultado de arriba del radical es la raíz cúbica, ahora con una precisión de tres cifras significativas. En este ejemplo, la raíz cúbica de 10 es 2,15. Verifica que 2,153=9,94, lo cual es bastante cercano a 10. Si necesitas una respuesta aún más precisa, solo tienes que continuar con el proceso repitiendo los pasos tantas veces como lo desees.Anuncio
Parte 2
Parte 2 de 3:Encontrar raíces cúbicas por estimación repetida
-
1Utiliza números al cubo para establecer el límite superior y el límite inferior. Si te preguntan la raíz cúbica de cualquier número casi siempre puedes encontrar la respuesta comenzando con el cubo perfecto más cercano posible, pero sin exceder el número objetivo.
- Por ejemplo, si quieres hallar la raíz cúbica de 600, recuerda (o usa la tabla de números al cubo) que y . En consecuencia, la solución de la raíz cúbica de 600 debe estar entre el 8 y el 9. Para llegar a una solución, usa como límite inferior 512 y como límite superior 729.
-
2Estima el segundo dígito. El primer dígito lo obtuviste gracias a que conoces el valor de ciertos números elevados al cubo. Para el próximo dígito deberás estimar algún número entre 0 y 9 basándote en el lugar que ocupa el número objetivo entre los dos límites que definiste.
- Para este ejemplo, el objetivo 600 cae aproximadamente en el medio de los dos números de los límites 512 y 729. Así que sería una buena opción elegir el 5 como tu próximo dígito.
-
3Prueba tu estimación elevándola al cubo. Prueba con multiplicar la estimación con la que estás trabajando actualmente para ver qué tan cerca se encuentra del número objetivo.
- En este ejemplo, tienes que multiplicar .
-
4Ajusta la estimación según sea necesario. Una vez que hayas elevado tu estimación al cubo, comprueba dónde cae el resultado en comparación con tu número objetivo. Si el resultado supera al objetivo, tendrás que reducir la estimación en uno o más. Si el resultado está por debajo del objetivo, tendrás que ajustar hacia arriba hasta superar el objetivo.
- Por ejemplo, en este problema, es mayor al número objetivo, que es 600. Por lo tanto deberás reducir la estimación a 8,4. Eleva al cubo este número y compáralo con tu objetivo. Verás que . Este número ahora es inferior al objetivo. Por lo tanto, sabes que la raíz cúbica de 600 debe ser como mínimo 8,4 pero inferior a 8,5.
-
5Estima el próximo dígito para mayor precisión. Puedes continuar con este proceso de estimación de dígitos entre 0 y 9 hasta que tu respuesta sea tan precisa como quieras. En cada ronda de estimación, comienza por observar qué tan cerca o lejos de los dos límites cayó la última estimación que hiciste.
- En este ejemplo, durante la última ronda de cálculo comprobaste que , mientras que . El objetivo de 600 se encuentra un poco más cerca de 592 que de 614. Por lo tanto, en la próxima estimación comienza con un número que se encuentre antes de la mitad entre 0 y 9. Un buen candidato sería el 4, por lo que la raíz cúbica estimada ahora es 8,44.
-
6Continúa evaluando las estimaciones y haciendo ajustes. Eleva al cubo tus estimaciones tantas veces como sea necesario para comprobar qué tan cerca estás del objetivo. Debes encontrar los números que están justo debajo y justo arriba del número objetivo.
- Siguiendo con el ejemplo, ahora calcula . Este valor se encuentra apenas por encima del objetivo, así que baja un lugar y prueba con 8,43. Esto te dará . Por lo tanto, sabes que la raíz cúbica de 600 es algún número superior a 8,43 pero inferior a 8,44.
-
7Continúa repitiendo estas operaciones tantas veces como lo desees para mejorar la precisión. Repite estos pasos de estimación, comparación y reestimación todas las veces que sea necesario hasta que la solución sea lo suficientemente precisa. Ten en cuenta que por cada lugar decimal que agregas, el número objetivo se acerca más y más al número original.
- Para el ejemplo de la raíz cúbica de 600, cuando tenías dos lugares decimales (8,43), estabas a menos de 1 unidad de distancia del objetivo. Si continúas y agregas un tercer lugar decimal, descubrirás que , lo cual está a menos de 0,1 de distancia de la respuesta correcta.
Anuncio
Parte 3
Parte 3 de 3:Entender cómo funcionan estos cálculos
-
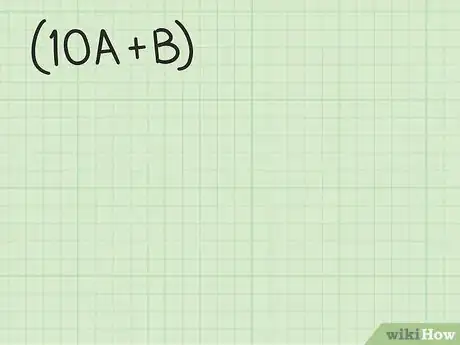
1Repasa la expansión de binomios. Para comprender cómo es que funciona este algoritmo para encontrar raíces cúbicas, primero recuerda que la expansión de un término al cubo se ve similar a la de un binomio. Probablemente aprendiste esto Álgebra o Álgebra II en la escuela secundaria (y, si eres como la mayoría de las personas, probablemente lo olvidaste al poco tiempo). Selecciona dos variables y para representar números de un solo dígito. Luego crea el binomio para representar un número de dos dígitos.[9]
- El hecho de usar el término es lo que crea un número de dos dígitos. Independientemente del dígito que selecciones para , el dígito siempre se pondrá en la columna de las decenas. Por ejemplo, si es 2 and es 6, entonces sería 26.[10]
-
2Expande el binomio elevándolo al cubo. Ahora deberás trabajar hacia atrás, creando primero el cubo para luego ver por qué funciona la raíz cúbica. Tienes que averiguar el valor de . Puedes hacerlo multiplicando . Estos pasos son demasiado largos como para mostrarlos aquí, pero el resultado final es .[11]
- Para mayor información sobre cómo expandir el binomio y llegar a este resultado, puedes leer el artículo Cómo multiplicar binomios. Si quieres usar una versión más avanzada pero más corta, utiliza el método del triángulo de Pascal para calcular (x+y)n.
-
3Reconoce el significado del algoritmo de división larga. Como habrás observado, el método para calcular la raíz cúbica funciona en forma similar al de una división larga. En la división larga, encuentras dos factores que se multiplican para dar el producto del número con el cual empezaste. En estos cálculos, el número que quieres hallar (el número que termina quedando arriba del signo del radical) es la raíz cúbica. Esto significa que ese número representa el término (10A+B). Por ahora, A y B son irrelevantes, siempre y cuando entiendas la relación que existe entre esos números y la respuesta.[12]
-
4Revisa la versión expandida. Cuando mires al polinomio expandido, podrás observar por qué funciona el algoritmo de la raíz cúbica. Observa que el divisor de cada paso del algoritmo es la suma de los cuatro términos que necesitas calcular y sumar. Estos términos se obtienen debido a lo siguiente:[13]
- El primer término contiene un múltiplo de 1000. Es el primer número que puedes elevar al cubo y permanecer dentro del rango de la división larga para el primer dígito. Así obtienes el término 1000A^3 en la expansión del binomio.
- El segundo término de la expansión del binomio tiene un coeficiente de 300 (esto, de hecho, proviene de ). Recuerda que, en el cálculo de la raíz cúbica, el primer dígito se multiplicaba por 300 en cada paso.
- El segundo dígito, en cada paso del cálculo de la raíz cúbica, proviene del tercer término de la expansión del binomio. En la expansión del binomio puedes ver que aparece el término 30AB^2.
- El dígito final de cada paso es el término B^3.
-
5Observa cómo aumenta la precisión. A medida que vas siguiendo el algoritmo de la división larga, cada paso que terminas le proporciona más precisión a la respuesta. Por ejemplo, en este artículo se trabajó con un caso de ejemplo que consistía en calcular la raíz cúbica de 10. En el primer paso, la solución era simplemente 2 porque está cerca de la respuesta, pero es menor a 10. De hecho, . Después de la segunda ronda, la solución a la que llegaste es 2,1. Cuando verificaste el resultado, viste que , lo cual estaba mucho más cerca del valor deseado, que en este caso era 10. Después de una tercera ronda, llegaste al número 2,15, que elevado al cubo era . Así puedes seguir trabajando con grupos de tres dígitos hasta obtener una respuesta tan precisa como lo desees.[14]Anuncio
Consejos
- Tal como sucede siempre en matemática, la práctica hace al maestro. Mientras más practiques, más experto te volverás en este cálculo.
Advertencias
- Es fácil cometer algún error en los cálculos. Revisa cuidadosamente tu trabajo y verifícalo.
Cosas que necesitarás
- bolígrafo o lápiz
- hoja de papel
- regla
- goma de borrar
Referencias
- ↑ https://xlinux.nist.gov/dads/HTML/cubeRoot.html
- ↑ https://xlinux.nist.gov/dads/HTML/cubeRoot.html
- ↑ https://xlinux.nist.gov/dads/HTML/cubeRoot.html
- ↑ https://xlinux.nist.gov/dads/HTML/cubeRoot.html
- ↑ https://xlinux.nist.gov/dads/HTML/cubeRoot.html
- ↑ https://xlinux.nist.gov/dads/HTML/cubeRoot.html
- ↑ https://xlinux.nist.gov/dads/HTML/cubeRoot.html
- ↑ https://xlinux.nist.gov/dads/HTML/cubeRoot.html
- ↑ https://xlinux.nist.gov/dads/HTML/cubeRoot.html




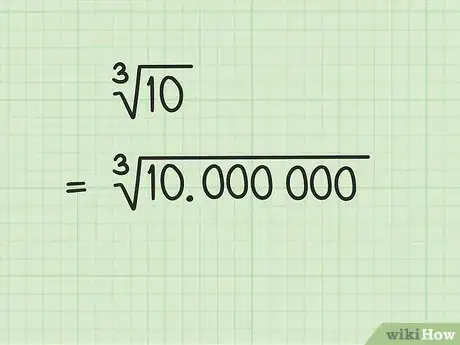
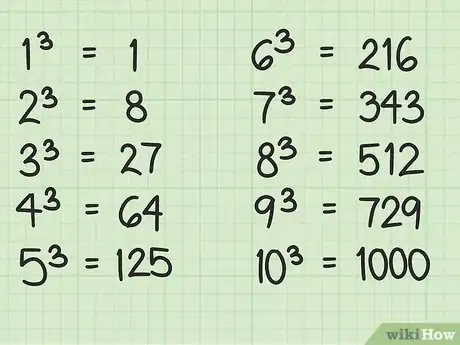










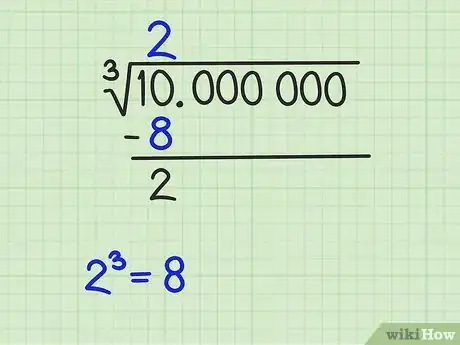

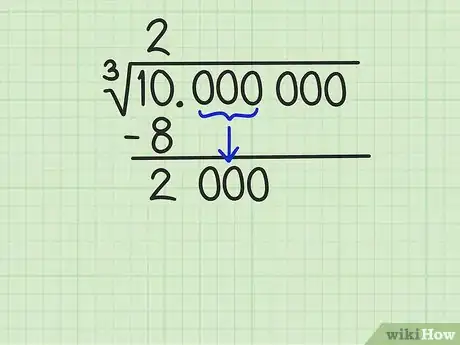
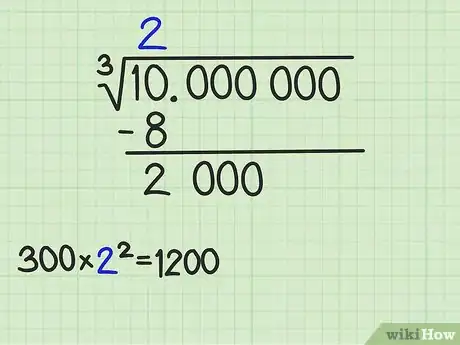

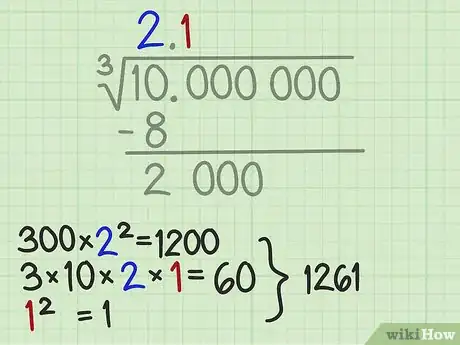
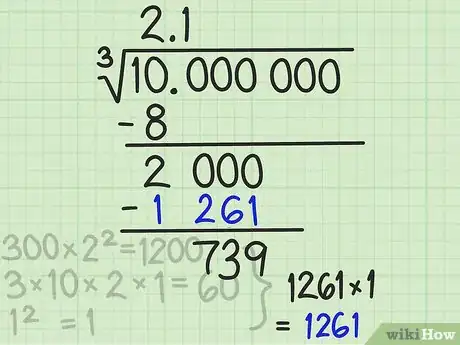
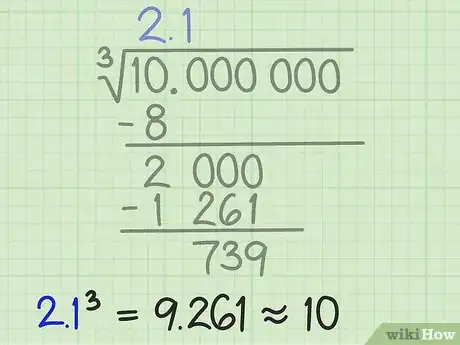







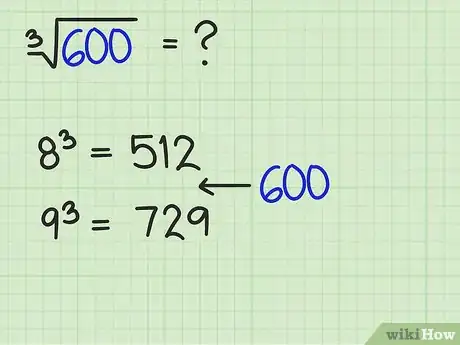


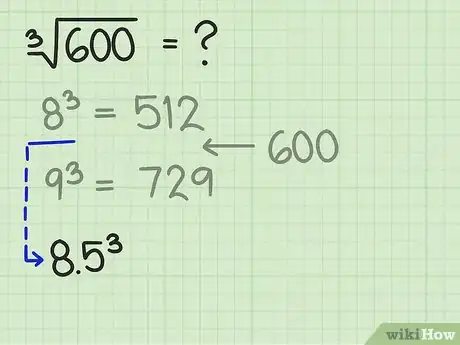
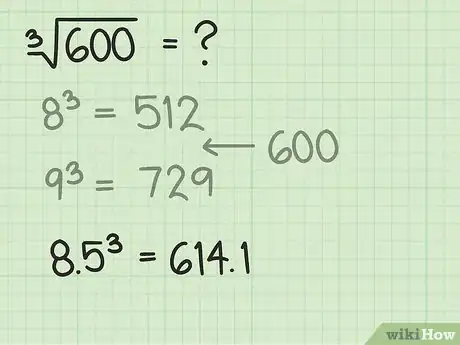

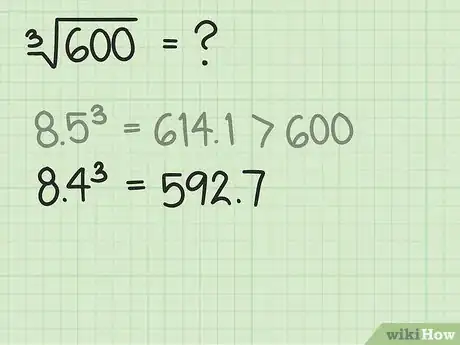


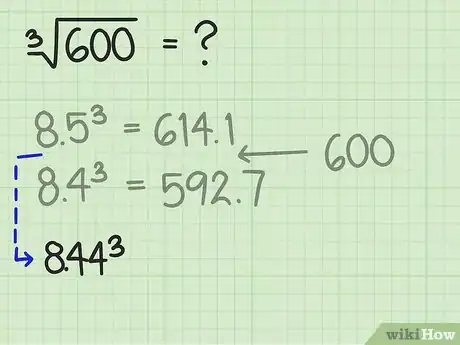


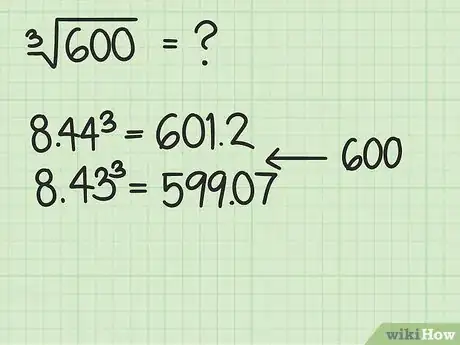













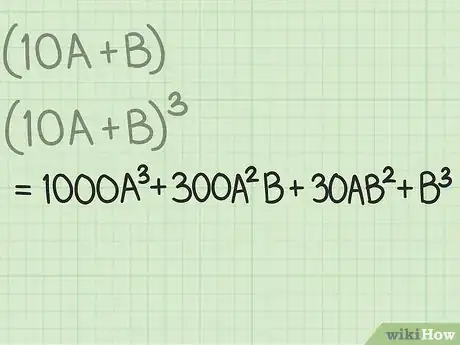

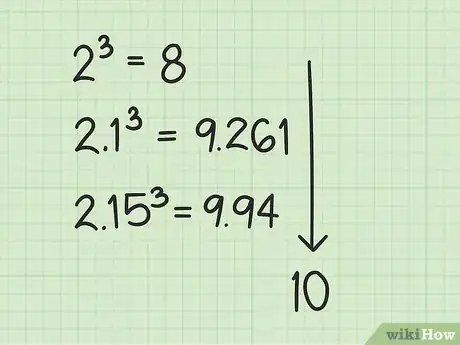






















wikiHow's Content Management Team revisa cuidadosamente el trabajo de nuestro personal editorial para asegurar que cada artículo cumpla con nuestros altos estándares de calidad. Este artículo ha sido visto 396 729 veces.