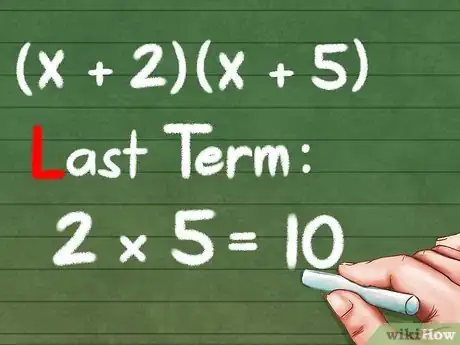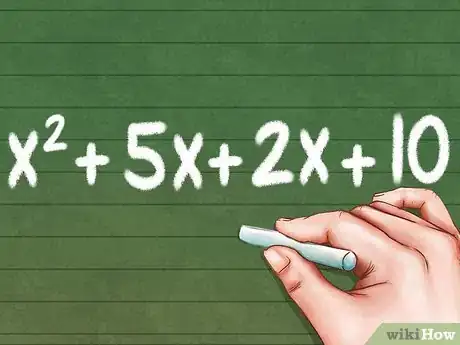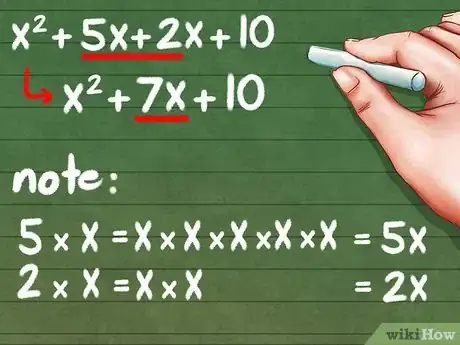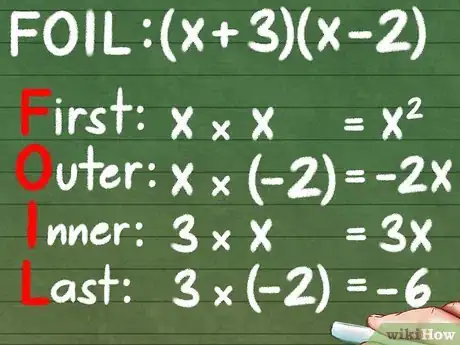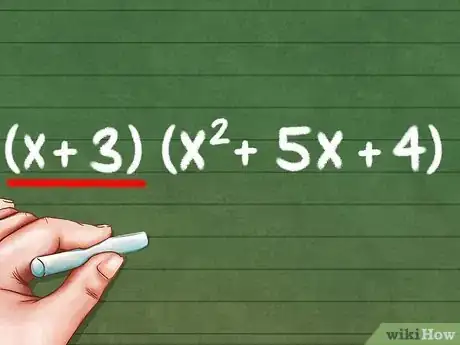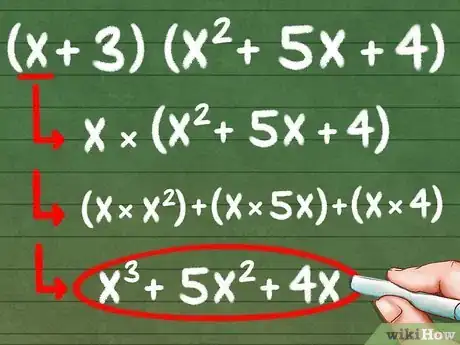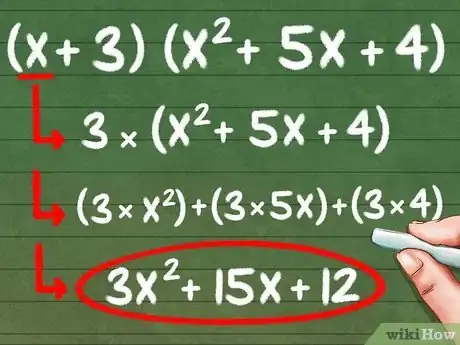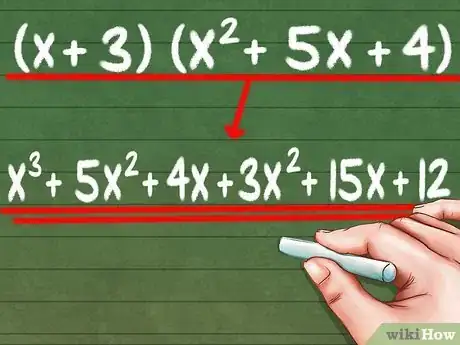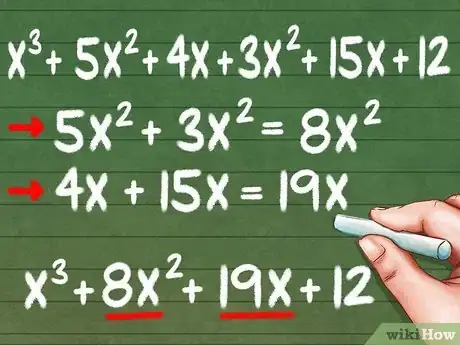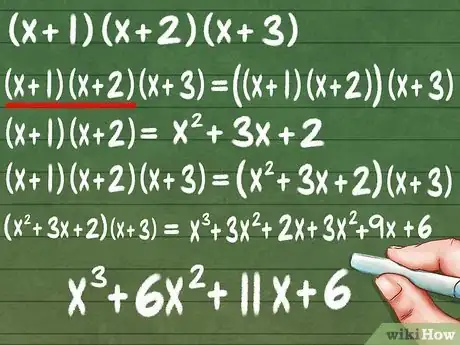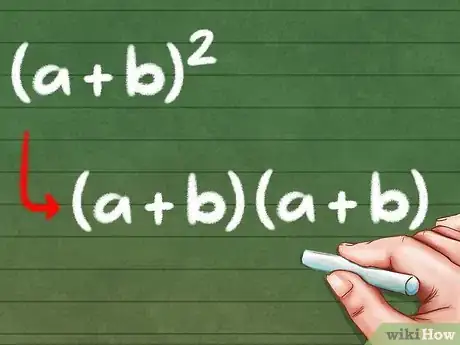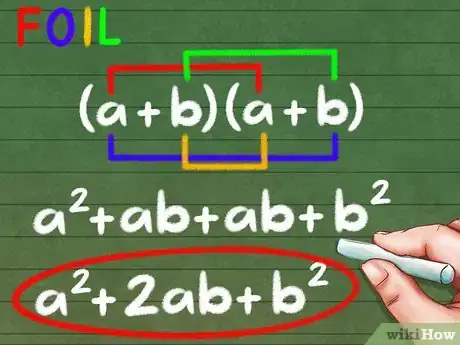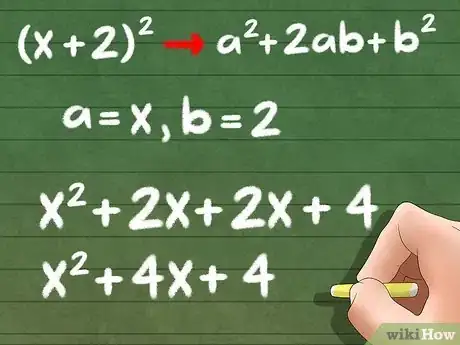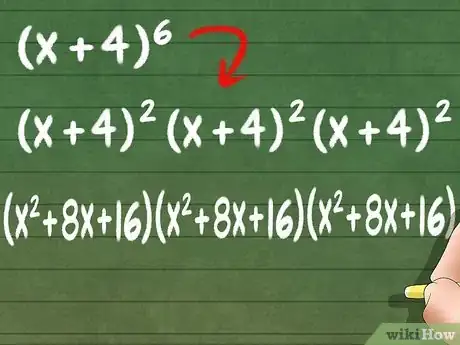Cómo multiplicar binomios

Los binomios constituyen expresiones matemáticas pequeñas que consisten de un término variable (x, a, 3x, 4t, 1090y) al que se le suma o resta un término constante (1, 3, 110, etc.). Los binomios siempre tienen solo dos términos, aunque constituyen los cimientos de ecuaciones mucho más grandes y complejas a las que se les conoce como polinomios, por lo que es extremadamente importante aprenderlos bien. En este artículo, se abordarán varios tipos de multiplicaciones de binomios, aunque también puedes aprenderlos todos por separado.

Método 1
Método 1 de 3:
Multiplicar dos binomios

  1. Imagen titulada Multiply Binomials Step 1
    1
    Comprende el vocabulario matemático y los tipos de preguntas. Resolver las preguntas en tu próximo examen sería imposible si no supieras lo que se te pregunta. Por fortuna, la terminología no es de gran dificultad:
    • Términos: un término simplemente constituye una parte de la ecuación que se suma o se resta. Puede ser una constante, una variable o ambas. Por ejemplo, los términos de 12 + 13x + 4x2, son 12, 13x y 4x2.[1]
    • Binomio: esta es apenas una forma complicada de referirse a "una expresión que contiene dos términos", como x + 3 o x4 - 3x.[2]
    • Potencias: se refiere al exponente de un término.[3] Por ejemplo, se podría decir que x2 es "x a la segunda potencia."
    • Una pregunta que te pida "encontrar los términos de dos binomios (x + 3)(x + 2)", "encontrar el producto de dos binomios" o "expandir los dos binomios", te pide que los multipliques.
  2. Imagen titulada Multiply Binomials Step 2
    2
    Aprende el acrónimo FOIL para recordar el orden de multiplicación de los binomios. FOIL es una guía simple para la multiplicación de dos binomios que representa el orden en el que se deben multiplicar sus partes: F es la sigla en inglés de primeros, O es la sigla en inglés de exteriores, I es la sigla en inglés de interiores y L es la sigla en inglés de últimos. Estas palabras se refieren al orden en el que están escritos los términos. Imagina que vamos a multiplicar los binomios (x + 2) y (x + 5). Estos serían los términos:[4]
    • Primeros: x y x
    • Exteriores: x y 5
    • Interiores: 2 y x
    • Últimos: 2 y 5
  3. Imagen titulada Multiply Binomials Step 3
    3
    Multiplica la PRIMERA parte de cada paréntesis.[5] Esto constituye la F de FOIL. Siguiendo con el ejemplo (x + 2)( x + 5), los primeros términos son "x" y "x". Debes multiplicarlos y tomar nota de la respuesta: "x2".
    • Primer término: x * x = x2
  4. Imagen titulada Multiply Binomials Step 4
    4
    Multiplica las partes EXTERIORES de cada paréntesis. [6] Esto constituye los dos "extremos" exteriores del problema. Entonces, siguiendo con el ejemplo (x + 2)(x + 5), estos serían "x" y "5". Al multiplicarlos, obtienes "5x".
    • Término exterior: x * 5 = 5x
  5. Imagen titulada Multiply Binomials Step 5
    5
    Multiplica las partes INTERIORES de cada paréntesis. [7] Los términos interiores serán los dos números que estén más cerca del centro. En el caso de (x + 2)(x + 5), esto quiere decir que debes multiplicar "2" y "x" para obtener "2x".
    • Término interior: 2 * x = 2x
  6. Imagen titulada Multiply Binomials Step 6
    6
    Multiplica las ÚLTIMAS partes de cada paréntesis. [8] Esto no se refiere a los dos últimos números, sino al último número de cada paréntesis. Entonces, para el ejemplo (x + 2)(x + 5), debemos multiplicar el "2" y el "5" y obtendríamos "10".
    • El último término: 2 * 5 = 10
  7. Imagen titulada Multiply Binomials Step 7
    7
    Suma todos los términos nuevos. Suma los términos para combinarlos de forma que se cree una expresión nueva y más grande.[9] Siguiendo con el ejemplo anterior, obtendríamos la ecuación:
    • x2 + 5x + 2x + 10
  8. Imagen titulada Multiply Binomials Step 8
    8
    Simplifica los términos similares. Los términos similares constituyen las partes de la ecuación que tengan la misma variable y potencia. En el caso del ejemplo, los términos 2x y 5x tienen ambos una x y se pueden sumar. Debido a que ninguno de los demás términos es similar, se quedan tal y como están.
    • Respuesta final: (x + 2)(x + 5) = x2 + 7x + 10
    • Nota avanzada: si quieres aprender la forma como funcionan los términos similares, recuerda los conceptos básicos de la multiplicación. Por ejemplo, 3 * 5 quiere decir que debes sumar tres números 5 para obtener 15 (5 + 5 + 5). La ecuación contiene 5 * x (x + x + x + x + x) y 2 * x (x + x). Al sumar todas las x en la ecuación, obtenemos siete variables x o 7x.
  9. Imagen titulada Multiply Binomials Step 9
    9
    No olvides que los números que se restan son negativos. Si se resta un número, esto constituye lo mismo que sumar un número negativo. Si olvidas conservar el signo de menos en el transcurso del cálculo, obtendrás la respuesta incorrecta. Observa el ejemplo (x + 3)(x - 2):
    • Primeros: x * x = x2
    • Exteriores: x * -2 = -2x
    • Interiores: 3 * x = 3x
    • Últimos: 3 * -2 = -6
    • Suma todos los términos: x2 - 2x + 3x - 6
    • Simplifica para obtener la respuesta final: x2 + x - 6
    Anuncio

Método 2
Método 2 de 3:
Multiplicar más de dos binomios

  1. Imagen titulada Multiply Binomials Step 10
    1
    Multiplica los dos primeros binomios ignorando el tercero por el momento. [10] Considera el ejemplo (x + 4)(x + 1)(x + 3). Es necesario multiplicar los binomios uno por uno. Por tanto, debes multiplicar dos términos cualesquiera siguiendo ya sea el método FOIL o la distribución de los términos. Si multiplicas los dos primeros (x + 4) y (x + 1) siguiendo el método FOIL, esto se vería así:
    • Primeros: x * x = x2
    • Exteriores: 1 * x = x
    • Interiores: 4 * x = 4x
    • Últimos: 1 * 4 = 4
    • Suma los términos: x2 + x + 4x + 4
    • (x + 4)(x + 1) = x2 + 5x + 4
  2. Imagen titulada Multiply Binomials Step 11
    2
    Suma el binomio restante a tu nueva ecuación. [11] Una vez que hayas multiplicado una parte de la ecuación, puedes lidiar con el binomio restante. Siguiendo con el ejemplo (x + 4)(x + 1)(x + 3), el término restante es (x + 3). Vuelve a colocarlo junto con la ecuación nueva para obtener: (x + 3)(x2 + 5x + 4).
  3. Imagen titulada Multiply Binomials Step 12
    3
    Multiplica el primer número del binomio por los tres números del otro paréntesis. Esto se conoce como la distribución de términos. Entonces, para la ecuación (x + 3)(x2 + 5x + 4), es necesario multiplicar la primera x por las tres partes del segundo paréntesis, "x2", "5x" y "4".
    • (x * x2) + (x * 5x) + (x * 4) = x3 + 5x2 + 4x
    • Toma nota de esta respuesta y guárdala para más adelante.
  4. Imagen titulada Multiply Binomials Step 13
    4
    Multiplica el segundo número del binomio por los tres números del otro paréntesis. Considera la ecuación (x + 3)(x2 + 5x + 4). Ahora, multiplica la segunda parte del binomio por las tres partes del otro paréntesis, "x2", "5x" y "4".
    • (3 * x2) + (3 * 5x) + (3 * 4) = 3x2 + 15x + 12
    • Toma nota de esta respuesta junto a la primera.
  5. Imagen titulada Multiply Binomials Step 14
    5
    Suma las dos respuestas de la multiplicación. Es necesario sumar las respuestas de los dos pasos anteriores, ya que conforman las dos partes de la respuesta final.
    • x3 + 5x2 + 4x + 3x2 + 15x + 12
  6. Imagen titulada Multiply Binomials Step 15
    6
    Simplifica la ecuación y obtendrás la respuesta final. Todos los términos "similares" (es decir, los términos que tengan la misma variable y potencia, como 5x2 y 3x2), pueden sumarse para que la respuesta sea más simple.[12]
    • 5x2 y 3x2 se convierten en 8x2.
    • 4x y 15x se convierten en 19x.
    • (x + 4)(x + 1)(x + 3) = x3 + 8x2 + 19x + 12
  7. Imagen titulada Multiply Binomials Step 16
    7
    Emplea siempre la distribución para abordar los problemas más grandes de multiplicación. Es posible emplear la distribución de términos para multiplicar ecuaciones de cualquier longitud, por lo que ahora cuentas con las herramientas necesarias para resolver problemas más grandes, como (x + 1)(x + 2)(x + 3). Multiplica dos binomios cualesquiera, ya sea mediante la distribución de términos o mediante FOIL, y luego multiplica el último binomio por los dos primeros mediante la distribución de términos. En el siguiente ejemplo, utilizamos FOIL para multiplicar (x + 1)(x + 2) y luego distribuimos los términos con (x + 3) para obtener la respuesta final:
    • (x + 1)(x + 2)(x + 3) = (x + 1)(x + 2) * (x + 3)
    • (x + 1)(x + 2) = x2 + 3x + 2
    • (x + 1)(x + 2)(x + 3) = (x2 + 3x + 2) * (x + 3)
    • (x2 + 3x + 2) * (x + 3) = x3 + 3x2 + 2x + 3x2 + 9x + 6
    • Simplifica para obtener la respuesta final: x3 + 6x2 + 11x + 6
    Anuncio

Método 3
Método 3 de 3:
Elevar binomios al cuadrado

  1. Imagen titulada Multiply Binomials Step 17
    1
    Conoce la forma de disponer "fórmulas generales". Mediante las fórmulas generales, puedes simplemente reemplazar los números en lugar de calcular FOIL cada vez. Los binomios elevados a la segunda potencia, como (x + 2)2, o a la tercera, como (4y + 12)3, pueden encajar con facilidad dentro de una fórmula preexistente para que resolverlos sea rápido y fácil. Puedes encontrar la fórmula general reemplazando todos los números por variables y luego, al final, puedes volver a reemplazar los números para obtener la respuesta. Empieza por la ecuación (a + b)2, en donde:
    • a representa el término variable (es decir, 4y - 1, 2x2 + 3, etc.). En caso de que no haya un número, a = 1 debido a que 1 * x = x.
    • b representa la constante que se suma o se resta (es decir, x + 10, t - 12).
  2. Imagen titulada Multiply Binomials Step 18
    2
    Ten en cuenta que los binomios elevados al cuadrado pueden reescribirse. [13] Si bien (a + b)2 podría parecer más complicado que el ejemplo anterior, no olvides que elevar un número al cuadrado constituye apenas multiplicarlo por sí mismo, por lo que es posible reescribir la ecuación de forma que tenga un aspecto más familiar:
    • (a + b)2 = (a + b)(a + b)
  3. Imagen titulada Multiply Binomials Step 19
    3
    Resuelve la ecuación nueva empleando FOIL. [14] Al utilizar FOIL en esta ecuación, obtenemos una fórmula general que se asemeja a la solución a cualquier multiplicación de binomios. No olvides que el orden no importa en la multiplicación:
    • Reescríbelo como (a + b)(a + b).
    • Primeros: a * a = a2
    • Interiores: b * a = ba
    • Exteriores: a * b = ab
    • Últimos: b * b = b2.
    • Suma los términos nuevos: a2 + ba + ab + b2
    • Combina los términos similares: a2 + 2ab + b2
    • Nota avanzada: los exponentes y radicales se consideran operaciones hiper-3, mientras que la multiplicación y la división constituyen operaciones hiper-2, lo que significa que las propiedades de la multiplicación y la división no funcionan para los exponentes. (a + b)2 no es lo mismo que a2 + b2. Este es un error muy común que la gente comete.
  4. Imagen titulada Multiply Binomials Step 20
    4
    Resuelve los problemas empleando la ecuación general a2 + 2ab + b2. Considera la ecuación (x + 2)2. No lleves a cabo FOIL de nuevo; en cambio, puedes reemplazar el primer término por "a" y el segundo por "b".
    • Ecuación general: a2 + 2ab + b2
    • a = x, b = 2
    • x2 + (2 * x * 2) + 22
    • Respuesta final: x2 + 4x + 4.
    • Siempre es posible revisar tu trabajo llevando a cabo FOIL en la ecuación original, (x + 2)(x + 2). Si lo haces correctamente, obtendrás la misma respuesta cada vez.
    • En caso de que se reste un término, de todas formas debe permanecer negativo en la ecuación general.
  5. Imagen titulada Multiply Binomials Step 21
    5
    No olvides introducir todo el término en la ecuación general. Dado el binomio (2x + 3)2, no debes olvidar que a = 2x, no simplemente a = 2. Al lidiar con términos complejos, es necesario recordar que tanto el 2 como la x se elevan al cuadrado.
    • Ecuación general: a2 + 2ab + b2
    • Reemplaza a y b: (2x)2 + 2(2x)(3) + 32
    • Eleva todos los términos al cuadrado: (22)(x2) + 14x + 32
    • Simplifica para obtener la respuesta final: 4x2 + 14x + 9
    Anuncio

Consejos

  • Conforme los binomios vayan tornándose más grandes, quizás sea necesario aprender un teorema más complejo conocido como la expansión de binomios.[15]
Anuncio

wikiHows relacionados

calcular el diámetro de un círculo
Cómo
calcular el diámetro de un círculo
calcular un incremento en porcentaje
Cómo
calcular un incremento en porcentaje
calcular la variación porcentual
Cómo
calcular la variación porcentual
encontrar el valor de X
Cómo
encontrar el valor de X
medir milímetros
Cómo
medir milímetros
calcular una frecuencia
Cómo
calcular una frecuencia
calcular las probabilidades de sacarte la lotería
Cómo
calcular las probabilidades de sacarte la lotería
convertir de grados a radianes
Cómo
convertir de grados a radianes
calcular la varianza
Cómo
calcular la varianza
calcular la incertidumbre
Cómo
calcular la incertidumbre
convertir radianes a grados
Cómo
convertir radianes a grados
calcular la velocidad
Cómo
calcular la velocidad
calcular el porcentaje de error
Cómo
calcular el porcentaje de error
encontrar una raíz cuadrada sin una calculadora
Cómo
encontrar una raíz cuadrada sin una calculadora
Anuncio

Referencias

  1. ↑ https://www.mathsisfun.com/definitions/term.html
  2. ↑ https://www.mathsisfun.com/definitions/binomial.html
  3. ↑ https://www.mathsisfun.com/definitions/power.html
  4. ↑ https://www.mathsisfun.com/definitions/foil-method.html
  5. ↑ http://www.mesacc.edu/~scotz47781/mat120/notes/polynomials/foil_method/foil_method.html
  6. ↑ http://www.mesacc.edu/~scotz47781/mat120/notes/polynomials/foil_method/foil_method.html
  7. ↑ http://www.mesacc.edu/~scotz47781/mat120/notes/polynomials/foil_method/foil_method.html
  8. ↑ http://www.mesacc.edu/~scotz47781/mat120/notes/polynomials/foil_method/foil_method.html
  9. ↑ https://courses.lumenlearning.com/prealgebra/chapter/multiplying-two-binomails-using-the-foil-method/
  1. ↑ https://www.youtube.com/watch?v=WNwfqkFhMbI
  2. ↑ https://youtube/WNwfqkFhMbI?t=30
  3. ↑ http://www.dunwoody.edu/pdfs/Elftmann-Simplify%20Binomials.pdf
  4. ↑ https://www.khanacademy.org/math/algebra/introduction-to-polynomial-expressions/special-products-of-polynomials/v/square-a-binomial
  5. ↑ http://www.algebra-class.com/binomial.html
  6. ↑ https://www.mathsisfun.com/algebra/binomial-theorem.html

Acerca de este wikiHow

wikiHow es un "wiki", lo que significa que muchos de nuestros artículos están escritos por varios autores. Para crear este artículo, 12 personas, algunas anónimas, han trabajado para editarlo y mejorarlo con el tiempo. Este artículo ha sido visto 9956 veces.
Categorías: Matemáticas
Anuncio