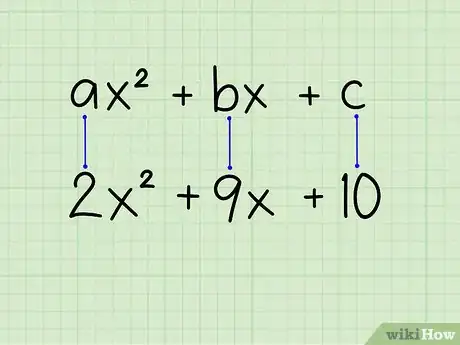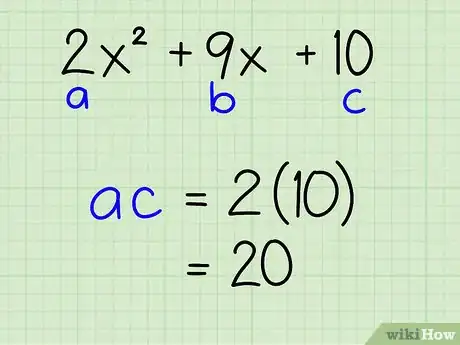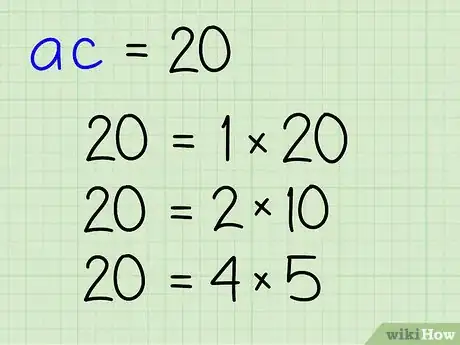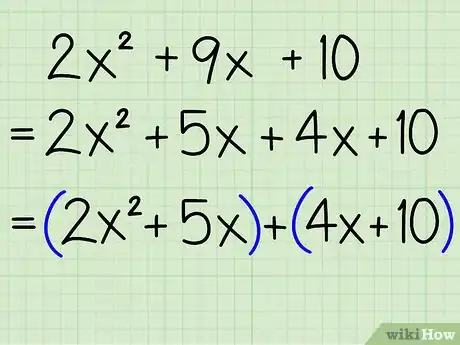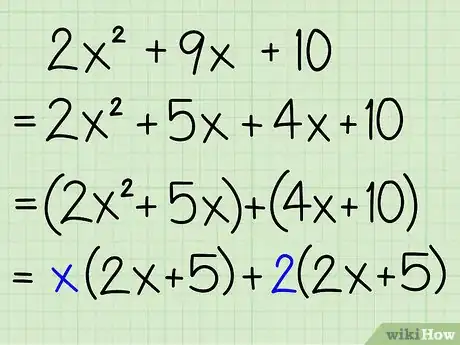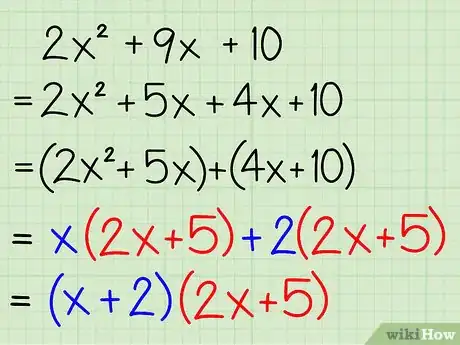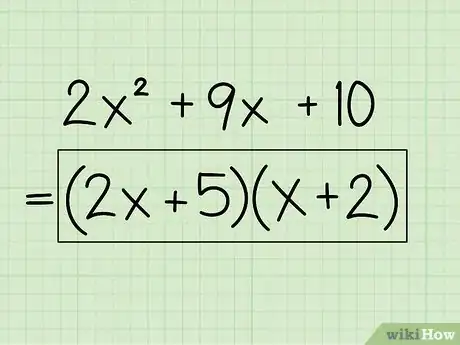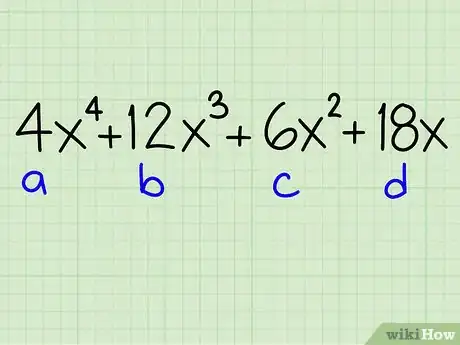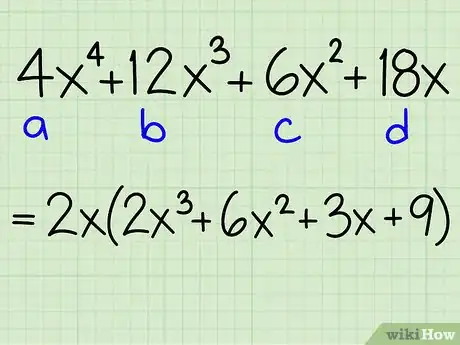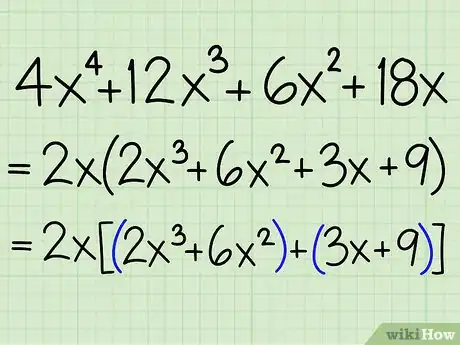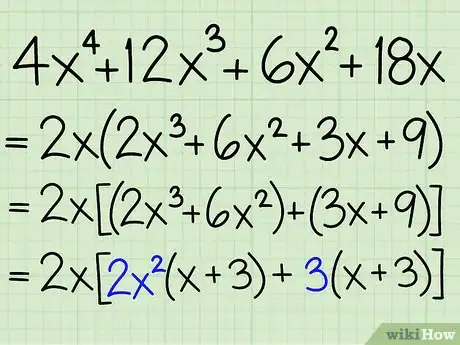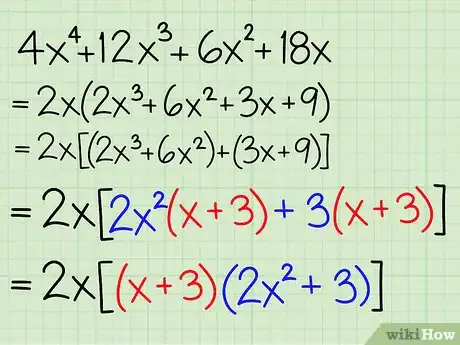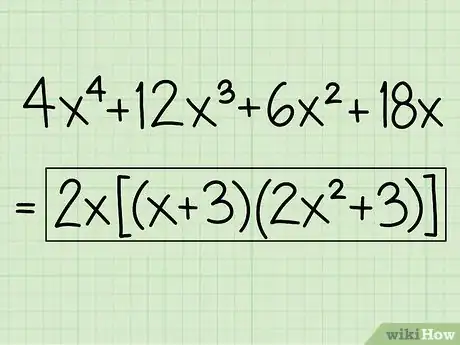Cómo factorizar por agrupación

La agrupación es una técnica específica que se usa para factorizar las ecuaciones polinómicas. Puedes usarla con ecuaciones cuadráticas y polinomios que tengan cuatro términos. Los dos métodos son similares, pero varían ligeramente.

Método 1
Método 1 de 2:
Ecuaciones cuadráticas[1]

  1. Imagen titulada Factor by Grouping Step 1
    1
    Observa la ecuación. Si planeas usar este método, la ecuación debe obedecer un formato básico: ax2 + bx + c
    • Por lo general, se usa este proceso cuando el coeficiente principal (el término a) es un número distinto a 1, pero también se puede usar para ecuaciones cuadráticas donde a = 1.
    • Por ejemplo: 2x2 + 9x + 10
  2. Imagen titulada Factor by Grouping Step 2
    2
    Halla el producto maestro. Multiplica el término a y el término c. El producto de estos dos términos se conoce como el producto maestro.
    • Por ejemplo: 2x2 + 9x + 10
      • a = 2; c = 10
      • a * c = 2 * 10 = 20
  3. Imagen titulada Factor by Grouping Step 3
    3
    Separa el producto maestro en su par de factores. Enumera los factores de tu producto maestro, sepáralos en sus pares naturales (los pares que se necesitan para obtener el producto maestro).
    • Por ejemplo: los factores de 20 son: 1, 2, 4, 5, 10, 20
      • Si se escriben en pares de factores: (1, 20), (2, 10), (4, 5)
  4. Imagen titulada Factor by Grouping Step 4
    4
    Halla el par de factores cuya suma sea igual a b. Revisa los pares de factores y determina con qué conjunto se obtendrá el término b (el término del medio y el coeficiente x) cuando se suman.
    • Si tu producto maestro fue negativo, necesitarás hallar un par de factores que sean igual al término b cuando se sustrae uno del otro.
    • Por ejemplo: 2x2 + 9x + 10
      • b = 9
      • 1 + 20 = 21; este no es el par correcto
      • 2 + 10 = 12; este no es el par correcto
      • 4 + 5 = 9; este sí es el par correcto
  5. Imagen titulada Factor by Grouping Step 5
    5
    Divide el término del centro en los dos factores. Modifica el término del centro, dividiéndolo en el par de factores que se identificó previamente. Asegúrate de incluir los signos adecuados (positivo o negativo).
    • Observa que el orden de los términos del centro no debe importar en este problema. Sin importar en qué orden escribas los términos, el resultado final será el mismo.
    • Por ejemplo: 2x2 + 9x + 10 = 2x2 + 5x + 4x + 10
  6. Imagen titulada Factor by Grouping Step 6
    6
    Agrupa los términos para que formen pares. Agrupa los primeros dos términos en un par y los segundos dos términos en otro par.
    • Por ejemplo: 2x2 + 5x + 4x + 10 = (2x2 + 5x) + (4x + 10)
  7. Imagen titulada Factor by Grouping Step 7
    7
    Excluye cada factor. Halla los factores comunes de cada par y exclúyelos. Modifica la ecuación apropiadamente.
    • Por ejemplo: x(2x + 5) + 2(2x + 5)
  8. Imagen titulada Factor by Grouping Step 8
    8
    Excluye los paréntesis comunes. Debe haber paréntesis binomiales comunes entre las dos mitades. Exclúyelos y coloca los otros términos en otros paréntesis.
    • Por ejemplo: (2x + 5)(x + 2)
  9. Imagen titulada Factor by Grouping Step 9
    9
    Escribe tu respuesta. Ahora debes tener tu respuesta final.
    • Por ejemplo: 2x2 + 9x + 10 = (2x + 5)(x + 2)
      • La respuesta final es: (2x + 5)(x + 2)

Ejemplos adicionales

  1. Imagen titulada Factor by Grouping Step 10
    1
    Factoriza: 4x2 - 3x - 10
    • a * c = 4 * -10 = -40
    • Factores de 40: (1, 40), (2, 20), (4, 10), (5, 8)
    • Par de factores correcto: (5, 8); 5 - 8 = -3
    • 4x2 - 8x + 5x - 10
    • (4x2 - 8x) + (5x - 10)
    • 4x(x - 2) + 5(x - 2)
    • (x - 2)(4x + 5)
  2. Imagen titulada Factor by Grouping Step 11
    2
    Factoriza: 8x2 + 2x - 3
    • a * c = 8 * -3 = -24
    • Factores de 24: (1, 24), (2, 12), (4, 6)
    • Par de factores correcto: (4, 6); 6 - 4 = 2
    • 8x2 + 6x - 4x - 3
    • (8x2 + 6x) - (4x + 3)
    • 2x(4x + 3) - 1(4x + 3)
    • (4x + 3)(2x - 1)

Método 2
Método 2 de 2:
Polinomios con cuatro términos[2]

  1. Imagen titulada Factor by Grouping Step 12
    1
    Observa la ecuación. La ecuación debe tener cuatro términos separados. Sin embargo, la apariencia exacta de aquellos cuatro términos puede variar.
    • Por lo general, usarás este método cuando tengas una ecuación polinómica que se vea así: ax3 + bx2 + cx + d
    • La ecuación también puede verse así:
      • axy + by + cx + d
      • ax2 + bx + cxy + dy
      • ax4 + bx3 + cx2 + dx
      • O variaciones similares.
    • Por ejemplo: 4x4 + 12x3 + 6x2 + 18x
  2. Imagen titulada Factor by Grouping Step 13
    2
    Excluye el máximo común divisor (MCD). Determina si todos los cuatro términos tienen algo en común. El máximo común divisor de los cuatro términos, si existe algún factor común, se deberá excluir de la ecuación.
    • Si lo único que los cuatro términos tienen en común es el número "1", no hay MCD y nada se puede excluir en este momento.
    • Cuando sí excluyes un MCD, asegúrate de seguir manteniéndolo en la parte delantera de la ecuación mientras trabajas. Este MCD que ha sido excluido se debe incluir como parte de tu respuesta final para que sea correcta.
    • Por ejemplo: 4x4 + 12x3 + 6x2 + 18x
      • Cada término tiene 2x en común, así que el problema se puede reformular de la siguiente forma:
      • 2x(2x3 + 6x2 + 3x + 9)
  3. Imagen titulada Factor by Grouping Step 14
    3
    Crea grupo más pequeños dentro del problema. Agrupa los primeros dos términos y los segundos dos términos.
    • Si el primer término del segundo grupo tiene un signo negativo, deberás poner un signo negativo delante del segundo paréntesis. Deberás cambiar el signo del segundo término de dicho grupo para reflejar esa opción.
    • Por ejemplo: 2x(2x3 + 6x2 + 3x + 9) = 2x[(2x3 + 6x2) + (3x + 9)]
  4. Imagen titulada Factor by Grouping Step 15
    4
    Excluye en MCD de cada binomio. Identifica el MCD en cada par de binomio y factorízalo fuera del par. Modifica la ecuación adecuadamente.
    • A estas alturas, es probable que tengas que elegir entre excluir un número positivo o un número negativo del segundo grupo. Observa los signos antes del segundo y cuarto término.
      • Cuando los dos signos son iguales (ambos positivos o ambos negativos), excluye un número positivo.
      • Cuando los dos signos son diferentes (uno negativo y otro positivo), excluye un número negativo.
    • Por ejemplo: 2x[(2x3 + 6x2) + (3x + 9)] = 2x2[2x2(x + 3) + 3(x + 3)]
  5. Imagen titulada Factor by Grouping Step 16
    5
    Excluye el binomio en común. El par de binomio que está dentro de ambos paréntesis deberá ser igual. Exclúyelos de la ecuación, luego agrupa los términos que quedaron en otros paréntesis.
    • Si los binomios dentro de los paréntesis actuales no son los mismos, revisa nuevamente tu trabajo y trata de ordenar tus términos y agrupar nuevamente la ecuación.
    • Los paréntesis deben coincidir. Si no coinciden, sin importar lo que hagas, el problema no se puede factorizar por agrupación o por algún otro método.
    • Por ejemplo: 2x2[2x2(x + 3) + 3(x + 3)] = 2x2[(x + 3)(2x2 + 3)]
  6. Imagen titulada Factor by Grouping Step 17
    6
    Escribe tu respuesta. En este momento ya debes tener tu respuesta final.
    • Por ejemplo: 4x4 + 12x3 + 6x2 + 18x = 2x2(x + 3)(2x2 + 3)
      • La respuesta final es: 2x2(x + 3)(2x2 + 3)

Ejemplos adicionales

  1. Imagen titulada Factor by Grouping Step 18
    1
    Factoriza: 6x2 + 2xy - 24x - 8y
    • 2[3x2 + xy - 12x - 4y]
    • 2[(3x2 + xy) - (12x + 4y)]
    • 2[x(3x + y) - 4(3x + y)]
    • 2[(3x + y)(x - 4)]
    • 2(3x + y)(x – 4)
  2. Imagen titulada Factor by Grouping Step 19
    2
    Factoriza: x3 - 2x2 + 5x - 10
    • (x3 - 2x2) + (5x - 10)
    • x2(x - 2) + 5(x - 2)
    • (x - 2)(x2 + 5)

wikiHows relacionados

calcular el diámetro de un círculo
Cómo
calcular el diámetro de un círculo
calcular un incremento en porcentaje
Cómo
calcular un incremento en porcentaje
calcular la variación porcentual
Cómo
calcular la variación porcentual
encontrar el valor de X
Cómo
encontrar el valor de X
medir milímetros
Cómo
medir milímetros
calcular una frecuencia
Cómo
calcular una frecuencia
calcular las probabilidades de sacarte la lotería
Cómo
calcular las probabilidades de sacarte la lotería
convertir de grados a radianes
Cómo
convertir de grados a radianes
calcular la varianza
Cómo
calcular la varianza
calcular la incertidumbre
Cómo
calcular la incertidumbre
convertir radianes a grados
Cómo
convertir radianes a grados
calcular la velocidad
Cómo
calcular la velocidad
calcular el porcentaje de error
Cómo
calcular el porcentaje de error
encontrar una raíz cuadrada sin una calculadora
Cómo
encontrar una raíz cuadrada sin una calculadora

Referencias

  1. ↑ http://www.mathwarehouse.com/algebra/polynomial/how-to-factor-by-grouping.php
  2. ↑ http://www.wtamu.edu/academic/anns/mps/math/mathlab/int_algebra/int_alg_tut27_gcf.htm

Acerca de este wikiHow

wikiHow es un "wiki", lo que significa que muchos de nuestros artículos están escritos por varios autores. Para crear este artículo, autores voluntarios han trabajado para editarlo y mejorarlo con el tiempo. Este artículo ha sido visto 10 646 veces.
Categorías: Matemáticas