Nuestro equipo de editores e investigadores capacitados han sido autores de este artículo y lo han validado por su precisión y amplitud.
wikiHow's Content Management Team revisa cuidadosamente el trabajo de nuestro personal editorial para asegurar que cada artículo cumpla con nuestros altos estándares de calidad.
Este artículo ha sido visto 432 098 veces.
Por una serie de razones, es posible que necesites definir el valor máximo o mínimo de una función cuadrática seleccionada. Puedes hallar el máximo o mínimo si la función original está escrita en forma general, , o en forma estándar, . Por último, probablemente también quieras realizar algunos cálculos básicos para definir el máximo o mínimo de cualquier función cuadrática.
Pasos
Método 1
Método 1 de 3:Comenzar con la forma general de la función
-
1Establece la función en forma general. Una función cuadrática es aquella que tiene un término . También existe la posibilidad de que contenga un término sin exponente. Asimismo, no habrá exponentes que sean mayores que 2. La forma general es . De ser necesario, combina los términos semejantes y reorganiza la ecuación para que la función adopte la forma general.[1]
- Por ejemplo, supongamos que comienzas con . Combina los términos y los términos para obtener la siguiente forma general:
- Por ejemplo, supongamos que comienzas con . Combina los términos y los términos para obtener la siguiente forma general:
-
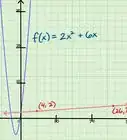
2Determina la dirección del gráfico. Una función cuadrática da origen a una parábola en el gráfico, la cual puede estar orientada hacia arriba o hacia abajo. Si , el coeficiente del término , tiene valor positivo, la parábola estará orientada hacia arriba. Por el contrario, si tiene valor negativo, la parábola estará orientada hacia abajo. Observa los siguientes ejemplos:[2]
- Para , ; por lo tanto, la parábola se orienta hacia arriba.
- Para , ; por lo tanto, la parábola se orienta hacia abajo.
- Para , ; por lo tanto, la parábola se orienta hacia arriba.
- Puedes recordar este concepto pensando en caras sonrientes y ceños fruncidos. Si alguien es positivo, sonríe; mientras que alguien negativo frunce el ceño. De manera similar, un número positivo tendrá una parábola ascendente, mientras que uno negativo tendrá una descendente.
- Si la parábola se orienta hacia arriba, hallarás su valor mínimo, mientras que, si se orienta hacia abajo, hallarás su valor máximo.
-
3Calcula -b/2a. El valor de te indica el valor del vértice de la parábola. Si la función cuadrática está escrita en su forma general de , utiliza los coeficientes de los términos y de la siguiente manera:
- Para una función , y . Por lo tanto, halla el valor de x del vértice de la siguiente manera:
- Como segundo ejemplo, considera la siguiente función: . En este ejemplo, y . Por lo tanto, halla el valor de x del vértice de la siguiente forma:
- Para una función , y . Por lo tanto, halla el valor de x del vértice de la siguiente manera:
-
4Halla el valor de f(x) correspondiente. Introduce el valor de x que acabas de calcular en la función con la finalidad de hallar el valor correspondiente de f(x). Este será el valor mínimo o máximo de la función.
- En el caso del primer ejemplo mostrado previamente, , calculaste el valor de x para que el vértice sea . Reemplaza con en la función para hallar el valor máximo:
- En el caso del segundo ejemplo mostrado previamente, , descubriste que el valor del vértice es . Reemplaza con en la función para hallar el valor máximo:
- En el caso del primer ejemplo mostrado previamente, , calculaste el valor de x para que el vértice sea . Reemplaza con en la función para hallar el valor máximo:
-
5Informa tus resultados. Revisa la pregunta que te han planteado. Si te piden las coordenadas del vértice, necesitarás hallar los valores de tanto como (o ). Si solo te piden el valor máximo o mínimo, lo único que necesitarás indicar es el valor de (o ). Remítete al valor del coeficiente para estar seguro de si tienes un valor máximo o mínimo.
- En el primer ejemplo, , el valor de es positivo, de modo que deberás indicar el valor mínimo. El vértice se encuentra en , y el valor mínimo es .
- En el segundo ejemplo, , el valor de es negativo, de modo que deberás indicar el valor máximo. El vértice se encuentra en , y el valor máximo es .
Anuncio
Método 2
Método 2 de 3:Utilizar la forma estándar o vértice
-
1Escribe la función cuadrática en forma estándar o vértice. La forma estándar de una función cuadrática general, la cual también puede llamarse la forma vértice, se ve de la siguiente manera:[3]
- Si ya te proporcionaron la función en esta forma, solo necesitas reconocer las variables , y . Si, por el contrario, la función comienza en la forma general , tendrás que completar el cuadrado para reescribirla en la forma vértice.
- Si quieres ver cómo completar el cuadrado, lee el artículo “Cómo completar el cuadrado”.
-
2Determina la dirección del gráfico. Como solo una función cuadrática escrita en su forma general, podrás determinar la dirección de la parábola al ver el coeficiente . Si, en esta forma estándar, el coeficiente es positivo, entonces la parábola estará orientada hacia arriba. Si, por el contrario, es negativo, entonces la parábola estará orientada hacia abajo. Presta atención a los siguientes ejemplos:[4]
- Para , , el cual es positivo. Por lo tanto, la parábola se orienta hacia arriba.
- Para , , el cual es negativo. Por lo tanto, la parábola se orienta hacia abajo.
- Si la parábola se orienta hacia arriba, hallarás su valor mínimo. Si la parábola se orienta hacia abajo, hallarás su valor máximo.
-
3Identifica el valor mínimo o máximo. Cuando la función está escrita en la forma estándar, hallar el valor máximo o mínimo será tan simple como establecer el valor de la variable . En el caso de los dos ejemplos mencionados previamente, estos valores son los siguientes:
- Para , . Este es el valor mínimo de la función, pues esta parábola se orienta hacia arriba.
- Para , . Este es el valor máximo de la función, pues esta parábola se orienta hacia abajo.
-
4Halla el vértice. Si te solicitan las coordenadas del valor mínimo o máximo, el punto será . No obstante, ten en cuenta que, en la forma estándar de la ecuación, el término dentro de los paréntesis es , de modo que necesitas el signo opuesto del número que sigue a .
- Para , el término dentro de los paréntesis es (x+1), el cual puede reescribirse como (x-(-1)). De modo que . Por lo tanto, las coordenadas del vértice para esta función son .
- Para , el término dentro de los paréntesis es (x-2). De modo que, . Por lo tanto, las coordenadas del vértice son (2, 2).
Anuncio
Método 3
Método 3 de 3:Utilizar el cálculo para derivar el mínimo o máximo
-
1Comienza con la forma general. Escribe la función cuadrática en la forma general, . De ser necesario, quizás necesites combinar los términos semejantes y reorganizarlos para dar lugar a forma adecuada.[5]
- Comienza con la siguiente función: .
-
2Utiliza la regla de exponentes para hallar la primera derivada. Mediante el uso de cálculos básicos, podrás hallar la primera derivada de la función cuadrática general: .[6]
- En el caso de la función , Halla la derivada de la siguiente manera:
- En el caso de la función , Halla la derivada de la siguiente manera:
-
3Iguala la derivada a cero. Recuerda que la derivada de una función te indica la pendiente que tiene en un punto seleccionado. El mínimo o máximo de una función se produce cuando la pendiente equivale a cero. Por lo tanto, para hallar el punto en que se produce el mínimo o máximo, iguala la derivada a cero. Continúa con el problema utilizado anteriormente a modo de ejemplo:[7]
-
4Halla x. Utiliza álgebra básica para reorganizar la función y hallar el valor de x, cuando la derivada sea igual a cero. Esta solución te indicará la coordenada x del vértice de la función, que es el punto en que se produce el máximo o el mínimo.[8]
-
5Introduce el valor resulto de x en la función original. El valor mínimo o máximo de la función será el valor de en la posición seleccionada. Introduce el valor de en la función original y halla el mínimo o máximo.[9]
- En el caso de la función en ,
- En el caso de la función en ,
-
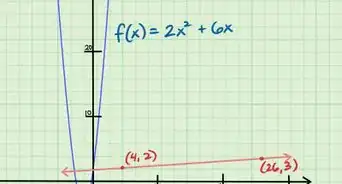
6Indica la solución. La solución indicará el vértice del punto máximo o mínimo. En el caso de esta función , el vértice estará en . El coeficiente es positivo, de modo que la función está orientada hacia arriba. Por lo tanto, el valor mínimo de la función es la coordenada y del vértice, la cual es .[10]Anuncio
Consejos
- El eje de simetría de la parábola es x = h.
Referencias
- ↑ http://www.analyzemath.com/quadraticg/quadraticg.htm
- ↑ http://www.personal.kent.edu/~bosikiew/Algebra-handouts/quad-extval.pdf
- ↑ http://www.personal.kent.edu/~bosikiew/Algebra-handouts/quad-extval.pdf
- ↑ http://www.personal.kent.edu/~bosikiew/Algebra-handouts/quad-extval.pdf
- ↑ http://www.themathpage.com/acalc/max.htm
- ↑ http://www.themathpage.com/acalc/max.htm
- ↑ http://www.themathpage.com/acalc/max.htm
- ↑ http://www.themathpage.com/acalc/max.htm
- ↑ http://www.themathpage.com/acalc/max.htm






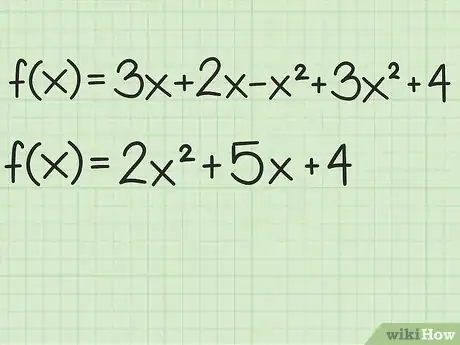



























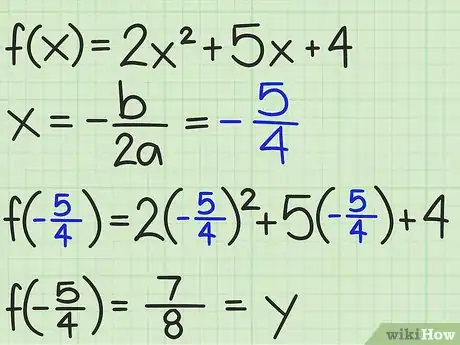















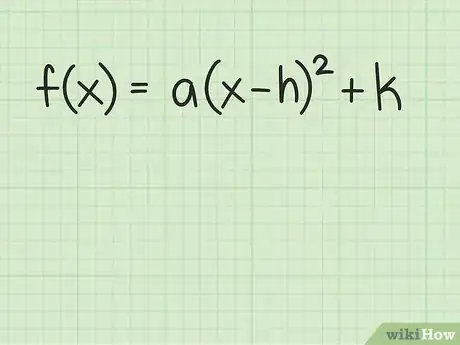














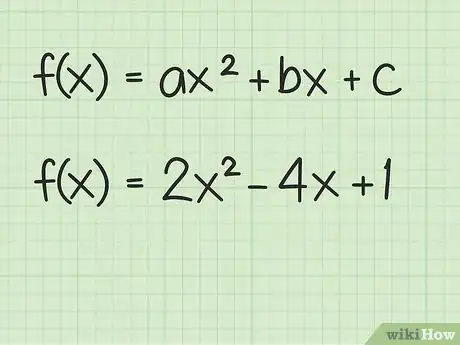

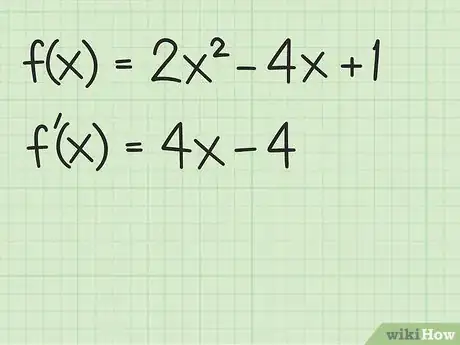


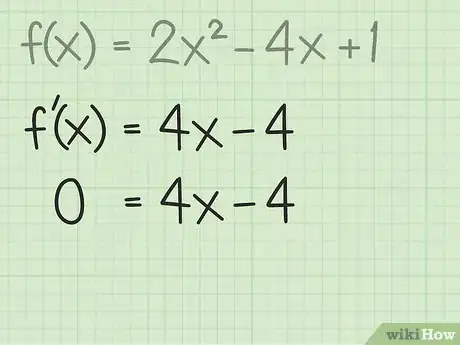




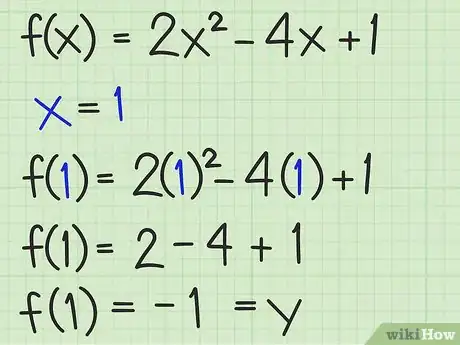







-Step-31-Version-2.webp)
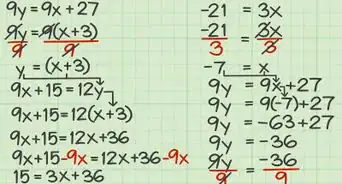



wikiHow's Content Management Team revisa cuidadosamente el trabajo de nuestro personal editorial para asegurar que cada artículo cumpla con nuestros altos estándares de calidad. Este artículo ha sido visto 432 098 veces.