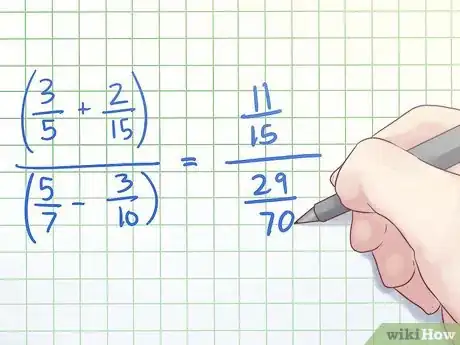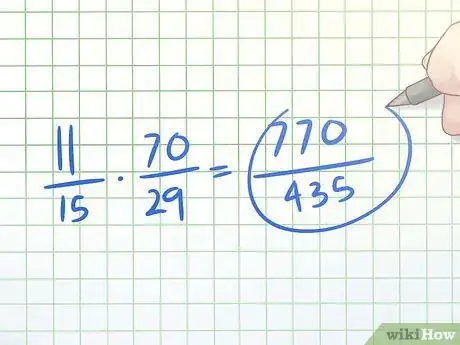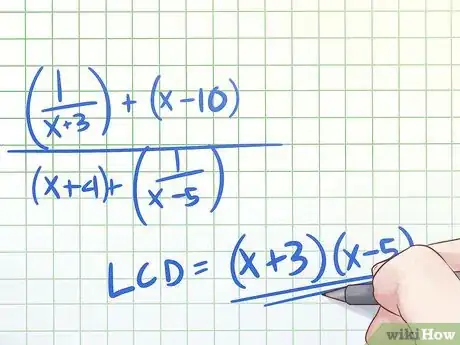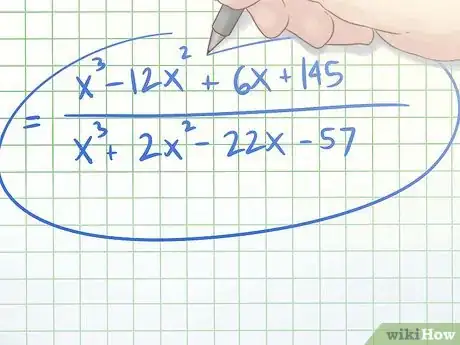Cómo simplificar fracciones complejas

Las fracciones complejas son fracciones en las que el numerador, el denominador o ambos términos contienen fracciones a su vez. Por este motivo, hay quien las llama "fracciones compuestas". Simplificar fracciones complejas es un proceso que puede ser sencillo o difícil, en base al número de términos que haya en el numerador y en el denominador, a que haya términos variables o no y, si los hay, a la complejidad de los términos variables. Lee el paso 1 para empezar.

Método 1

Método 1 de 2:
Simplificar fracciones complejas con el inverso multiplicativo

1
Si es necesario, simplifica el numerador y el denominador para que haya una sola fracción en cada término. Las fracciones complejas no tienen por qué resultar difíciles de resolver. De hecho, las fracciones complejas en las que tanto el numerador como el denominador contienen una sola fracción suelen ser bastante fáciles de resolver. Por lo tanto, si el numerador o el denominador de la fracción compleja (o ambos términos) contienen varias fracciones o una combinación de fracciones y números enteros, simplifica el término para que quede una sola fracción tanto en el numerador como en el denominador. Puede que tengas que hallar el mínimo común denominador (MCD) de dos o más fracciones.
- Por ejemplo, supongamos que queremos simplificar la fracción compleja (3/5 + 2/15)/(5/7 - 3/10). Primero, simplificaríamos tanto el numerador como el denominador de la fracción compleja para que quede una sola fracción en cada término.
  - Para simplificar el numerador, utilizaremos u MCD de 15 multiplicando 3/5 por 3/3. El numerador se convertirá en 9/15 + 2/15 y, después de operar, en 11/15.
  - Para simplificar el denominador, utilizaremos un MCD de 70 multiplicando 5/7 por 10/10 y 3/10 por 7/7. El denominador se transformará en 50/70 - 21/70 y, después de operar, en 29/70.
  - Por lo tanto, la nueva fracción compleja será (11/15)/(29/70).
2
Invierte el denominador para hallar su inverso. Por definición, dividir un número entre otro es lo mismo que multiplicar el primer número por el inverso del segundo. Ahora que ya hemos obtenido una fracción compleja con una sola fracción tanto en el numerador como en el denominador, podemos utilizar esta propiedad de la división para simplificar la fracción compleja. Primero, halla el inverso de la fracción del denominador de la fracción compleja. Hazlo invirtiendo la fracción; es decir, colocando el numerador en lugar del denominador y viceversa.
- En el ejemplo con el que estamos trabajando, la fracción del denominador de la fracción compleja (11/15)/(29/70) es 29/70. Para hallar su inverso, simplemente le "damos la vuelta", obteniendo 70/29.
  - Ten en cuenta que, si la fracción compleja tiene un número entero en el denominador, puedes expresarlo como una fracción y hallar su inverso de la misma forma. Por ejemplo, si la fracción compleja fuese (11/15)/(29), podemos definir el denominador como 29/1, cuyo inverso sería 1/29.
3
Multiplica el numerador de la fracción compleja por el inverso del denominador. Ahora que ya has obtenido el inverso del denominador de la fracción compleja, multiplícalo por el numerador para obtener una sola fracción simple. Recuerda que para multiplicar dos fracciones, simplemente hay que multiplicar los términos (el numerador de la nueva fracción es el producto de los numeradores de las dos antiguas, y lo mismo sucede con el denominador).
- En el ejemplo que hemos puesto, multiplicaríamos 11/15 × 70/29. 70 × 11 = 770 y 15 × 29 = 435. Por lo tanto, la nueva fracción simple será 770/435.
4
Simplifica la nueva fracción hallando el máximo factor común. Ahora tenemos una sola fracción simple, por lo que lo único que queda por hacer es expresar los términos de la forma más sencilla. Halla el máximo factor común (MFC) del numerador y del denominador, y divide ambos términos por este número para simplificar la fracción.
- Un factor común de 770 y 435 es 5. Por lo tanto, si dividimos el numerador y el denominador de la fracción entre 5, obtendremos 154/87. 154 y 87 no tienen ningún factor común, ¡así que ya hemos dado con el resultado final!

Método 2

Método 2 de 2:
Simplificar fracciones complejas con términos variables

1
Siempre que sea posible, utiliza el método del inverso multiplicativo explicado arriba. Para ser claros, prácticamente cualquier fracción compleja se puede simplificar reduciendo su numerador y su denominador a fracciones simples y multiplicando el numerador por el inverso del denominador. Las fracciones complejas con variables no son una excepción, aunque cuanto más complicadas sean las expresiones variables, más difícil será utilizar el inverso multiplicativo y más tiempo llevará. Para resolver fracciones complejas "sencillas" con variables, usar el inverso multiplicativo es una buena opción, pero para resolver las fracciones complejas con varias variables en el numerador y en el denominador puede que sea más fácil usar el método que describiremos a continuación.
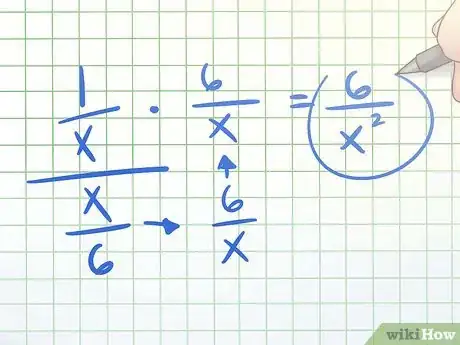
- Por ejemplo, (1/x)/(x/6) es fácil de simplificar con el inverso multiplicativo. 1/x × 6/x = 6/x². Aquí, no hay necesidad de utilizar ningún método alternativo.
- Sin embargo, (((1)/(x+3)) + x - 10)/(x +4 +((1)/(x - 5))) es más difícil de simplificar con el inverso multiplicativo. Reducir el numerador y el denominador de esta fracción compleja para que quede una sola fracción en cada término, multiplicar por el inverso y reducir el resultado a una expresión lo más sencilla posible sería un proceso bastante complicado. En este caso, puede ser más fácil usar el método alternativo que ahora explicaremos.
2
Si no es práctico usar el método del inverso multiplicativo, empieza hallando el mínimo común denominador de las fracciones de cada término de la fracción compleja. El primer paso en este método alternativo de simplificación es hallar el MCD de todas las fracciones que haya en los términos de la fracción compleja (tanto en el numerador como en el denominador. Normalmente, si una o varias fracciones tienen variables en sus denominadores, su MCD es simplemente el producto de sus denominadores.
- Esto es más fácil de comprender a través de un ejemplo. Intentemos simplificar la fracción compleja que hemos mencionado antes, (((1)/(x+3)) + x - 10)/(x +4 +((1)/(x - 5))). Las fracciones de los términos de la fracción compleja son (1)/(x+3) y (1)/(x-5). El denominador común de estas dos fracciones es el producto de sus denominadores: (x+3)(x-5).
3
Multiplica el numerador de la fracción compleja por el MCD que acabas de hallar. Después, necesitaremos multiplicar los términos de la fracción compleja por el MCD de los números fraccionarios del numerador y del denominador. En otras palabras, multiplicaremos la fracción compleja al completo por (MCD)/(MCD). Podemos hacer esto fácilmente porque (LCD)/(LCD) es igual a 1. Primero, multiplica el numerador por sí mismo.
- En el ejemplo, multiplicaríamos la fracción compleja, (((1)/(x+3)) + x - 10)/(x +4 +((1)/(x - 5))), por ((x+3)(x-5))/((x+3)(x-5)). Tendremos que multiplicar el numerador y el denominador de la fracción compleja por (x+3)(x-5).
  - Primero, multipliquemos el numerador: (((1)/(x+3)) + x - 10) × (x+3)(x-5)
    - = (((x+3)(x-5)/(x+3)) + x((x+3)(x-5)) - 10((x+3)(x-5))
    - = (x-5) + (x(x² - 2x - 15)) - (10(x² - 2x - 15))
    - = (x-5) + (x³ - 2x² - 15x) - (10x² - 20x - 150)
    - = (x-5) + x³ - 12x² + 5x + 150
    - = x³ - 12x² + 6x + 145
4
Multiplica el denominador de la fracción compleja por el MCD, tal y como lo has hecho con el numerador. Continúa multiplicando la fracción compleja por el MCD que has hallado, siguiendo con el denominador. Multiplica cada término por el MCD.
- El denominador de la fracción compleja, (((1)/(x+3)) + x - 10)/(x +4 +((1)/(x - 5))), es x +4 +((1)/(x-5)). Lo multiplicaremos por el MCD que hemos hallado, (x+3)(x-5).
  - (x +4 +((1)/(x - 5))) × (x+3)(x-5)
  - = x((x+3)(x-5)) + 4((x+3)(x-5)) + (1/(x-5))(x+3)(x-5).
  - = x(x² - 2x - 15) + 4(x² - 2x - 15) + ((x+3)(x-5))/(x-5)
  - = x³ - 2x² - 15x + 4x² - 8x - 60 + (x+3)
  - = x³ + 2x² - 23x - 60 + (x+3)
  - = x³ + 2x² - 22x - 57
5
Obtén una fracción nueva y simplificada a partir del numerador y del denominador que acabas de hallar. Después de multiplicar la fracción por la expresión (MCD/MCD) y de simplificarla combinando los términos, deberías obtener una fracción simple sin números fraccionarios. Como probablemente hayas notado, multiplicando el MCD de los términos fraccionarios pertenecientes a la fracción compleja, los denominadores de estas fracciones se anulan, dejando términos variables y números enteros en el numerador y en el denominador del resultado, pero ninguna fracción.
- Utilizando el numerador y el denominador que hemos hallado, podemos construir una fracción equivalente a la fracción compleja inicial pero sin términos fraccionarios. El numerador obtenido es x³ - 12x² + 6x + 145, y el denominador es x³ + 2x² - 22x - 57, por lo que la nueva fracción es (x³ - 12x² + 6x + 145)/(x³ + 2x² - 22x - 57)

Consejos

Anota cada paso del proceso. Las fracciones pueden tornarse confusas fácilmente si intentas resolverlas demasiado rápido o de cabeza.
Busca ejemplos de fracciones complejas en internet o en tu libro de texto. Sigue cada paso hasta que entiendas el proceso.