Cet article a été rédigé avec la collaboration de nos éditeurs(trices) et chercheurs(euses) qualifiés(es) pour garantir l'exactitude et l'exhaustivité du contenu.
L'équipe de gestion du contenu de wikiHow examine soigneusement le travail de l'équipe éditoriale afin de s'assurer que chaque article est en conformité avec nos standards de haute qualité.
Cet article a été consulté 19 490 fois.
Les factorielles sont des objets mathématiques peu fréquents, mais très utiles pour ceux qui travaillent dans le domaine des probabilités et de l’algèbre combinatoire (permutations [1] ). Une factorielle se présente sous la forme d’un nombre (n) suivi d’un point d’exclamation (). Cette expression a pour valeur le produit de tous les nombres inférieurs à ce nombre, lui compris. Une fois cette définition acquise, il est très facile avec une calculatrice scientifique de calculer des factorielles.
Étapes
Méthode 1
Méthode 1 sur 3:Calculer des factorielles
-
1Sachez comment se note une factorielle. Une factorielle s’écrit sous la forme d’un nombre simplement suivi d’un point d’exclamation.
- Ainsi, la factorielle se dit « factorielle de 5 » ou « factorielle 5 ».
-
2Inscrivez la séquence de calcul sous-jacente à la factorielle. Il s’agit du produit de tous les nombres, en commençant par celui de la factorielle, inférieurs à ce nombre jusqu’à 1 [2] . De façon théorique, la formule s’écrit comme suit : , étant obligatoirement un entier positif [3] .
- Dans notre exemple, la décomposition est la suivante : . Simplification faite, l’expression est la suivante : .
-
3Faites le produit. Avec une calculatrice scientifique, c’est simple, puisque vous tapez la factorielle et vous appuyez sur la touche . Pour un calcul de tête, essayez de combiner les valeurs pour parfois obtenir 10 ou 100, ce qui facilite les calculs [4] . Quant au 1 final, vous pouvez le négliger, 1 étant neutre pour le produit (il n’en change pas le résultat).
- En calculant , laissez d’ores et déjà tomber la multiplication par le 1 final et faites . Il ne vous reste plus qu’à multiplier . Comme , vous pouvez écrire que :
.
Publicité - En calculant , laissez d’ores et déjà tomber la multiplication par le 1 final et faites . Il ne vous reste plus qu’à multiplier . Comme , vous pouvez écrire que :
Méthode 2
Méthode 2 sur 3:Simplifier une fraction contenant des factorielles
-
1Observez bien l’expression que vous devez simplifier. Le plus souvent, il s’agit d’une expression ayant des factorielles en numérateur et en dénominateur.
- Prenons un exemple concret, simplifions .
-
2Décomposez chaque factorielle. Le but de l’opération est de faire apparaitre des facteurs qui vont s’annuler de part et d’autre du trait de fraction [5] . Au début, vous écrirez tous les facteurs, plus tard, vous irez plus vite en annulant directement telle ou telle factorielle [6] .
- Reprenons notre exemple : . Cette fraction peut être présentée ainsi :
.
- Reprenons notre exemple : . Cette fraction peut être présentée ainsi :
-
3Supprimez tous les facteurs communs. Ils doivent être à la fois en numérateur et en dénominateur [7] . Il vous restera alors une fraction irréductible dont vous calculerez les termes.
- À l’évidence est facteur de , vous pouvez donc supprimer ce qui correspond à en numérateur (il reste ) et en dénominateur :
.
- À l’évidence est facteur de , vous pouvez donc supprimer ce qui correspond à en numérateur (il reste ) et en dénominateur :
-
4Faites les calculs. Cela fait, voyez s’il n’y a pas de simplifications possibles. Le résultat doit toujours être donné sous forme de fraction irréductible.
- Reprenons l’exemple :
.
Ainsi, devient .
Publicité - Reprenons l’exemple :
Méthode 3
Méthode 3 sur 3:Résoudre des problèmes de factorielles
-
1Trouvez la valeur de 8!.
- Sur une calculatrice scientifique, tapez sur la touche , puis sur la touche . Le résultat s’affiche.
- Pour une résolution à la main, écrivez la décomposition de la factorielle :
. - Supprimez le dernier terme (égal à 1) :
. - Mettez en tête de produit :
. - Groupez les autres facteurs par paires pour accélérer les opérations, puis multipliez tous les résultats intermédiaires :
.
Pour résumer, .
-
2Simplifiez l’expression : .
- Décomposez toutes les factorielles :
. - Supprimez terme à terme tout ce qui est commun au numérateur et au dénominateur :
. - Faites les calculs :
.
Ainsi la fraction peut s’écrire sous la forme .
- Décomposez toutes les factorielles :
-
3Résolvez un problème concret. Supposons que vous vouliez repeindre un mur sur lequel il y aura, une fois terminé, 6 bandes de 6 couleurs différentes. Question : Quelles sont les différentes combinaisons possibles ?
- La réponse à ce problème est , nous ne le démontrerons pas ici, mais intuitivement vous pouvez comprendre comment cette solution apparait.
- Pour la première bande, vous avez le choix entre 6 couleurs. Pour la suivante, vous n’avez que 5 choix possibles, etc. C’est comme cela que les choix sont :
. Ce produit est . - Sur une calculatrice scientifique, tapez , puis appuyez tout simplement sur la touche .
- Pour une résolution sur le papier, écrivez le produit :
. - Négligez le 1 final :
. - Groupez en tête de produit :
. - Groupez les autres facteurs par paires pour accélérer les opérations, puis multipliez tous les résultats intermédiaires :
.
Il y a 720 combinaisons possibles de bandes de 6 couleurs différentes.
-
4Résolvez un autre problème concret. Il est assez proche du précédent dans la mesure où vous avez toujours un mur et 6 couleurs à disposition. La différence tient au fait que vous n’allez faire que trois bandes de trois couleurs différentes. Question : Quelles sont les différentes combinaisons possibles ?
- De façon simple, vous pouvez dire que vous avez 6 choix pour la première bande, 5 pour la suivante et 4 pour la dernière, c’est-à-dire la première partie de factorielle 6. Cependant, sachez qu’il existe, pour ce genre de calcul combinatoire, une formule toute prête : , étant le nombre d’éléments à disposition au départ et le nombre d’éléments réellement choisis parmi les n éléments. Cette formule n’est utilisable qu’aux conditions expresses qu’il n’y ait pas de répétitions (dans notre exemple, une même couleur qui serait choisie deux fois) et qu’il y ait une séquence ordonnée de choix possibles [8] .
- Ainsi, dans notre exemple de trois bandes de trois couleurs différentes prises parmi 6 possibles, le nombre de combinaisons possibles s’établit comme suit :
. - Faites la seule soustraction en dénominateur :
. - Décomposez chacune des deux factorielles :
. - Supprimez tous les facteurs communs au numérateur et au dénominateur :
. - Faites les calculs restants : .
Avec 6 couleurs disponibles, vous avec 120 combinaisons possibles pour faire 3 bandes de couleur sur votre mur.
Publicité
Conseils
- Il est une factorielle spéciale : c’est 1! dont la valeur est… 1!.
- Par convention, qui semble un peu illogique eu égard à la définition, il a été établi que 0! = 1.
- Les factorielles sont très utiles en théorie des nombres et des probabilités. Entrainez-vous !
- Comme dans tout exercice d’algèbre, vérifiez toujours vos résultats.
Références
- ↑ https://www.mathsisfun.com/combinatorics/combinations-permutations.html
- ↑ https://www.mathsisfun.com/numbers/factorial.html
- ↑ http://mathworld.wolfram.com/Factorial.html
- ↑ https://godiche.ru/education-et-langues/math/algbre/17812-comment-simplifier-les-expressions-factoriels.html
- ↑ https://godiche.ru/education-et-langues/math/algbre/17812-comment-simplifier-les-expressions-factoriels.html
- ↑ https://godiche.ru/education-et-langues/math/algbre/17812-comment-simplifier-les-expressions-factoriels.html
- ↑ http://www.purplemath.com/modules/factorial.htm
- ↑ https://www.mathsisfun.com/combinatorics/combinations-permutations.html



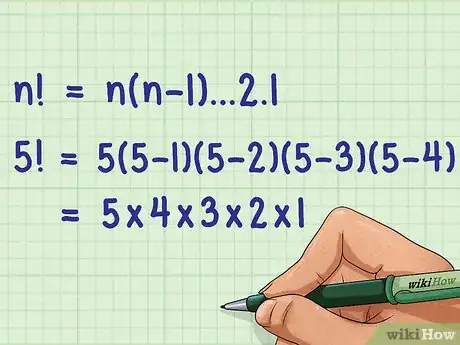




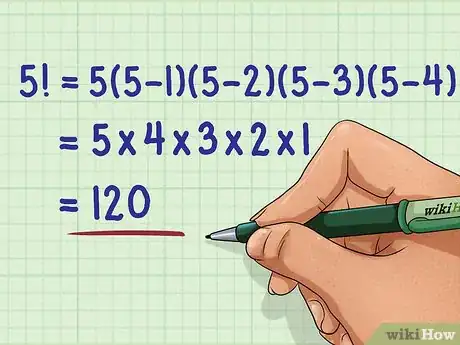





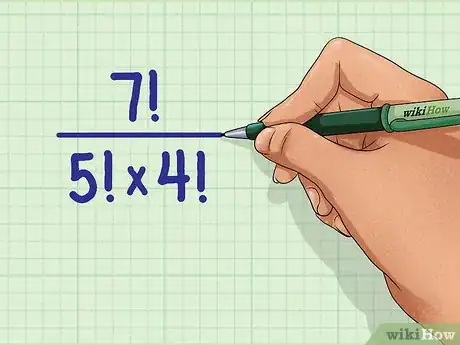



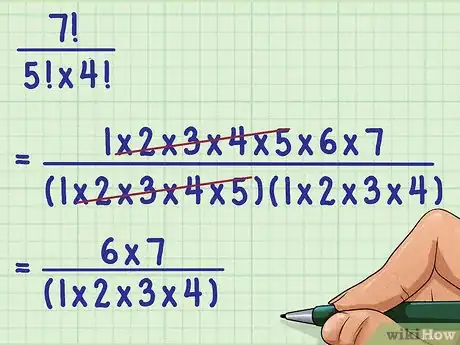



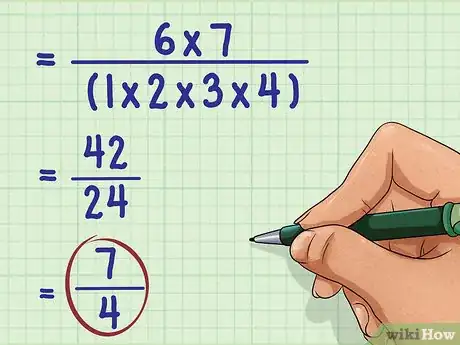


























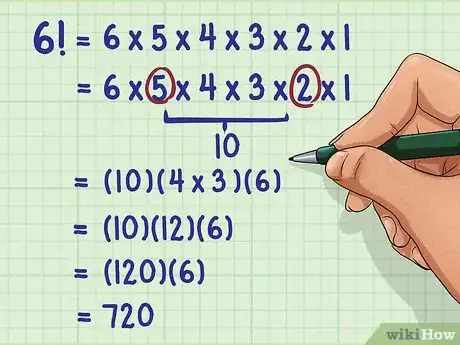




























L'équipe de gestion du contenu de wikiHow examine soigneusement le travail de l'équipe éditoriale afin de s'assurer que chaque article est en conformité avec nos standards de haute qualité. Cet article a été consulté 19 490 fois.