Comment déterminer un rapport de transmission

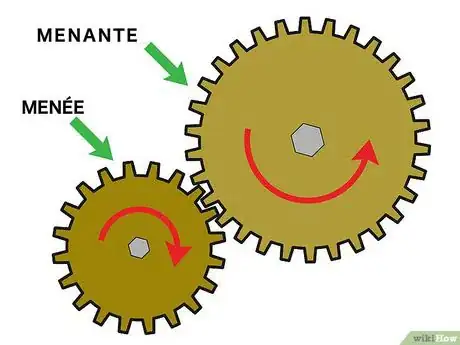
En mécanique, une transmission de mouvement s'effectue fréquemment par le biais d'engrenages, des roues dentées encastrées les unes dans les autres, ce qui transmet le mouvement, mais modifie les vitesses de rotation des roues. Dans un engrenage, il y a toujours une roue motrice (menante), et une ou plusieurs roues entrainées (menées). Rarement, ces roues sont d'un même diamètre si bien que les vitesses de rotation des roues sont différentes. Selon le rapport de taille qui existe entre les deux roues, avec une certaine vitesse de la roue menante, vous aurez une réduction ou une augmentation de la vitesse de rotation de la roue menée. Ce rapport ou raison ( $r$ ) a pour formule : $r={\frac {nombre\ de\ dents\ roue\ menante}{nombre\ de\ dents\ roue\ men{\acute {e}}e}}$ .

Méthode 1

Méthode 1 sur 2:
Trouver le rapport de transmission d'un train d'engrenages

Train à deux roues

1
Comprenez bien ce qu'est un engrenage. Pour faire simple, nous prendrons simplement deux roues, l'ensemble s'appelle un train d'engrenages. Ces roues sont solidaires d'arbres qui vont tourner. Une des roues tourne, c'est la roue menante, tandis que la seconde est la roue menée. Le phénomène est exactement le même quand il y a plusieurs engrenages, les pignons intermédiaires sont dits « fous ». Ce qui change d'une roue à l'autre, ce sont les sens et les vitesses de rotation ^{[1]
X
Source de recherche}.
- Partons d'un exemple concret comme sur l'illustration ci-dessus. Deux roues, l'une grande, l'autre petite, s'encastrent parfaitement et ici, la grande roue entraine la petite. Les choses étant posées, il est possible, moyennant certaines informations, de calculer la raison, c'est-à-dire le rapport de transmission existant entre les 2 roues.
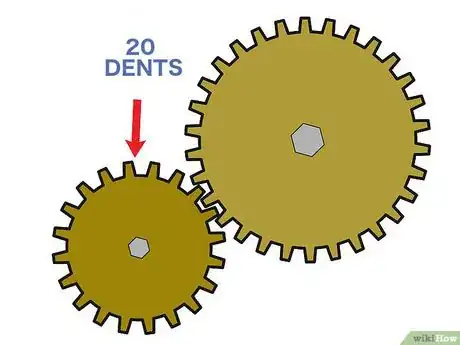
2
Comptez le nombre de dents de la roue menée. Pour calculer la raison d'un tel système, soit le rapport de réduction ou de multiplication, comptez le nombre de dents (crêtes situées en périphérie) de ces roues. Commencez par compter le nombre de dents de la roue menée sans vous tromper, peut-être ce nombre est-il marqué sur la roue ou dans la notice du système ^{[2]
X
Source de recherche}.
- Sur l'illustration, vous avez une roue dentée faite de 20 dents, nous l'appellerons la petite roue.
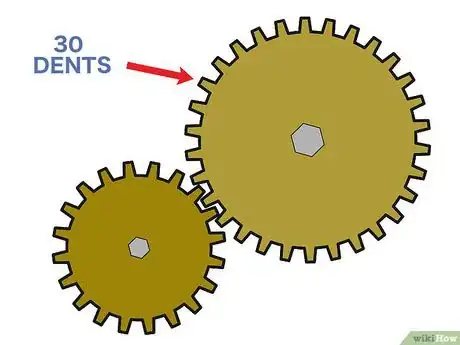
3
Comptez le nombre de dents de la roue menante. Pour le calcul de la raison, l'étape suivante consiste à compter précisément combien il y a de dents sur la roue menante, comme cela a été fait précédemment pour la roue menée.
- Sur l'illustration, vous avez une roue dentée faite de 30 dents, nous l'appellerons la grande roue.
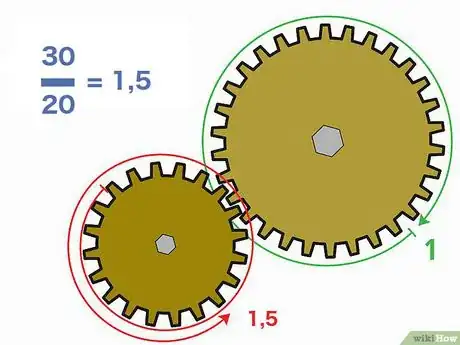
4
Divisez les nombres de dents. Maintenant que vous avez les deux nombres de dents, vous êtes en mesure de trouver facilement le rapport de transmission $r$ $r$ . Il s'agit de ne pas diviser n'importe comment : il faut diviser le nombre de dents de la roue menante par celui de la roue menée. Le résultat obtenu, qui n'a pas d'unité, peut être donné de 3 façons : sous forme fractionnaire, décimale ou de rapport (x : y ^{[3]
X
Source de recherche}).
- Pour reprendre notre exemple, divisons les 30 dents de la roue menante par les 20 dents de la roue menée et nous obtenons : $r={\frac {30}{20}}=1,5$ , ce qui peut aussi s'écrire $r={\frac {3}{2}}$ ou $1,5:1$ .
- Cette raison de 1,5 signifie que lorsque la roue menante (la grande) fait un tour, la roue menée (la petite) fait un tour et demi : c'est ce que l'on appelle un rapport de multiplication.
Publicité

Train à roues multiples

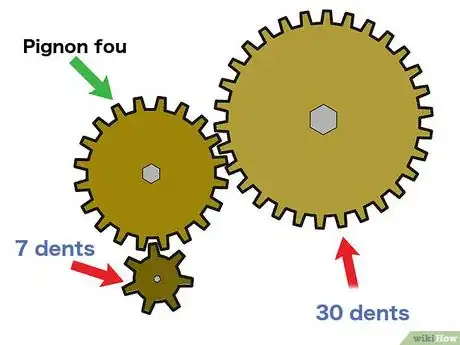
1
Envisagez un train de plusieurs deux roues. Comme son nom l'indique, « un train d'engrenages » est composé de plusieurs engrenages et non pas seulement une roue menante et une roue menée. Dans ce cas de figure, la première roue reste la roue menante et c'est la dernière du train qui est la roue menée. Les engrenages intermédiaires sont soit des pignons « fous ». Ces derniers servent soit à inverser le sens de rotation soit à relier deux axes distants soit à connecter deux pignons qui, sans ce dispositif, ne pourraient pas fonctionner ^{[4]
X
Source de recherche}.
- Prenons comme exemple concret un train d'engrenages comprenant à une extrémité une grande roue menante de 30 dents, une petite roue menée de 7 dents à l'autre extrémité et entre les deux, un pignon fou de 20 dents.
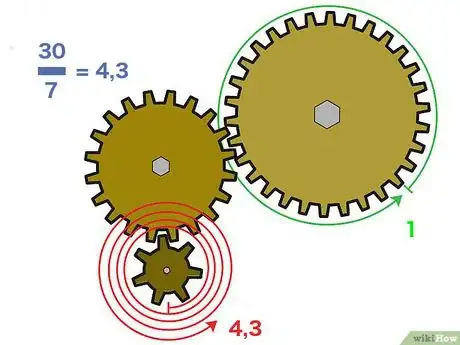
2
Divisez le nombre de dents de la roue menante par celui de la menée. Aussi bizarre que cela paraisse, avec un train d'engrenages de plus de deux pignons, seules comptent la roue menante et la roue menée (le plus souvent, ce seront la première et la dernière). Exprimé autrement : les pignons intermédiaires n'affectent en rien le rapport de transmission général du train. Vous avez votre roue menante et votre roue menée, vous pouvez calculer le rapport de transmission comme cela a été fait précédemment.
- Dans l'exemple choisi, nous allons diviser les 30 dents de la roue menante par les 7 dents de la roue menée. On obtient une raison du train de : 30/7, soit environ 4,3 (ou encore 4,3:1). Concrètement, quand la grande fait 1 tour, la petite en fait 4,3.
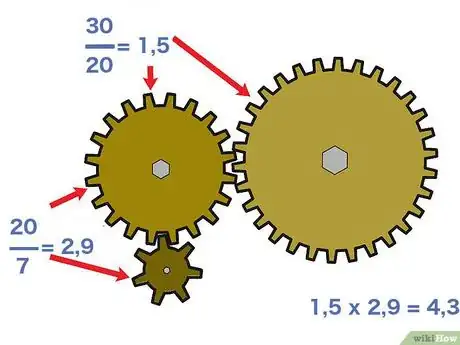
3
Calculez éventuellement les raisons intermédiaires. Au besoin, vous pouvez calculer les rapports de transmission intermédiaires, entre deux roues consécutives ou non, du train. Commencez par le calcul de la raison entre la roue menante et la roue suivante (le pignon fou). Poursuivez avec le calcul par la raison entre le pignon fou et la roue menée. Bien évidemment, si le train comprenait plus de liaisons, il faudrait, sur le même principe, poursuivre les calculs des raisons successives.
- Avec notre exemple, les raisons de trains sont les suivants : 20/7 = 2,9 (première et deuxième roues) et de 30/20 = 1,5 (deuxième et troisième roues). Pour l'instant, rien qui ressemble de près ou de loin à la valeur 4,3 trouvée !
- Cependant, si l'on fait le produit de 20/7 par 30/20, on obtient… 4,3. Une seule conclusion s'impose : le rapport de transmission général est égal au produit des rapports de transmission intermédiaires.
Publicité

Méthode 2

Méthode 2 sur 2:
Calculer une vitesse de rotation avec une raison de train

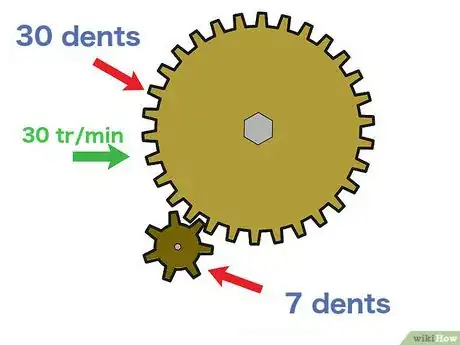
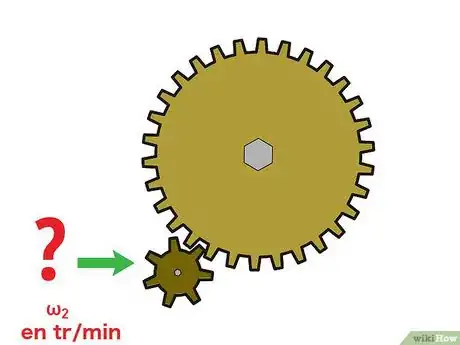
1
Trouvez la vitesse de rotation de votre roue menante. Partant du concept de rapport de transmission, il est possible de calculer la vitesse d'une roue menée dès lors que l'on connait la vitesse « d'entrée », celle de la roue menante. En premier, récupérez la vitesse de rotation de la roue menante. Le plus souvent souvent, elle est donnée en tours par minute (tr/min), d'autres unités sont possibles ^{[5]
X
Source de recherche}.
- Prenons comme exemple un train d'engrenages avec une roue menante de 30 dents tournant à 30 tr/min et une roue menée de 7 dents. Avec toutes ces informations, il est possible de calculer facilement la vitesse de la roue menée.
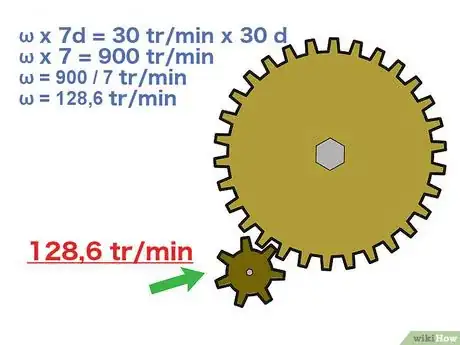
2
Faites l'application numérique. La formule à utiliser est la suivante :
$\omega _{1}\times Z_{1}=\omega _{2}\times Z_{2}$ $\omega _{1}\times Z_{1}=\omega _{2}\times Z_{2}$ , avec $\omega _{1}$ $\omega _{1}$ la vitesse de rotation de la roue menante, $Z_{1}$ $Z_{1}$ le nombre de dents de cette même roue, $\omega _{2}$ $\omega _{2}$ et $Z_{2}$ $Z_{2}$ étant respectivement la vitesse de rotation et le nombre de dents de la roue menée. Chacune de ces données peut être calculée si vous avez les trois autres.
- Le plus souvent, c'est la vitesse $\omega _{2}$ , la vitesse de sortie, qu'on cherche. Rien n'empêche d'avoir à calculer une autre de ces variables. Dans notre exemple, nous allons remplacer $\omega _{2}$ par $\omega$ , il n'y a qu'une inconnue.
- L'équation se présente ainsi : $30\ tr/min\times 30\ d=\omega \times 7\ d$ que nous écrirons $\omega \times 7\ d=30\ tr/min\times 30\ d$ .
3
Faites les calculs. Trouver $\omega$ $\omega$ passe par un simple calcul algébrique qui va consister, comme d'habitude, à isoler l'inconnue qu'on cherche. Pour un exercice noté, vous ferez attention aux unités, sans quoi vous allez perdre des points.
- Voici comment on procède :
- $\omega \times 7\ d=30\ tr/min\times 30\ d$
- $\omega \times 7=30\ tr/min\times 30$ ( $d$ se simplifie de chaque côté)
- $\omega =900/7\ tr/min$
- $\omega =128,6\ tr/min$
- Dit autrement, si la roue menante tournait à 30 tr/min, la roue menée tournerait à 128,6 tr/min. La logique est respectée : la grande roue fait tourner plus vite la petite dans une proportion qui n'est rien d'autre que la raison du train, un rapport de multiplication.
Publicité

Conseils

Sur une voiture par exemple, la puissance nécessaire pour entrainer le système de roulement est conditionnée par la démultiplication (ou la réduction) appliquée à la puissance issue du moteur conformément au rapport de transmission. Le régime du moteur doit être adapté à la puissance demandée par le système de roulement, c'est pourquoi on change de vitesse, en fait de rapport de transmission. La démultiplication (l'arbre de sortie de boite tourne plus vite que l'arbre primaire) nécessite un moteur qui délivre sa puissance optimale à bas régime.
Pour bien comprendre cette notion de rapport de transmission, prenons l'exemple d'une balade en VTT. Vous avez surement remarqué que dans les côtes, vous avancez plus facilement si vous mettez le petit plateau à l’avant et un grand pignon à l'arrière. Vous allez mouliner sans forcer, car le rapport de transmission est proche de 1. Vous avancez moins vite que sur le plat, portion sur laquelle on met généralement le grand plateau à l'avant et un petit pignon à l'arrière. On a alors à chaque tour de pédale un grand développement.
D'un autre côté, la réduction (l'arbre de sortie de boite tourne moins vite que l'arbre primaire) nécessite un moteur qui délivre sa puissance optimale à haut régime.