ثقب أسود دوار

الثقب الأسود الدوار هو ثقب أسود يملك زخم زاوي أي دوران حول نفسه، وبشكل أدق فهو يدور حول أحد محاوره التناظرية.(1)

صورة تبين تأثير الدوران على ثقب أسود ستاتيكي (ثقب أسود شفارزتشيلد)، حيث تمثل قيمة المعامل "a" نسبة الزخم الزاوي للثقب الأسود إلى كتلته، في حالة "a=0" يكون الثقب عديم الدوران، ويكون في اقصى دوران له عندما "a=1"، المنطقة الخارجية لافق الحدث في حالة الدوران تسمى منطقة الإرغوسفير.


أنواع الثقوب السوداء

توجد هناك أربعة حلول معروفة تمثل مجالات الجاذبية القوية في معادلات حقل أينشتاين التي تصف الجاذبية في النظرية النسبية العامة، تسمى نتائجها بالثقوب السوداء اثنان من هذه الحلول والتي هي حل «ثقب أسود كير» و «ثقب أسود كير-نيومان» يتناولان ثقب أسود يدور حول نفسه.

بشكل عام أن كل ثقب أسود في الكون يتحول بسرعة إلى الحالة المستقرة، ومن خلال نظرية اللا-شعر، يمكن أن توصف الثقوب السوداء المستقرة في أية حالة أو لحظة زمنية بهذه الاعداد الإحدى عشر (باستثناء الحالات الكمية):

صورة تبين تأثير "سحب الإطار المرجعي" حول الثقب الأسود، والتي تجعل أي جسم يقترب من منطقة الإرغوسفير يسلك مسار دائري بنفس اتجاه دوران الثقب الأسود حول نفسه، مهما كانت سرعته الابتدائية أو اتجاه حركته.


توضح هذه الصورة المدار الذي قد يسلكه أي جسم يدور حول الثقب الأسود، حيث أن تأثير دوران الثقب الكبير المحدث لتأثير "سحب الإطار المرجعي" يمنع الجسم من أن يسلك مدار منتظم حول الثقب الأسود.

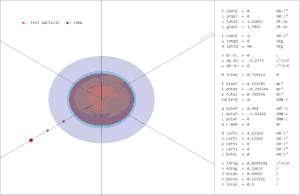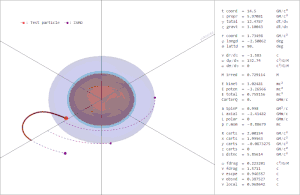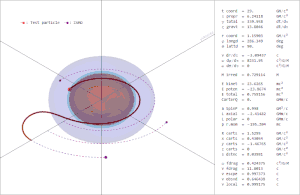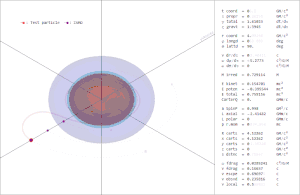
تمثل هذه الأعداد صفات الثقب الأسود التي يمكن تحديدها بواسطة اختبار حقله الكهرومغناطيسي ومجال الجاذبية الخاص به، جميع الصفات الأخرى في الثقب الأسود إما أن تفلت إلى المالانهاية أو أن يبتلعها الثقب الأسود إلى الداخل خلال تكوينه، ولذلك فإن أي شيء يحدث داخل «أفق حدث» الثقب الأسود لا يمكن أن يؤثر على ما يحصل خارجه.

باستخدام هذه الخصائص الثلاثة الاساسية الخاصة بالثقب نفسه (الكتلة، الزخم الدوراني، الشحنة)، يمكن الاستدلال إلى أربعة أنواع من الثقوب السوداء بالاعتماد على نتائج حلول معادلة اينشتاين بالشكل التالي:

تمثل كل حالة حل مختلف لمعادلة المجال:

الشحنة / الزخم الدوراني غير دوراني (J = 0) دوراني (J > 0)
عدم وجود شحنة (Q = 0) شوارزشيلد كير
وجود شحنة (Q ≠ 0) رايسنر-نوردستروم كيرنيومان [الإنجليزية]

التكوين

تتشكل الثقوب السوداء الدوارة بطريقتين، إما من خلال الانهيار التثاقلي لنجم دوار هائل الكتلة أو بتصادم مجموعة من الاجسام أو النجوم أو سحب الغاز وتكون محصلة زخمها بعد التصادم لا تساوي صفراً، ولأن كل النجوم المعروفة في الفضاء هي نجوم دوارة وأن التصادمات بالواقع تملك محصلة زخم زاوي لاتساوي صفراً، فمن المتوقع أن تكون جميع الثقوب السوداء في الطبيعة هي ثقوب سوداء دوارة، ونظراً إلى أن الأجسام الفلكية المرصودة لا يمكن أن تمتلك شحنة كهربائية نقية، فإن حل الثقوب السوداء الدوارة في معادلة اينشتاين والمسمى بحل «كير» هو الوحيد الذي يمثل ظاهرة طبيعية حقيقة على علاقة بالفيزياء الفلكية، أما الحلول الأخرى تصف حالات افتراضية فقط.

في أواخر عام 2006، تمكن علماء الفلك من الحصول على تقديرات لمعدل دوران الثقوب السوداء ونشر عملهم في مجلة الفيزياء الفلكية، ومنها الثقب الأسود الموجود ضمن ثنائي (نجم-ثقب أسود) في مجرتنا درب التبانة والمسمى GRS 1915 + 105، والذي قد يملك معدل دوران حول نفسه يساوي 1150 مرة في الثانية الواحدة، [1] وهذا يقترب من الحدود النظرية العليا.

علاقة الدوران مع إنبعاثات اشعة غاما

يعتقد علمياً بأنه خلال مراحل تكوين الثقوب السوداء الدوارة عن طريق الإنهيار التثاقلي للنجم تتحرر اشعة عالية الطاقة بشكل إنبعاثات أشعة غاما انفجارية.

تفردية الثقب الأسود:

تسمى النقطة المركزية في قلب الثقب الأسود التي تتجمع فيها كافة كتلة الثقب «بنقطة التفرد»، في حالة الثقب الأسود الستاتيكي «عديم الدوران» تكون التفرد بشكل كرة متناهية في الصغر نصف قطرها يقترب أو يساوي صفراً، أما في حالة الثقوب السوداء الدوارة فتكون التفرد بشكل حلقة سمكها يساوي صفراً تسمى بالـ «التفرد الحلقي».

تحوّل ثقب كير الأسود إلى ثقب شفارزتشيلد

يمكن للثقب الأسود الدوار أن يحرر كميات كبيرة من الطاقة من خلال طاقته الدورانية، يحدث هذا من خلال عملية تسمى آلية بنروز في منطقة الإرغوسفير المحيطة بالثقب الأسود خارج أفق الحدث مباشرةً، ((بمعنى اخر: إذا تواجد أي جسم في هذه المنطقة فمن الممكن له ان يهرب بطاقة حركية أكبر من التي دخل فيها))، هنا يفقد الثقب الأسود طاقته الدورانية بشكل طاقة حركية للجسم القريب منه ويتباطأ دورانه متحولاً تدريجياً إلى ثقب شفارزتشيلد الأسود (ثقب أسود مستقر عديم الدوران) وهي ادنى حالة لثقب أسود لايمكنه بعدها أن يشع أو يملك طاقة دورانية، في كل الاحوال لايمكن لسرعة دوران ثقب كير الأسود أن تصل إلى الصفر.

مترية كير ومترية كير-نيومان

هناك حلان رياضيان وحيدان يمثلان ثقوب سوداء دوارة في معادلة آينشتاين للمجال يطلق عليهما متريات (أو مصفوفات)، كير و كير نيومان.

تغيّر الحالة الحرارية

يمكن ان توجد الثقوب السوداء الدوارة بحالتين حراريتين: ساخنة (فقدان الطاقة) وباردة. في عام 1989، أثبت العالم بول ديفيس أن الانتقال بين الحالتين يحدث عندما تساوي مربع كتلة الثقب الأسود مضاعفات معدل دورانه من النسبة الذهبية.[2]

هوامش

1. المحاور التناظرية تمثل المحاور التي تُقَسم الجسم إلى جزأين متشابهين تماماً.

انظر أيضاً

المراجع
  1. Black hole spins at the limit | COSMOS magazine نسخة محفوظة 14 نوفمبر 2018 على موقع واي باك مشين.
  2. Livio, Mario (22 أغسطس 2012)، "The Golden Ratio and Astronomy"، هافينغتون بوست، مؤرشف من الأصل في 10 يناير 2017، اطلع عليه بتاريخ 08 مايو 2019.

قراءات إضافية
  • C. W. Misner, K. S. Thorne, J. A. Wheeler, J. Wheeler, and K. Thorne, Gravitation (Physics Series), 2nd ed. W. H. Freeman, September 1973.
  • Macvey, John W., Time Travel, Scarborough House, 1990
  • Melia, Fulvio, The Galactic Supermassive Black Hole, Princeton U Press, 2007
  • بوابة الفيزياء
  • بوابة علم الفلك
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.