خلية ويغنر-سيتز
خلية ويغنر-سيتز (بالإنجليزية: Wigner–Seitz cell)، في فيزياء الحالة الصلبة هي خلية أولية يتم إنشاؤها بتطبيق تحليل فورونوي على الشبيكة البلورية لغرض دراسة هيئة بلورات المواد الصلبة، سميت نسبةً للعالمان يوجين ويغنر وفريدريك سيتز.
تملك البلورات خاصية فريدة، هي أن ذراتها مرتبة في مصفوفة منتظمة ثلاثية الأبعاد تسمى الشبيكة، كل الخصائص التي تتميز بها المادة الصلبة تعتمد على هذا الهيكل عالي الإنتظام الذي تظهر فيه خاصية التناظر الإنتقالي، ولأجل نمذجة ودراسة هذه الأنظمة الدورية فمن ضروري وجود أداة رياضية لوصف ذلك التناظر ومن ثم إطلاق الإستنتاجات حول خصائص المواد التي تنتج عنه، وخلية ويغنر-سيتز تمثل هذه الأداة.
خلية ويغنر-سيتز هي خلية أولية تحتوي على نقطة شبيكة منفردة، في الشبيكة الواحدة يوجد عدد لا يحصى من الخلايا الأولية المحتملة، ولكن يوجد شكل واحد فقط لخلية ويغنر-سيتز لكل شبيكة مختلفة.
التعريف
تعرف خلية ويغنر-سيتز حول نقطة شبيكة بأنها المنطقة التي تكون جميع النقاط داخلها أقرب ما يمكن إلى نقطة الشبيكة الأصلية من النقاط المجاورة لها أخرى ضمن الشبيكة نفسها.[1] رياضياً تحقق خلية ويغنر-سيتز صفة الخلية الأولية، هذا يعني أنها تمثل أصغر وحدة هندسية يمكنها أن تملأ حجم الشبيكة كاملاً من دون ترك أي ثغرة أو فجوة، تسمى هذه الخاصية الدورية (فسيفسائية).
أنشئت فكرة هذه الخلية أول مرة من قبل العالمين يوجين ويغنر وفريدريك سيتز في ورقة بحثية نشراها عام 1933، استخدما فيها هذا التحليل كحل لمعادلة شرودينغر للإلكترون الحر في عنصر الصوديوم.[2]
تشكيل الخلية
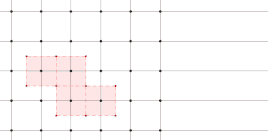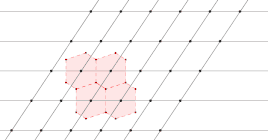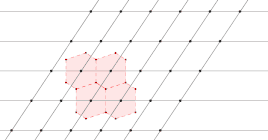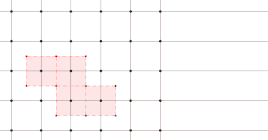
تمثل المساحة السداسية المحصورة داخل الخطوط الحمراء خلية ويغنر-سيتز المحيطة بنقطة الشبيكة المُعلمة باللون الأحمر.
المبدأ الأساسي الذي تقوم عليه خلية ويغنر-سيتز يعرف باسم خلية فورونوي، كما يطلق على تقسيمات خلايا فورونوي لمستوي يحتوي مجموعة من النقاط باسم مخطط فورونوي.

خطوات تشكيل الخلية في شبيكة ثنائية الأبعاد:
- إختيار إحدى نقاط الشبيكة كنقطة أصل لتحديد خلية ويغنر-سيتز حولها.
- يتم توصيل نقطة الأصل بمستقيمات إلى كافة النقاط المجاورة لها.
- ثم رسم خط عمودي عند منتصف كل من المستقيمات الواصلة بين نقطة الأصل والنقاط المحيطة.
- أقل مساحة محصورة بين تقاطعات الخطوط تمثل خلية ويغنر-سيتز حول نقطة الأصل.
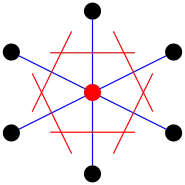
في الشبيكة الثلاثية الأبعاد:
- يتم رسم مستو عمودي على كل من المستقيمات التي تربط نقطة الشبيكة الأساسية بالنقاط المجاورة لها في الشبيكة.
- أصغر حجم محصور بين تقاطعات المستويات يمثل خلية ويغنر-سيتز لتلك الشبيكة.
عند تعميم شكل الخلية الناتج على النقاط المجاورة ستغطي كافة حجم الشبيكة دون ترك أي فاصل بينها.
يتم تحديد خلية ويغنر-سيتز التي تمثل الخلية الأولية للشبيكة من خلال اختبار كافة النقاط المجاورة لنقطة الخلية المستخدمة، لكن بشكل مختلف، في حالة تقليص متجهات الانتقال الأساسية للشبيكة بعملية إختزال الشبيكة [الإنجليزية]، فستظهر الحاجة لعدد معين من وحدات الخلية لغرض رسمها:[3]
في الفضاء ثنائي الأبعاد يجب استخدام نقاط الشبيكة الأربعة فقط التي تكّون أربع وحدات خلية مشتركة بالرأس في نقطة الأصل التي تمثل نقطة الشبيكة الأساسية، بينما في الفضاء ثلاثي الأبعاد تستخدم نقاط الشبيكة التي تكّون ثماني وحدات خلية مشتركة بالرأس في نقطة الأصل.
للشبيكات المركبة (التي تحتوي على متجهات انتقال أساسية مركبة بين الذرات) كل نقطة شبيكة منفردة ستمثل ذرة مختلفة هنا يمكن تقسيم خلية ويغنر-سيتز إلى خلايا ثانوية أصغر عن طريق تحليل فورونوي مرة أخرى لكن بالإعتماد على الذرات المشابهة الأقرب بدلاً من نقاط الشبيكة الأقرب، كما في تركيب كلوريد الصوديوم مثلاً.[4]


 تحديد خلية ويغنر-سيتز لنظام بلوري مكعب ممركز الجسم في الفضاء ثلاثي الأبعاد.
تحديد خلية ويغنر-سيتز لنظام بلوري مكعب ممركز الجسم في الفضاء ثلاثي الأبعاد.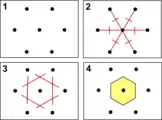 طريقة رسم خلية ويغنر-سيتز لشبيكة في الفضاء ثنائي الأبعاد.
طريقة رسم خلية ويغنر-سيتز لشبيكة في الفضاء ثنائي الأبعاد.
منطقة بريليون
نادراً ما تستخدم خلية ويغنر-سيتز عملياً في وصف الفضاء الحقيقي الشبيكة، عادةً تستخدم وحدات الخلية التقليدية بدلاً منها، ومع ذلك فإن التحليل الذي تقوم عليه هذه الخلية مهم جداً عند تطبيقه على الفضاء المقلوب، خلية ويغنر-سيتز في شبيكة مقلوبة تسمى منطقة بريليون وهي مهمة جداً كون من خلالها يمكن تحديد خصائص المادة الكهربائية والحرارية وغيرها.
طالع أيضاً
المراجع
- Solid state physics، Holt, Rinehart and Winston، 1976، ISBN 978-0-03-083993-1، مؤرشف من الأصل في 3 يونيو 2020.
- Wigner, E.؛ Seitz, F. (15 مايو 1933)، "On the Constitution of Metallic Sodium"، Physical Review (باللغة الإنجليزية)، 43 (10): 804–810، doi:10.1103/PhysRev.43.804، ISSN 0031-899X، مؤرشف من الأصل في 08 سبتمبر 2020.
- Hart, Gus L W؛ Jorgensen, Jeremy J؛ Morgan, Wiley S؛ Forcade, Rodney W (26 يونيو 2019)، "A robust algorithm for k-point grid generation and symmetry reduction"، Journal of Physics Communications، 3 (6): 065009، doi:10.1088/2399-6528/ab2937، ISSN 2399-6528، مؤرشف من الأصل في 17 مارس 2020.
- Solid state physics، San Diego: Academic Press، 2000، ISBN 978-0-08-048102-9، OCLC 162128885، مؤرشف من الأصل في 08 سبتمبر 2020.
- بوابة الفيزياء
- بوابة الكيمياء
- بوابة علم الأحجار الكريمة والمجوهرات
- بوابة علم المواد
- بوابة ميكانيكا الكم