خوارزمية أقليدس
في الرياضيات، خوارزمية أقليدس (بالإنجليزية: Euclidean algorithm) هي طريقة فعالة تمكن من إيجاد القاسم المشترك الأكبر لعددين وهو أكبر عدد يقسم في نفس الوقت العددين معا بدون أي باق من القسمة. يُرمز له بالفرنسية ب PGCD وبالإنجليزية GCD. سميت هذه الخوارزمية هكذا نسبة إلى عالم الرياضيات الإغريقي أقليدس الذي وصف الخوارزمية لأول مرة في كتابه المعروف باسم الأصول (حوالي عام 300 ق.م). هي مثال عن الخوارزميات (الخوارزمية طريقةٌ تمكن من القيام بعملية ما، خطوة خطوة طِبقا لقواعد معينة محددة مسبقا). وهو من أقدم الخوارزميات اللائي ما زلن قيد الاستعمال. قد تستعمل من أجل اختزال كسر إلى شكله المبسط غير القابل للاختزال، وهي جزء من الحسابات المتعلقة بنظرية الأعداد والتشفير.
خوارزمية أقليدس 
|

تعتمد خوارزمية أقليدس على مبدأ أن القاسم المشترك الأكبر لعددين لا يتغير إذا عُوض أكبرهما بالفرق بينه وبين أصغرهما.
الصيغة التي وُصفت أعلاه لخوارزمية أقليدس (وهكذا وصفها إقليدس) قد تتأخر أثناء عملية حساب الفرق بين أكبر العددين وأصغرهما، خصوصا إذا كان العدد الأكبر أكبر بكثير من العدد الأصغر. هناك صيغة أكثر سرعة من هذه الصيغة، تمكن من اختصار هذه المراحل. بدلا من تعويض أكبر العددين بالفرق بينه وبين أصغر العددين، يُعوض أكبر العددين بباقي قسمته على أصغر العددين. في هذه الطريقة، الخوارزمية تتوقف عندما يصيرا الباقي مساويا للصفر.
مثال
القاسم المشترك الأكبر ل 48 و 60 هو 12.
القاسم المشترك الأكبر للعددين 252 و 198:
252 = 198 * 1 + 54 ‘ أربع وخمسون هو باقي قسمة 252 على 198
فنجد القاسم المشترك للعددين 198 و 54
198 = 54 * 3 + 36 ‘ ست وثلاثون هو باقي القسمة.
نكرر العملية هذه المرة مع : 54 و 36
54 = 36 * 1 + 18
مرة أخرى : 36 = 18 * 2 + 0
هنا وصلنا للصفر فيكون العدد الثاني 18 هو القاسم المشترك الأكبر.
الخلفية : القاسم المشترك الأكبر
وصف الخوارزمية
القاسم المشترك الأكبر لعددين طبيعيين A، B يساوي القاسم المشترك الأكبر للعدد الثاني B وباقي قسمة A على B، ونكرر العملية نفسها حتى يصبح باقي القسمة مساويا الصفر، عندئذ يكون القاسم المشترك الأكبر هو العدد الآخر. حيث r هو باقي قسمة A على B.
N هو القاسم المشترك الأكبر.
التطور التاريخي

خوارزمية أقليدس هي واحدة من أقدم الخوارزميات الجارية الاستعمال. ظهرت في كتاب الأصول لإقليدس (في حوالي عام 300 قبل الميلاد).
تطبيقات رياضياتية
متطابقة بيزو
تنص متطابقة بيزو على أن القاسم المشترك الأكبر g لعددين a و b يمكن أن يمثل مجموعا خطيا للعددين a و b؛ أي أنه يوجد عددان، s و t حيث يتوفر ما يلي:
الخوارزمية الإقليدية الممتدة
یمكن تمثیل القاسم المشترك الأكبر للعددین عن طریق دمج خطي مع عددین آخرین،
كیف یمكن أیجاد قیمتي n و m وذلك عن طریق خوارزمیة اقلیدس الممتدة وهناك ثلاثة طرق لمعرفة هذه القیم (الطرق هي مشابه لبعض، لكن یمكن القول أنها مختصره من الأخریات). الطريقة الأولى: وهي يمكن ان نطلق عليها التراجع وفي هذه الطريقة نقوم بالحل عن طريق خوارزمية اقليدس وبعدها تقول بالتراجع الخلفي لايجاد قيمتي m،n كما في المثال التالي: مثال: قم بتمثيل العددين 26 و 21 بطريقة اقليدس الممتدة : فنبدأ بالحل كما هو الحال في طريقة اقليدس : 26 = 1* 21 + 5 و 21 = 4 * 5 + 1 و 5 = 5 * 1 + 0 وتتوقف عند الصفر. الآن المعادلة التي قبل المعادلة التي باقيها صفر أي المعادلة الثانية نقوم بكتابتها بالشكل التالي :
أیضا المعادلة الأولى بنفس الشكل :
في المعادلتين السابقتين
- 1 = 21 – 4 * (26 – 1 * 21)
ومن غیر أجراء عملیة حسابیة، فقط نفك القوس لینتج : 1 = 21 -4*26 +4*21 1=21(1+4)-4*26 حيث 21 عامل مشترك لیكون لدینا الناتج النهائي : 4*21 +21
1 = 5*21 + (-4)*26 نتاكد من النتيجة 5*21+ -4*26 والناتج يساوي واحد إذاً المعادلة صحيحة
إذاً قيمة m هي 5 وقيمة n هي -4.
المعادلات الديوفانتية الخطية
يمكن لخوارزمية أقليدس أيضا أن تستعمل من أجل حلحلة العديد من المعادلات الديوفانتية الخطية. تظهر واحدة من هده المعادلات في مبرهنة الباقي الصيني.
شجرة ستيرن-بروكوت
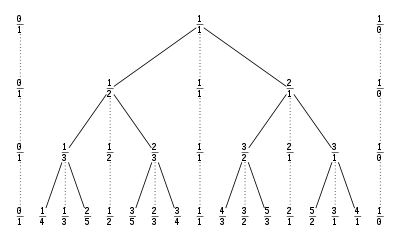
انظر شجرة ستيرن-بروكوت.
الفعالية الخوارزمية

دُرست فعالية خوارزمية أقليدس بشكل كثيف. تتمثل هذه الفعالية في عدد الخطوات اللازمة من أجل إيجاد القاسم المشترك الأكبر المراد حسابه. أول تحليل لفعالية الخوارزمية يرجع إلى العالم غيينو، (كان ذلك عام 1811)، حيث أثبت أنه أثناء حساب القاسم المشترك الأكبر للعددين u و v، عدد الخطوات اللازمة، لا يمكن أن يتجاوز v. وزاد فيما بعد هذا البرهانَ دقة عندما برهن أن هذا العدد لا يمكن أن يتجاوز v/2 +2.
انظر إلى بيير جوزيف إتيان فينك وإلى إيميل ليجي وإلى غابرييل لامي.
في النظم العددية الأخرى
الأعداد الطبيعية الغاوسية

الأعداد الغاوسية الصحيحة هن أعداد مركبة α = u + vi حيث u و v أعداد صحيحة.
تعميمات إلى بُنى رياضياتية أخرى

مراجع
- من كتاب مقدمة في التشفير بالطرق الكلاسيكية
وصلات خارجية
- بوابة خوارزميات
- بوابة رياضيات
- بوابة علم الحاسوب
- بوابة نظرية الأعداد